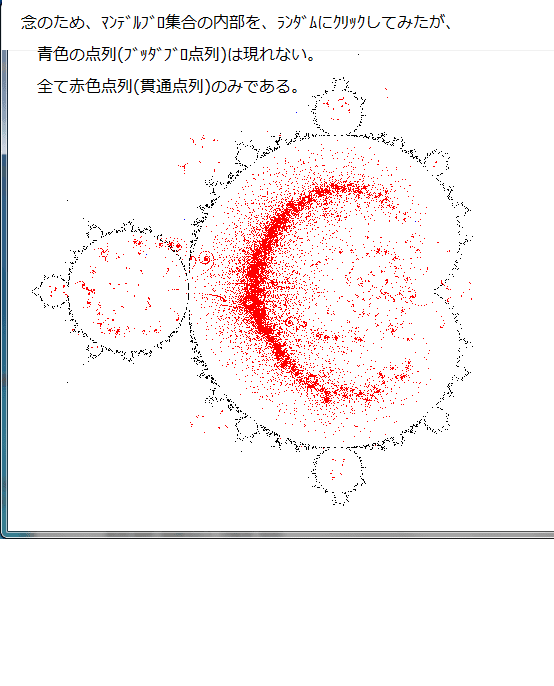
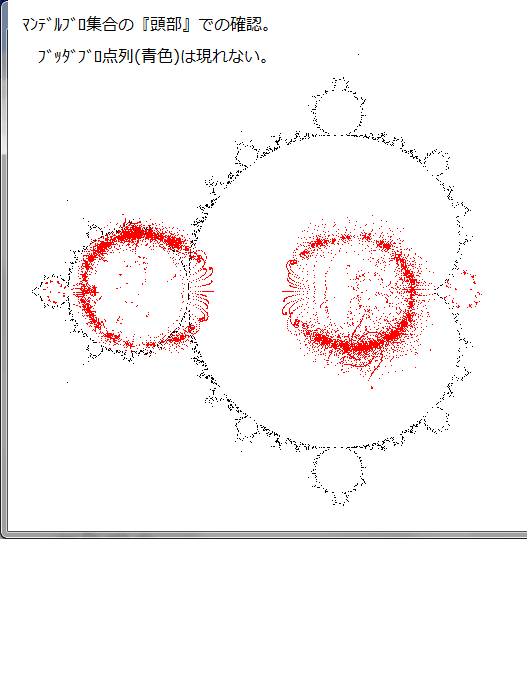
Z^2マンデルブロ集合の点座標を始点とした点列に、ブッダブロ点列が現れるか否か、再度、マウス・クリックで再確認した。始点をマウスでクリックして与える方法である。点列が青色になればブッダブロ点列である。赤色になれば貫通点列である。マンデルブロ集合の『尻』部分にブッダブロ点列が現れることは前より分かっていた。そこで、その確認もした。以下の結果の画像である。


---------------------------------------------------
記事264の結果(マンデルブロ集合の点を始点とする点列にブッダブロ点列が存在すること)と上図の一番上の図とは矛盾はしていない。マンデルブロ集合座標の『尻』部分の座標値を始点とする点列は確かにブッダブロ点列となっている。しかし、これはどうも納得できない。
そこで初めに戻って少し整理てみよう。私は何か勘違いていないか。
***
いま、複素平面において画像を表示したい複素座標をD(X,Y)とする。Xは実軸上の値、Yは虚軸上の値とする。ここで、Dの中の点Z(X,Y)とし、次の巡回式を考える。
巡回式: Z(X,Y)←Z(X,Y)^2+Z0(X0,Y0)・・・・・・・・・・・・・・(1)
ここでZ0(X0,Y0)はD内の固定値(定数)とする。
また変数:X,Yの初期値は共に0とする。
また巡回式の最大巡回回数も決めておき、それをNmaxとする。
***
X,Yの初期値は共に0だから、Z(X,Y)^2=0 故、(1)より複素平面上に以下の点列が得られる。
Z0,Z1,Z2,・・・・,ZNmax・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
***
マンデルブロ集合とは、Nmax→∞の場合でも『発散しない』ような点Z0の集合である。
***
ここで、(2)の点列で、|Zn|=(X^2+Y^2)^0.5>2 ・・・・・・(3)
となったとしよう。その場合は『発散した』とする。
***
そこでマンデルブロ集合とは、(3)を満足しないD内の点Z0の集合とする。
( ここで、(2)の点列を新たに求めるときは、即ち、Z0を変える場合は、
変数:X,Yの初期値は0にする。)
***
次に、ブッダブロ点列とは、以下のように定義する。
点列(2)が、Znで(3)を満足したとき、以下の点列をブッダブロ点列とする。
Z0,Z1,Z2.・・・,Zn・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
***
ブッダブロ集合とは、(4)となるD内の全ての点Z0の集合:Aとする。
ブッダブロ画像とは、Aの全ての点列(4)の集合画像を言うものとする。
***
貫通点列とは、以下のように定義する。
点列(2)において、(3)を満足しないとき、(2)の点列を貫通点列と定義する。
貫通集合とは、(2)となるD内の全ての点Z0の集合:Bとする。
貫通画像とは、Bの全ての点列(2)の集合画像とする。
-----------------------------------------------------------------------
上の定義からすれば、マンデルブロ集合を始点とする点列は貫通点列しか存在しえない。
しかし画像結果は『マンデルブロ集合を始点とする点列にブッダブロ点列が存在していた。
のみならず、その点列集合は明らかにブッダブロ画像となっていた→記事295の結果。
ということは、結局、私の画像作成プログラムにバグというよりプロミングミスがあることしか考えられない。
****
記事292,293の『マンデルブロ集合の縁(ふち)の画像』結果については上記した点列定義と矛盾していない。
問題があるとしたら、記事295の、マンデルブロ集合との与え方と、それによる点列画像プログラムに不具合があることしか考えられない。




---------------------------------------------------
記事264の結果(マンデルブロ集合の点を始点とする点列にブッダブロ点列が存在すること)と上図の一番上の図とは矛盾はしていない。マンデルブロ集合座標の『尻』部分の座標値を始点とする点列は確かにブッダブロ点列となっている。しかし、これはどうも納得できない。
そこで初めに戻って少し整理てみよう。私は何か勘違いていないか。
***
いま、複素平面において画像を表示したい複素座標をD(X,Y)とする。Xは実軸上の値、Yは虚軸上の値とする。ここで、Dの中の点Z(X,Y)とし、次の巡回式を考える。
巡回式: Z(X,Y)←Z(X,Y)^2+Z0(X0,Y0)・・・・・・・・・・・・・・(1)
ここでZ0(X0,Y0)はD内の固定値(定数)とする。
また変数:X,Yの初期値は共に0とする。
また巡回式の最大巡回回数も決めておき、それをNmaxとする。
***
X,Yの初期値は共に0だから、Z(X,Y)^2=0 故、(1)より複素平面上に以下の点列が得られる。
Z0,Z1,Z2,・・・・,ZNmax・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)
***
マンデルブロ集合とは、Nmax→∞の場合でも『発散しない』ような点Z0の集合である。
***
ここで、(2)の点列で、|Zn|=(X^2+Y^2)^0.5>2 ・・・・・・(3)
となったとしよう。その場合は『発散した』とする。
***
そこでマンデルブロ集合とは、(3)を満足しないD内の点Z0の集合とする。
( ここで、(2)の点列を新たに求めるときは、即ち、Z0を変える場合は、
変数:X,Yの初期値は0にする。)
***
次に、ブッダブロ点列とは、以下のように定義する。
点列(2)が、Znで(3)を満足したとき、以下の点列をブッダブロ点列とする。
Z0,Z1,Z2.・・・,Zn・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
***
ブッダブロ集合とは、(4)となるD内の全ての点Z0の集合:Aとする。
ブッダブロ画像とは、Aの全ての点列(4)の集合画像を言うものとする。
***
貫通点列とは、以下のように定義する。
点列(2)において、(3)を満足しないとき、(2)の点列を貫通点列と定義する。
貫通集合とは、(2)となるD内の全ての点Z0の集合:Bとする。
貫通画像とは、Bの全ての点列(2)の集合画像とする。
-----------------------------------------------------------------------
上の定義からすれば、マンデルブロ集合を始点とする点列は貫通点列しか存在しえない。
しかし画像結果は『マンデルブロ集合を始点とする点列にブッダブロ点列が存在していた。
のみならず、その点列集合は明らかにブッダブロ画像となっていた→記事295の結果。
ということは、結局、私の画像作成プログラムにバグというよりプロミングミスがあることしか考えられない。
****
記事292,293の『マンデルブロ集合の縁(ふち)の画像』結果については上記した点列定義と矛盾していない。
問題があるとしたら、記事295の、マンデルブロ集合との与え方と、それによる点列画像プログラムに不具合があることしか考えられない。



















