Z^n+C 画像(但しn=正整数、C=実定数)画像例を以下に示す。
1図
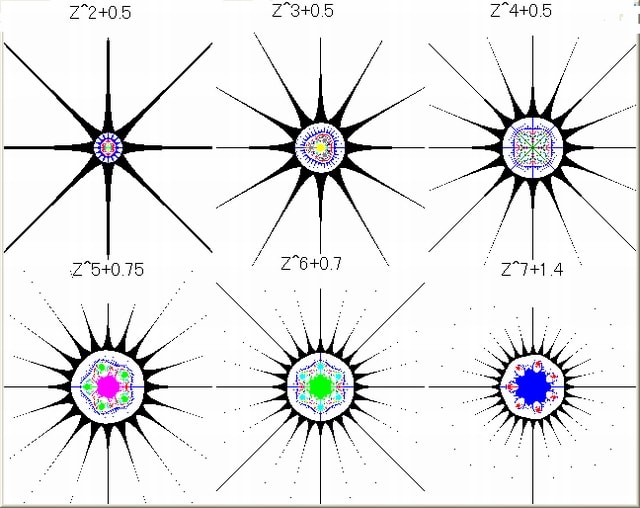
2図

3図

2図は1図の拡大図(「内臓部」)である。
----------------------------------------------
これらの図の画像作成条件の概略は以下のとおり。
1.N-loop脱出条件:X^2+Y^2>100
2.pset条件:|X|<10 or |Y|<10
3.色:C=No mod 16 (NoはN-loop脱出時のN値)
----------------------------------------------
上図から分かるように『Z^n+C (n:正整数 ,C:実数)の画像は『同形なn個の画像から構成されている。』
この『・・・』の命題が正しければ、このような画像の分析は、n個のうちの1つの画像を調べれば其の調査結果は其の画像全体についての結果になる。 この記事の後で、ちょっとした画像分析をしたいと思っているので、『・・・』が正しいかどうかを調べる。
この程度の問題なら私でも解けそうだ。そこで、昔々の学生時代を偲びつつ証明しよう。
-----------------------------------------
[命題]
『nが正整数、Cが実定数のとき、複素関数:Z^n+Cの“放散虫”の画像は、原点を中心とした扇状にn分割された各領域で、同一な画像から成立している。』
[証明]
複素平面を原点(0,0)を中心として扇状に、同じ大きさにn分割する。第1番目の分割領域内の点(X,Y)を極座標表(R,θ)表示すると、Z=X+iY=R*e^iθとなる。ここで、R=(X^2+Y^2)^0.5, θ=arctan(Y/X)である。
次に、任意の正整数をm ( < n ) とし、第m番目の分割領域について考える。 Rを一定値にしてθを(2π/n)*m (radian) 回転させると、点(X,Y)は、第m番目の分割領域に移動する。その点を(Xm,Ym)とすると、その点は、Z=Xm+iYm=R*e^i(θ+(2*π/n)*m)となる。
ここで、Z^nを、分割領域1及び分割領域mについて求めてみる。
分割領域1では、Z=R^n*e^i(n*θ)となる。
次に分割領域mでは、Z=(R*e^i(θ+(2*π/n)*m))^n=(R^n)*(e^i((θ+2*π/n)*m*n)=(R^n)*(e^i(n*θ))*e^(i*m*2*π) = (R^n)*e^i(n*θ)(cos(2*m*π)+i*sin(2*m*π)=(R^n)*e^i(n*θ)となり、領域1でのZ^nと一致する。
(注:cos(2*m*π)=1, sin(2*m*π)=0)
従って、Rを固定値としたとき、領域1と領域mでのZ^n値は全く一致するため、それらの領域での、点(X,Y)と点(Xm,Ym)の挙動は全て一致する。故に、これらの挙動の結果生ずる、任意の条件化下の図形表示は、n分割された領域のそれぞれで、全て一致することになる。
(補足:画像全体の作成手順の概要は、始めRを初期値に固定しθ=0→2πと変化させて計算し、次にRを次の値に固定し、θ=0→2πと変化させて計算する。これを繰り返す)
以上より、複素関数:Z^n+C の図形は、原点を中心としてn分割された領域で、全く同一の画像から構成されることになる。
(証明終り)
なお、この証明の正しさを確認するため、Z^3の場合について、N-loopの入出力での点(X,Y)の軌跡を調べた。その件については、このブログの後の記事で掲載する予定。



















