音の伝搬をリープフロッグアルゴリズムにる時間発展の式に落とすと次のようになる。[3]
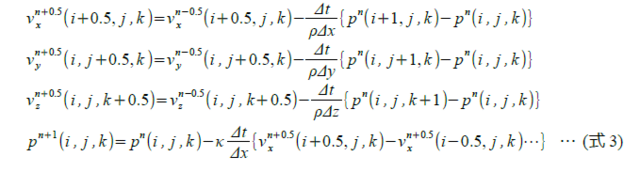 …式3
…式3
これに安直にabsorption coefficients σ を適用すると次のようになる
 …式4
…式4
σの値は、基本的に関心領域では0であり、PML層を外側に向かって多項式(polynominal)に増加させる。[1]
PML層の外側の境界条件は例えば剛な境界とする。

Fig. 1 Yee cell と σ
ここで、PMLを何層とするか、σをどのような関数にするかが問題となる。
関心領域から距離をd、PML層の厚さをdPMLとしたとき、σを次のようなM次関数とすることが提唱されている[4]が、これでもなお乗数MとσMAXの値に任意性がある。
 …式5
…式5
[1] Ludovic Métivier, Laurence Halpern. Perfectly Matched Layers equations for 3D acoustic wave propagation in heterogeneous media. WAVES 2011, Jul 2011, Vancouver, Canada. ⟨hal-00826617⟩
[2] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p12-14
[3] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p9-10
[4] 宇野 亨編著 何 一偉, 有馬 卓司 共著、数値電磁界解析のためのFDTD法 -基礎と実践-、コロナ社(2016)
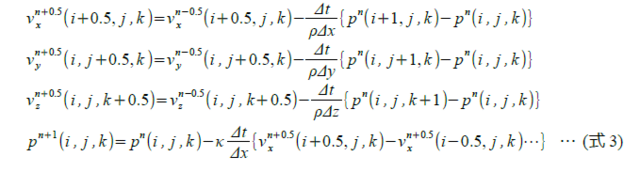 …式3
…式3これに安直にabsorption coefficients σ を適用すると次のようになる
 …式4
…式4σの値は、基本的に関心領域では0であり、PML層を外側に向かって多項式(polynominal)に増加させる。[1]
PML層の外側の境界条件は例えば剛な境界とする。

Fig. 1 Yee cell と σ
ここで、PMLを何層とするか、σをどのような関数にするかが問題となる。
関心領域から距離をd、PML層の厚さをdPMLとしたとき、σを次のようなM次関数とすることが提唱されている[4]が、これでもなお乗数MとσMAXの値に任意性がある。
 …式5
…式5[1] Ludovic Métivier, Laurence Halpern. Perfectly Matched Layers equations for 3D acoustic wave propagation in heterogeneous media. WAVES 2011, Jul 2011, Vancouver, Canada. ⟨hal-00826617⟩
[2] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p12-14
[3] 豊田正弘 編著. FDTD法で視る音の世界, コロナ社 (2015), p9-10
[4] 宇野 亨編著 何 一偉, 有馬 卓司 共著、数値電磁界解析のためのFDTD法 -基礎と実践-、コロナ社(2016)


















