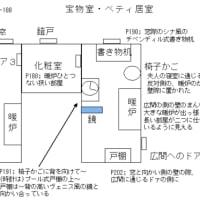
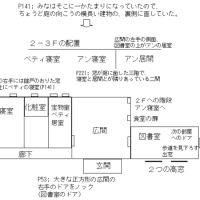
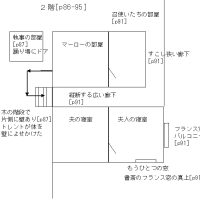
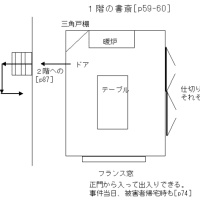
前回からの続き
ではゲーデルの対角化定理の証明に入ります。以下の証明は簡単と言えば簡単ですっきりしていますが、論理式、そのゲーデル数、その自然数を記述する記号や式、その記号や式のゲーデル数、とまあ色々複雑な関係が出てきますから、そこの絡みをキチンと見分けないと混乱します。
【再掲】ゲーデルの対角化定理(前原の定理8.3,Ref-3-p130)
任意の1変数論理式R(x)について、次の式を満たす確定文Aが存在する。
式4.1-1 A⇔R(a) ただしa=~A~
まず、1変数述語式A(x)と、その変数記号xに対象項tを代入した確定文A(t)を考えます。そして、前3者のゲーデル数a,b,cから確定文A(t)のゲーデル数kを返す関数Sb(a,b,c)を考えます。これはxをaで置換(Substitute)したときのゲーデル数を返す関数といった意味を持つので"Substitute"の頭文字から記号を付けています。
関数定義4.3-1a Sb(a,b,c)の値kは、
a=~A(x)~、b=~x~、c=~t~ のとき、k=~A(t)~
それ以外のとき k=0
この関数は論理式で表現されますが、証明は複雑なので後回しにします。また変数記号xは形式的体系で用意されているどの変数記号でも構いませんが、以下の議論の間は固定しておけますし、その間はb=~x~も固定できますから、bは以後省略した表記を使います。つまり2変数関数として考えます。
関数定義4.3-1b Sb(a,c)の値kは、
a=~A(x)~、c=~t~ のとき、k=~A(t)~
それ以外のとき k=0
このSb関数は表現可能で、次の命題が成り立ちます。
命題4.3-1a a=~A(x)~、c=~t~ のとき、Sb(a,c)=kなるkが存在し、有限の手順でkを得ることができる。
命題4.3-1b このとき、Sb(a,c)=kはペアノ公理系で証明できる
命題4.3-1aはSb関数の定義から明らかで、単に~A(t)~を求めるだけの手続きです。まるで言うまでもないことに見えますが、きちんと明示しておくと後に何かと便利なのです。命題4.3-1bは前述の通り、証明は少し複雑です。
さてtには対象式、つまりなんらかの自然数を記述する式(定数記号か関数式)が当てはめられますが、ここでtを、自然数nを記述する定数記号nに限定します*1。そしてc=~n~を次のような関数Z(n)に置き換えます。
関数定義4.3-2 Z(n)の値cは、 c=~n~
すると任意の1変数述語式A(x)と任意の自然数nについて次の命題が成り立ちます。
命題4.3-2a a=~A(x)~ のとき、Sb(a,Z(n))=kなるkが存在し、有限の手順でkを得ることができる。k=~A(n)~ 。
命題4.3-2b このとき、 |--- Sb(a,Z(n))=k
ここでn=a=~A(x)~とおけば、任意の自然数1変数述語式A(x)について次の命題が成り立ちます。後述のように、このn=aとおく手法が対角化と呼ばれる所以です。
命題4.3-3a a=~A(x)~ のとき、Sb(a,Z(a))=kなるkが存在し、有限の手順でkを得ることができる。k=~A(a)~ 。
命題4.3-3b このとき、 |--- Sb(a,Z(a))=k
ここまで準備したところで任意の1項関係R(x)を考えます。任意の1項関係R(x)について、おなじ数を代入した命題は同値なので次の命題が成り立ちます。ここでA(a)も任意です。
命題4.3-4a R(Sb(a,Z(a)))⇔R(k) が成り立つ
a=~A(x)~ 、Z(a)=~a~ 、k=~A(a)~
命題4.3-4b |--- R(Sb(a,Z(a)))⇔R(k)
ここでA(x)をR(Sb(x,Z(x)))とおくと、A(x)のゲーデル数gとA(g)のゲーデル数kとの間に次の関係が成り立ち、この関係が論理式で表現されます。
命題4.3-4 Sb(g,Z(g))=k が成立し、 |--- Sb(g,Z(g))=k
命題4.3-5 R(Sb(g,Z(g)))⇔R(k) が成立し、 |--- R(Sb(g,Z(g)))⇔R(k)
g=~R(Sb(x,Z(x)))~ 、Z(g)=~g~ 、k=~R(Sb(g,Z(g)))~
確定文A(g)をAとすれば命題4.3-5の式R(Sb(g,Z(g)))⇔R(k)はすなわちA(g)⇔R(~A(g)~)であり、式4.1-1になります。すなわち、任意の1変数論理式R(x)についてゲーデルの対角化定理を満たす確定文Aとは、上記のR(Sb(g,Z(g)))のことだったのです。
ここで対角化と呼ばれる所以を図で示します。
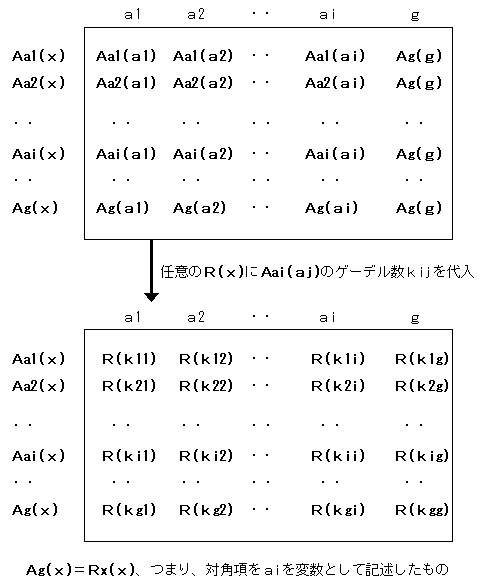
この図の上の行列は、縦には全ての1変数論理式A[ai](x)を順番に並べ、横にはそのゲーデル数aiを並べたものです。例えばゲーデル数の小さい順に並べれば、これは可能です。そして行列の中には、各行の論理式A[ai](x)に、各列の自然数ajを代入した確定文A[ai](aj)が位置します。ここで各座標の確定文A[ai](aj)のゲーデル数をkijとすれば、
kij=Sb(a,c)、a=~A[ai](x)~、c=~aj~
そして、この行列の対角成分は確定文A(~A(x)~)、すなわち1変数論理式A(x)に自身のゲーデル数を代入した確定文になっています。
下の行列には、上の行列の各座標の任意の確定文A[ai](aj)のゲーデル数kijを任意の1変数論理式R(x)に代入した確定文R(kij)が並んでいます。そして下の行列の対角成分は各列の自然数ajと1対1対応しているので、ゲーデル数ajを変数とした1変数関数Ag(x)の値になります。そしてAg(x)が1変数論理式Ag(x)で記述できたならば、そのAg(x)は縦に並んだ全ての1変数論理式A[ai](x)のどこかに存在しているはずです。するとAg(x)にそのゲーデル数gを代入した確定文Ag(g)が、自身もその否定も証明できない論理式となります。
実数濃度が自然数濃度より大きいことを証明するカントールの対角線論法では、対角線上の要素から作り出した数がどの列にも存在しないことを示したのですが、ゲーデルの対角化定理では、対角線上の要素から作り出した論理式もどこかの列に存在することを利用している、というわけです。
ここで下の行列の対角線を表す関数Ag(x)を表現する論理式Ag(x)が存在することを証明しなくてはなりません。すなわち、これまで積み残してきた、Sb(a,b,c)、Z(n)、B(y,x)を表現する論理式の存在証明が必要です。これは長い証明を経ずに的確に説明する自信がありませんので、興味のある方は参考文献などを御参照ください。要領としては基本的な関数の表現可能性からコツコツと積み上げる感じです。
ひとまずこれにて、第1不完全性定理の証明の話を終わります。
-------
*1) 実際には1個の定数記号でなくてもよく、ゲーデルの定理-2.3- 自然数の公理系で示したように、s(s・・・(s(0)・・・))や0''・・・''のような後者関数を使った記号列でもよい。要は自然数と1対1対応している記号や記号列であれば関数Z(n)が定義できるのである。
ではゲーデルの対角化定理の証明に入ります。以下の証明は簡単と言えば簡単ですっきりしていますが、論理式、そのゲーデル数、その自然数を記述する記号や式、その記号や式のゲーデル数、とまあ色々複雑な関係が出てきますから、そこの絡みをキチンと見分けないと混乱します。
【再掲】ゲーデルの対角化定理(前原の定理8.3,Ref-3-p130)
任意の1変数論理式R(x)について、次の式を満たす確定文Aが存在する。
式4.1-1 A⇔R(a) ただしa=~A~
まず、1変数述語式A(x)と、その変数記号xに対象項tを代入した確定文A(t)を考えます。そして、前3者のゲーデル数a,b,cから確定文A(t)のゲーデル数kを返す関数Sb(a,b,c)を考えます。これはxをaで置換(Substitute)したときのゲーデル数を返す関数といった意味を持つので"Substitute"の頭文字から記号を付けています。
関数定義4.3-1a Sb(a,b,c)の値kは、
a=~A(x)~、b=~x~、c=~t~ のとき、k=~A(t)~
それ以外のとき k=0
この関数は論理式で表現されますが、証明は複雑なので後回しにします。また変数記号xは形式的体系で用意されているどの変数記号でも構いませんが、以下の議論の間は固定しておけますし、その間はb=~x~も固定できますから、bは以後省略した表記を使います。つまり2変数関数として考えます。
関数定義4.3-1b Sb(a,c)の値kは、
a=~A(x)~、c=~t~ のとき、k=~A(t)~
それ以外のとき k=0
このSb関数は表現可能で、次の命題が成り立ちます。
命題4.3-1a a=~A(x)~、c=~t~ のとき、Sb(a,c)=kなるkが存在し、有限の手順でkを得ることができる。
命題4.3-1b このとき、Sb(a,c)=kはペアノ公理系で証明できる
命題4.3-1aはSb関数の定義から明らかで、単に~A(t)~を求めるだけの手続きです。まるで言うまでもないことに見えますが、きちんと明示しておくと後に何かと便利なのです。命題4.3-1bは前述の通り、証明は少し複雑です。
さてtには対象式、つまりなんらかの自然数を記述する式(定数記号か関数式)が当てはめられますが、ここでtを、自然数nを記述する定数記号nに限定します*1。そしてc=~n~を次のような関数Z(n)に置き換えます。
関数定義4.3-2 Z(n)の値cは、 c=~n~
すると任意の1変数述語式A(x)と任意の自然数nについて次の命題が成り立ちます。
命題4.3-2a a=~A(x)~ のとき、Sb(a,Z(n))=kなるkが存在し、有限の手順でkを得ることができる。k=~A(n)~ 。
命題4.3-2b このとき、 |--- Sb(a,Z(n))=k
ここでn=a=~A(x)~とおけば、任意の自然数1変数述語式A(x)について次の命題が成り立ちます。後述のように、このn=aとおく手法が対角化と呼ばれる所以です。
命題4.3-3a a=~A(x)~ のとき、Sb(a,Z(a))=kなるkが存在し、有限の手順でkを得ることができる。k=~A(a)~ 。
命題4.3-3b このとき、 |--- Sb(a,Z(a))=k
ここまで準備したところで任意の1項関係R(x)を考えます。任意の1項関係R(x)について、おなじ数を代入した命題は同値なので次の命題が成り立ちます。ここでA(a)も任意です。
命題4.3-4a R(Sb(a,Z(a)))⇔R(k) が成り立つ
a=~A(x)~ 、Z(a)=~a~ 、k=~A(a)~
命題4.3-4b |--- R(Sb(a,Z(a)))⇔R(k)
ここでA(x)をR(Sb(x,Z(x)))とおくと、A(x)のゲーデル数gとA(g)のゲーデル数kとの間に次の関係が成り立ち、この関係が論理式で表現されます。
命題4.3-4 Sb(g,Z(g))=k が成立し、 |--- Sb(g,Z(g))=k
命題4.3-5 R(Sb(g,Z(g)))⇔R(k) が成立し、 |--- R(Sb(g,Z(g)))⇔R(k)
g=~R(Sb(x,Z(x)))~ 、Z(g)=~g~ 、k=~R(Sb(g,Z(g)))~
確定文A(g)をAとすれば命題4.3-5の式R(Sb(g,Z(g)))⇔R(k)はすなわちA(g)⇔R(~A(g)~)であり、式4.1-1になります。すなわち、任意の1変数論理式R(x)についてゲーデルの対角化定理を満たす確定文Aとは、上記のR(Sb(g,Z(g)))のことだったのです。
ここで対角化と呼ばれる所以を図で示します。
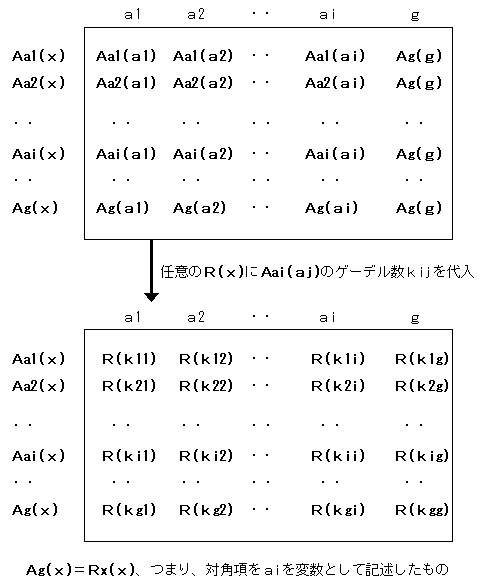
この図の上の行列は、縦には全ての1変数論理式A[ai](x)を順番に並べ、横にはそのゲーデル数aiを並べたものです。例えばゲーデル数の小さい順に並べれば、これは可能です。そして行列の中には、各行の論理式A[ai](x)に、各列の自然数ajを代入した確定文A[ai](aj)が位置します。ここで各座標の確定文A[ai](aj)のゲーデル数をkijとすれば、
kij=Sb(a,c)、a=~A[ai](x)~、c=~aj~
そして、この行列の対角成分は確定文A(~A(x)~)、すなわち1変数論理式A(x)に自身のゲーデル数を代入した確定文になっています。
下の行列には、上の行列の各座標の任意の確定文A[ai](aj)のゲーデル数kijを任意の1変数論理式R(x)に代入した確定文R(kij)が並んでいます。そして下の行列の対角成分は各列の自然数ajと1対1対応しているので、ゲーデル数ajを変数とした1変数関数Ag(x)の値になります。そしてAg(x)が1変数論理式Ag(x)で記述できたならば、そのAg(x)は縦に並んだ全ての1変数論理式A[ai](x)のどこかに存在しているはずです。するとAg(x)にそのゲーデル数gを代入した確定文Ag(g)が、自身もその否定も証明できない論理式となります。
実数濃度が自然数濃度より大きいことを証明するカントールの対角線論法では、対角線上の要素から作り出した数がどの列にも存在しないことを示したのですが、ゲーデルの対角化定理では、対角線上の要素から作り出した論理式もどこかの列に存在することを利用している、というわけです。
ここで下の行列の対角線を表す関数Ag(x)を表現する論理式Ag(x)が存在することを証明しなくてはなりません。すなわち、これまで積み残してきた、Sb(a,b,c)、Z(n)、B(y,x)を表現する論理式の存在証明が必要です。これは長い証明を経ずに的確に説明する自信がありませんので、興味のある方は参考文献などを御参照ください。要領としては基本的な関数の表現可能性からコツコツと積み上げる感じです。
ひとまずこれにて、第1不完全性定理の証明の話を終わります。
-------
*1) 実際には1個の定数記号でなくてもよく、ゲーデルの定理-2.3- 自然数の公理系で示したように、s(s・・・(s(0)・・・))や0''・・・''のような後者関数を使った記号列でもよい。要は自然数と1対1対応している記号や記号列であれば関数Z(n)が定義できるのである。
















※コメント投稿者のブログIDはブログ作成者のみに通知されます