前回(2018-04-09)の続きです。
今度は膨張宇宙の地平線の話です。これについては一般相対性理論の教科書、例えば[Ref-1])などに書かれていますが、前回も紹介したEMANの相対性理論の「ロバートソン・ウォーカー計量」から「膨張宇宙では粒子は減速する」などにも書かれています。
まずはビッグバンの前、宇宙が小さかった時から出発しましょう。ここで宇宙は正の曲率で曲がっていた、つまり4次元球面であったとします。その方が次の点で考えやすいからです。
・平坦だったとすると無限でなければ境界があることになりややこしい。
・極めて高密度だから重力で歪んでいたはずで、平坦だったとは考えにくい。
4次元球面というのはイメージすることが難しいので、普通の3次元球面、例えば膨張する風船の表面でイメージすることにしましょう。ビッグバンが始まった時、もっと言えばインフレーションが起きた時、宇宙の中の各点は相互に急激な加速度運動を行い、ひとつの点から見るとある距離以上の点は地平線の向こうへと消えたのです。まあ最初の時点は置いといて、一定の速度で膨張しているというモデルで考えます。これを4次元球の2次元断面として示すと図のようになります。
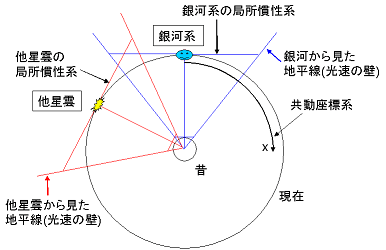
この図で4次元球面である宇宙全体に張られた座標は共動座標系と呼ばれます。星雲の運動と同時に動く座標系という意味です。それに対して各星雲や我等が銀河系に固定された慣性系は4次元球面に接する平坦な接3次元空間になります。この慣性系は星雲近傍の空間だけを近似的に表せるだけであり、宇宙全体を表すことはできません。ゆえに局所慣性系と呼ばれます。逆に言うと宇宙全体は慣性系ではありません。すると宇宙全体には特殊相対性理論は成り立たなくてもよくて光速を越えてはいけないという限界もなくなります。具体的には、ある距離以上の星雲は銀河から光速以上で遠ざかっていてもいい、ということになり、それらの星雲からの光は永久に我等が銀河系には届きません。
さてそうすると、「原理的に観測不可能、つまり実地検証のできない事について述べることは科学的に意味のあることなのか?」という疑問が生まれるかも知れません。宇宙の地平線の向こう側は永久に観測不可能なのに、そこに星雲があるなどと予測することに科学的な意味があるのか?
しかし図を見れば、我々から地平線の向こうの星雲は見えませんが、その星雲と我々との中間の星雲からは見えます。地平線の向こうの星雲は、決して絵空事ではなく、中間の星雲の住人にとっては観測可能な事実なのです。まさに事実は観測者により異なるという相対性理論の原則です。
しかし、我々には中間の星雲の住人が、問題の星雲を観測したという事実を知ることはできないはずです、たぶん(ちょっと正確な考察ではないので自信なし)。我々は「中間の星雲の住人の見る宇宙も我々の見る宇宙と同様に、等方一様な宇宙だろう」という仮説の下に、「中間の星雲の住人には我々にとっての地平線の向こうが見えているに違いない」と推定しているのです。でもひょっとしたら、中間の星雲の住人は非東方的な宇宙を見ているのかも知れません。その先は滝となって流れ落ちていた、とか!!
私の結論としては、そこまで極端なことはひとまず心配せずに、見えない領域については見える領域の観測事実からの外挿で満足しておこう、というのが現代の科学の対処方法だということです。だってそれ以外には推測することさえできませんからね。決して厳密な意味での実証とか検証とかいうことはできないけれど、外挿による推測をすることには十分に意味があると考えます。「そんなわかりもしないことを考えても無駄だ」という考えもありそうで、それはそれでひとつの価値観、人生観だということは認めますが、見えない世界を推測するというのは私にとっては楽しいことですので。
本ブログの外挿の世界(2011-12-07)も参考にしてください。
---------引用開始------------
実のところ「地平線の内側で得た情報をその外側に外挿」しても良いか否かも反証は不可能です。にもかかわらず、こういう外挿についてはエリスは妥当だと考えますし、私も妥当だろうなと考えます。なぜでしょう?
---------引用終り------------
【注意】
図を見ると地平線の内側の中心角は時間が経っても変わらないように見えますが、そうではない可能性が強そうです。ちゃんと計算すればわかると思うのですが自信がないので推測だけになりますが、時間と共に中心角は小さくなるのではないかと思います。つまり、各星雲は遠い者から次々と地平線の向こうに消えていくというイメージになるのではないでしょうか?
次回はブラッホール編の予定です。
--------参考文献---------------
Ref-1) 佐藤勝彦『相対性理論 (岩波基礎物理シリーズ (9))』岩波書店 (1996/12/18)
今度は膨張宇宙の地平線の話です。これについては一般相対性理論の教科書、例えば[Ref-1])などに書かれていますが、前回も紹介したEMANの相対性理論の「ロバートソン・ウォーカー計量」から「膨張宇宙では粒子は減速する」などにも書かれています。
まずはビッグバンの前、宇宙が小さかった時から出発しましょう。ここで宇宙は正の曲率で曲がっていた、つまり4次元球面であったとします。その方が次の点で考えやすいからです。
・平坦だったとすると無限でなければ境界があることになりややこしい。
・極めて高密度だから重力で歪んでいたはずで、平坦だったとは考えにくい。
4次元球面というのはイメージすることが難しいので、普通の3次元球面、例えば膨張する風船の表面でイメージすることにしましょう。ビッグバンが始まった時、もっと言えばインフレーションが起きた時、宇宙の中の各点は相互に急激な加速度運動を行い、ひとつの点から見るとある距離以上の点は地平線の向こうへと消えたのです。まあ最初の時点は置いといて、一定の速度で膨張しているというモデルで考えます。これを4次元球の2次元断面として示すと図のようになります。

この図で4次元球面である宇宙全体に張られた座標は共動座標系と呼ばれます。星雲の運動と同時に動く座標系という意味です。それに対して各星雲や我等が銀河系に固定された慣性系は4次元球面に接する平坦な接3次元空間になります。この慣性系は星雲近傍の空間だけを近似的に表せるだけであり、宇宙全体を表すことはできません。ゆえに局所慣性系と呼ばれます。逆に言うと宇宙全体は慣性系ではありません。すると宇宙全体には特殊相対性理論は成り立たなくてもよくて光速を越えてはいけないという限界もなくなります。具体的には、ある距離以上の星雲は銀河から光速以上で遠ざかっていてもいい、ということになり、それらの星雲からの光は永久に我等が銀河系には届きません。
さてそうすると、「原理的に観測不可能、つまり実地検証のできない事について述べることは科学的に意味のあることなのか?」という疑問が生まれるかも知れません。宇宙の地平線の向こう側は永久に観測不可能なのに、そこに星雲があるなどと予測することに科学的な意味があるのか?
しかし図を見れば、我々から地平線の向こうの星雲は見えませんが、その星雲と我々との中間の星雲からは見えます。地平線の向こうの星雲は、決して絵空事ではなく、中間の星雲の住人にとっては観測可能な事実なのです。まさに事実は観測者により異なるという相対性理論の原則です。
しかし、我々には中間の星雲の住人が、問題の星雲を観測したという事実を知ることはできないはずです、たぶん(ちょっと正確な考察ではないので自信なし)。我々は「中間の星雲の住人の見る宇宙も我々の見る宇宙と同様に、等方一様な宇宙だろう」という仮説の下に、「中間の星雲の住人には我々にとっての地平線の向こうが見えているに違いない」と推定しているのです。でもひょっとしたら、中間の星雲の住人は非東方的な宇宙を見ているのかも知れません。その先は滝となって流れ落ちていた、とか!!
私の結論としては、そこまで極端なことはひとまず心配せずに、見えない領域については見える領域の観測事実からの外挿で満足しておこう、というのが現代の科学の対処方法だということです。だってそれ以外には推測することさえできませんからね。決して厳密な意味での実証とか検証とかいうことはできないけれど、外挿による推測をすることには十分に意味があると考えます。「そんなわかりもしないことを考えても無駄だ」という考えもありそうで、それはそれでひとつの価値観、人生観だということは認めますが、見えない世界を推測するというのは私にとっては楽しいことですので。
本ブログの外挿の世界(2011-12-07)も参考にしてください。
---------引用開始------------
実のところ「地平線の内側で得た情報をその外側に外挿」しても良いか否かも反証は不可能です。にもかかわらず、こういう外挿についてはエリスは妥当だと考えますし、私も妥当だろうなと考えます。なぜでしょう?
---------引用終り------------
【注意】
図を見ると地平線の内側の中心角は時間が経っても変わらないように見えますが、そうではない可能性が強そうです。ちゃんと計算すればわかると思うのですが自信がないので推測だけになりますが、時間と共に中心角は小さくなるのではないかと思います。つまり、各星雲は遠い者から次々と地平線の向こうに消えていくというイメージになるのではないでしょうか?
次回はブラッホール編の予定です。
--------参考文献---------------
Ref-1) 佐藤勝彦『相対性理論 (岩波基礎物理シリーズ (9))』岩波書店 (1996/12/18)


























Quoraで4次元宇宙論を展開しています。