タクシー数(その2)

　1729は2通りの立方数の和であらわされる最小の自然数であるが、これを拡張してn通りの立方数の和であらわされる最小の自然数をn番目のタクシー数といい、Ta(n) とあらわすらしい。つまりTa(2)＝1729である。

　以前のブログで、2通りの立方数の和であらわさせる数を生成する2変数多項式を示したが、同様のことを3通りでできないか考えてみた。そこで、まず、ラマヌジャンの師？であるハーディによるTa(n) の存在証明を振り返ることにした。なかなか見事な証明であった。

――――Ta(n)の存在の証明の概略ーーーー

　

とおけば

　

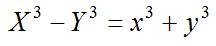
である。

　また、

　

とおけば

　

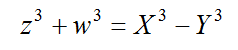
したがって、

　

とおけば

　

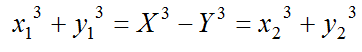
である。

ここで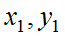を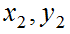に置き換え、同様の操作を続ければ

　

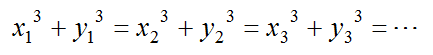
となる。ここでうまく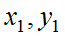をとれば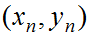をすべて異なる有理数の組とすることができる。

これらの数の分母を最小公倍数で掛ければ、n通りの立方数の和であらわされる数が存在することがわかる。

ーーーーーーTa(n) の存在証明の概略(終わり）－－－

この方法で具体的に、３通りの立方数であらわされる数を求めてみようと試みた。

 

とおくと、

 

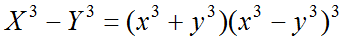
また、

 

とおくと

 

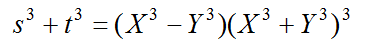
この時、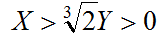　であれば、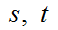　ともに正数である。

 

今、Mを2通りの立方数の和であらわされる数とする。つまり、

 

 

である。

 

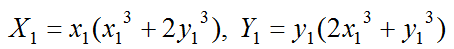
とおくと

 

これをNとおく。

また、

 

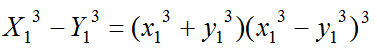
であるので

 

とおくと

 

つまり、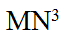　は

 

となり、3通りの立方数の和として表わされることになる(もちろん、これらの数が相異なることを示す必要はある）。

 

　以前のブログ「タクシー数」で記したように2通りの立方数で表わせる数を2つの自然数でパラメトライズできるので、3通りの立方数の和もパラメトライズすることができそうである。しかし、あまり簡単な形に表せそうもないので、ここに記すのはやめる。

　一番簡単なTa(2) の場合、つまり1729をもちいて上の計算を行ってみる。

 

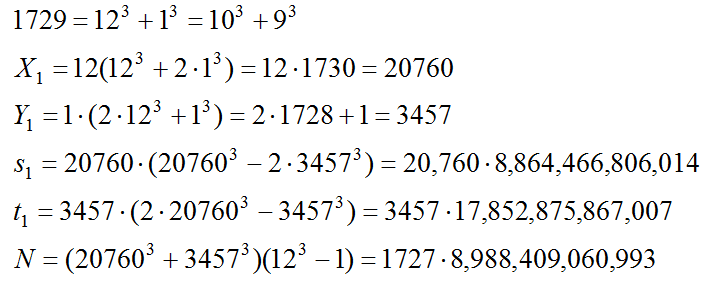
これから3通りの立方数を計算すると

 

 

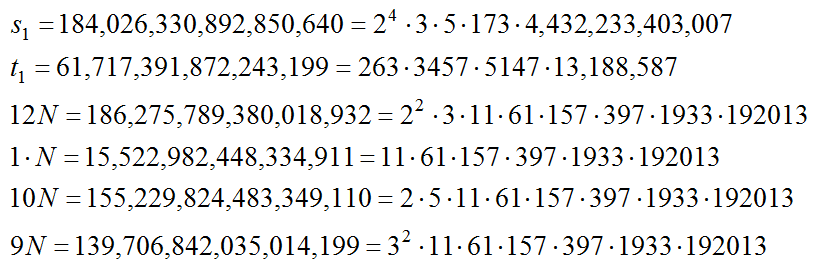
より

 

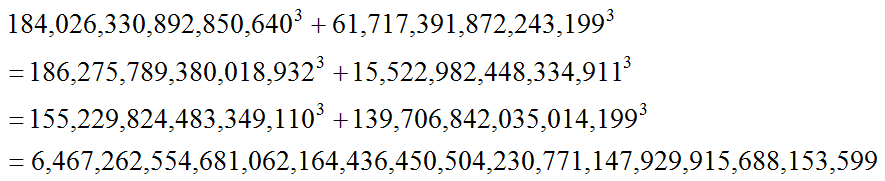
であり、上の素因数分解の結果よりこれらが共通因子を有さないことがわかる。

一方、であるので、上に述べた方法で3通りの立方数の和としてあらわされる数を求めると巨大な数になりすぎる。これはあまり良い方法とは言えないようである。

 

 

 

The Map of My Life を読む

　The Map of My Life は、数学者志村五郎氏の自伝として著名。同氏の「記憶の切繪図」の英語版と聞いていたので、英語を読むのも面倒だし、日本語の方を読もうと思っていた。が、たまたま英語版を入手できたので、試しに読んでみた。これが思いのほかおもしろい。英語は、ところどころ難しい単語がでてくるものの日本人にはわかりやすい名文である。帰りの通勤電車で読んでいたが、毎日の帰りの時間が楽しかった。
　全体的なストーリーとは関係なく、私が気になった点をいくつか書いておこう。

 

・タイトル
　まずタイトル。Mapとは抽象的な意味かと思っていた。もちろん、自分の人生を地図に見立てたとの意味ではあると思うが、冒頭に江戸切絵図の話が出てくる。氏の先祖は武士であり、その名前が牛込付近の絵図に表示されているところから話が始まる。

 

 

 

　上の地図で赤丸で囲んだ部分がそれである。切絵図大久保の図葉である。この江戸切絵図は、以下のgoo地図サイトで見られる。
　　http://map.goo.ne.jp/history/edo/map/25/
　なお、江戸切絵図は、国会図書館デジタルコレクションでもいられるが、gooの方がよりきれいである。

 

・グロタンディーク
　A.グロタンディークは2年前に亡くなった20世紀最高の数学者の一人である。
　志村氏は、ちくま学芸文庫より数学啓蒙書？四部作「数学をいかに使うか」、「数学の好きな人のために」、「数学で何が重要か」、「数学をいかに教えるか」を出しているが、グロタンディークに関する記述はほとんどない。「数学で何が重要か」の「私が会った外国人数学者たち」の項の140ページに名前だけ出てくるのと、「数学をいかに教えるか」の33ページに、半分冗談めいて名前だけ書いている2か所のみである。
　本書では、グロタンディークの話が120ページに出てくる。志村氏と小泉氏の共著論文に反例があるとの手紙が来たというのである。ある条件を記述し忘れたという話で解決したとのことで、自分の論文をきちんと読んでいる数少ない一人だと感心している。一方、グロタンディークが数学界を去ってからの活動は子供じみている、ばかげていると辛らつである。

 

・セール
 J.P.セールは、代数幾何学、整数論その他で著名な大数学者である。131ページにセールとのやりとりの話が出てくるが、セールにはどうもよい印象を持っていないようである。人生の多くの時間、イライラし不機嫌だったという意見を持つに至ったとは手厳しい。

 

・ヴェイユの娘さんの抗議
　A.ヴェイユは、志村氏がパリそしてプリンストンへと羽ばたいていく機会を提供し、同地での多くの議論を通じて志村氏の数学を高めてくれた大数学者である。
　Appendix 5にヴェイユとの思い出が18ページにわたって綴られている。米国の数学雑誌に掲載された記事である。最後の方に90歳のヴェイユとの昼食の場面が描かれている。結局これが、志村氏がヴェイユと生前に合う最後の機会となったのであるが、ヴェイユの長女から、衰えた父親についての記述の部分を削除するか短縮してほしい、との要請があったが断ったとの話が出てくる。事実は事実として正確に記述するという志村氏の姿勢は見事である。一方、こんな人がそばにいたら疲れるかもしれないとも思う。

 

 

タクシー数

現在公開されているインドの数学者ラマヌジャンに関する映画にタクシー数のエピソードが出てくる。 これは、1729というタクシーのナンバープレートが、 　

と、2通りの自然数の3乗の和であらわさられる自然数のうち最小であることをラマヌジャンが見抜いたことに由来する。

2通りの自然数の3乗の和であらわされる数が無限にあるかどうか調べてみた。

恒等式

                            

が成り立つ。この右辺が,の対称式であることに注意すれば

　　　　　　　　　　

である。,を以上の相違なる整数とすれば、上式が相異なる立法数の和を示すことがわかる。

,として小さな値を与えた例を以下に示す。

なお、100,000以下の自然数が2通りの立法数の和として表せるのは以下の場合である。