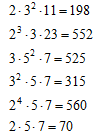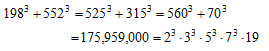タクシー数(その7)
タクシー数(その6) の続きです。前回の結論は、2通りに2次体整数の6乗数の和としてあらわされる数を求めるには、

とおくとき、①から③が成り立てば十分であった(ただし、これは必要条件ではない)。
①  が等しくなる整数の組(s,t)を求める。
が等しくなる整数の組(s,t)を求める。
今、tがsの2次式(sの2次の項の係数は1)であらわされると想定する。

に対しては、 とおくとき、t(26)=121, t(38)=1 となるb,cを求めると
とおくとき、t(26)=121, t(38)=1 となるb,cを求めると
 となる。つまり、
となる。つまり、 である。
である。
そこで、tをさらに限定して (ここでkは整数)で表わせるとして
(ここでkは整数)で表わせるとして  なる組を求める。
なる組を求める。

であるので、 を整理すると
を整理すると

左辺をs-s’で割り、sの2次式として整理すると

この2次方程式が整数解を持たなければならないので判別式が自然数(D)の平方となる。つまり
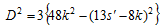 よって
よって とおくと
とおくと

さらに  とおくと
とおくと
 である。そこで、こうなる整数の組
である。そこで、こうなる整数の組 で
で が13で割り切れるものを求めと、
が13で割り切れるものを求めと、

かつ
 が13で割り切れ、かつ 偶奇が一致する (*)
が13で割り切れ、かつ 偶奇が一致する (*)
整数の組(m,n)となる (最後の条件はkが整数であることから)。
(*)は、m≡5nまたは7n (mod13) かつ m≡n(mod2)となる。
これは、m≡5nまたは7n (mod26) と同値である。
したがって、m=5n+26l または 7n+26l である。
これら2つのケースに分けて、m、k, s', s,tを求めると以下のとおり。

② 2次方程式を解いて、(s,t) から (x,y) を求める。
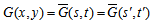 なるx,yは、
なるx,yは、 及び
及び の解として求められる。すなわち
の解として求められる。すなわち
 は
は 及び
及び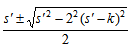
③ x,yが2次体整数の平方であらわされるかどうか確かめる。
一般に、整数ではない2次体の整数wについて、 となるためには
となるためには
 となることが必要十分。これを上記x,yに適用すると
となることが必要十分。これを上記x,yに適用すると
 が平方数でなければ
が平方数でなければ

となるU,Vが存在することが必要十分。
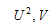 は2次方程式
は2次方程式 の解であるので
の解であるので

これをm≡5n(mod26) と m≡7n(mod26)の場合に分けてn,lで表示すると次表のとおりである。

次にUが自然数になる条件を求める。
 のとき
のとき
A. が自然数の平方になる場合を求める。
が自然数の平方になる場合を求める。
 として、
として、 の有理数解x,yを求めればよい。変形すると
の有理数解x,yを求めればよい。変形すると
 さらに変形すると
さらに変形すると
 とおくと、これは
とおくと、これは の整数解を求めることに帰着する。
の整数解を求めることに帰着する。
この整数解(の一部)は、M,Nを整数として符号を除き、 となるので
となるので
 よって、
よって、
 または
または
 を得る。
を得る。
 とおくと
とおくと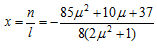 または
または である。
である。
ここで、 または
または が自然数の平方となる場合を求める。
が自然数の平方となる場合を求める。
今、 が自然数の平方とすると、
が自然数の平方とすると、
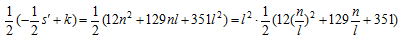 より
より
 が有理数の平方となる場合を求めればよい。
が有理数の平方となる場合を求めればよい。
 の場合を考えると、これは
の場合を考えると、これは
 が有理数の平方、つまり楕円曲線
が有理数の平方、つまり楕円曲線

の有理点の を求めることに帰着する。このペアを整数とし絶対値が小さい場合を調べると、
を求めることに帰着する。このペアを整数とし絶対値が小さい場合を調べると、
 はこの楕円曲線上の有理点(整数点)である。
はこの楕円曲線上の有理点(整数点)である。
 のとき、
のとき、 したがって、
したがって、 としてよい。
としてよい。
この時、

よって、
また、
よって、
以上より、 を得る。
を得る。
また、 のとき、
のとき、 したがって、
したがって、 としてよい。上と同様の計算で、
としてよい。上と同様の計算で、 を得る。
を得る。
上記楕円曲線が、上の2点以外の有理点を持てば、それに応じて、6乗数の和(片方は√がつく)で2通りに表される数が得られる。
長くなったので、 が平方となる場合や
が平方となる場合や
B.  が自然数の平方になる場合は、別の機会とする。
が自然数の平方になる場合は、別の機会とする。
結局、

という3乗数の和で二通り表わされるもののうち、3乗数が6乗数でもあるペアを求めていたことになる。











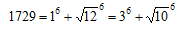


 ……………… (1)
……………… (1)  ……………… (2)
……………… (2) 
 とおくと
とおくと
 のときx,yは、
のときx,yは、 の解である。これを解くと
の解である。これを解くと
 のときx,yは、
のときx,yは、 の解である。これを解くと
の解である。これを解くと


 の形の数の計算を行ってみる。最初は簡単な
の形の数の計算を行ってみる。最初は簡単な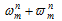 について、nの偶奇に応じて計算を行う。
について、nの偶奇に応じて計算を行う。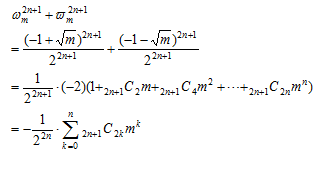
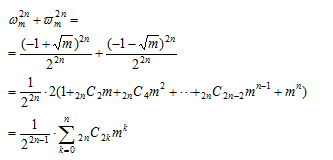

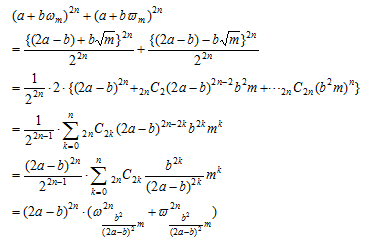
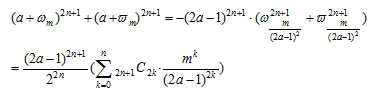
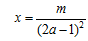 とおき、これをa,x,mの関数F(a,x,n)と考えると
とおき、これをa,x,mの関数F(a,x,n)と考えると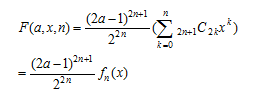
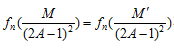 なる整数A,M,M’が存在すれば
なる整数A,M,M’が存在すれば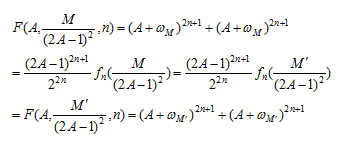
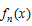 を求めると
を求めると
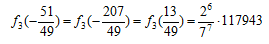
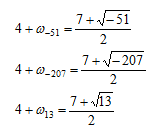
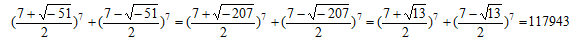
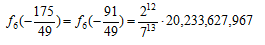
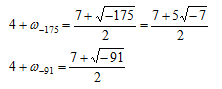
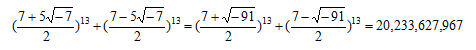
 とすれば
とすれば  はm≡1(mod4)のとき整数となるのでこの形で検討を進める。
はm≡1(mod4)のとき整数となるのでこの形で検討を進める。

 であるので
であるので

 なので
なので

 なので
なので



 であれば、
であれば、 ともに正数である。
ともに正数である。 ただし、
ただし、
 (ただし
(ただし
 なので
なので
 でこれらを割ると
でこれらを割ると