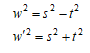 を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。
なぜなら、両辺を掛け合わせると、  したがって、
したがって、 これが成立するのは
これが成立するのは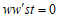 の場合に限る。
の場合に限る。 とすると、
とすると、 である。
である。 とすると
とすると となり、
となり、 である。
である。 とすると、
とすると、 となる。
となる。 とすると
とすると となり、
となり、 。したがって、必ず
。したがって、必ず となる。
となる。
同様に 非平方有理数 について
について
 を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。
なぜなら、2式の両辺に をかけると
をかけると
 よって、
よって、 より、上に述べたことより
より、上に述べたことより となる。その時、元の式に戻ると
となる。その時、元の式に戻ると である。
である。 は非平方有理数であるので、これが成り立つのは
は非平方有理数であるので、これが成り立つのは のときに限る。
のときに限る。
異なる非平方有理数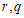 については、
については、
 は
は  と非自明の例がある。
と非自明の例がある。









