 q≠0,1の非負整数
q≠0,1の非負整数
の位数∞の整数解について考える。結果を先に記すと以下のとおりである。
(命題) 楕円曲線E: q≠0,1の非負整数 の位数∞の整数解はqが以下のときに限り存在する。
q≠0,1の非負整数 の位数∞の整数解はqが以下のときに限り存在する。
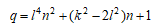 l,k: 自然数、n:0でない整数
l,k: 自然数、n:0でない整数
このとき、 は位数∞の整数解。また、
は位数∞の整数解。また、 は位数2の整数解であり、
は位数2の整数解であり、

(説明)
(x,y)が楕円曲線Eの整数点とする。 (lは自然数、nの素因数の指数は1) と平方数と非平方の積に分けると、
(lは自然数、nの素因数の指数は1) と平方数と非平方の積に分けると、
 は
は 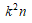 (kは自然数)
(kは自然数)
でなければならない。したがって、

より

となる。nを-nとすれば求める式となる。この時

よって、

は、Eの整数点となる(位数∞であることは示す必要がある)。
次に PとQ= (1,0)を結ぶ直線の方程式は
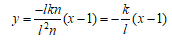
であり、この直線とEの交点のうちP,Q以外の点は 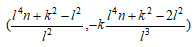 である。
である。
したがって、P+Qはこの座標のy座標の符号を逆転させた点である。 (説明終)
この命題より、Pが整数点のとき P+Q も整数点になるのはkがlの倍数になっている時に限る。
また、Pの整数倍は整数点にはなりそうもない。よって、異なる(l,k,n)に対しqの値が同じになれば楕円曲線Eのランクが2以上になる可能性が高い。
簡単のために以下l=1とする。この時、
である。k,nの値が小さい場合のqの値を計算してみると下表のとおりである。
|
k
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
9
|
19
|
33
|
51
|
73
|
99
|
129
|
163
|
|
3
|
7
|
16
|
31
|
52
|
79
|
112
|
151
|
196
|
247
|
|
4
|
13
|
25
|
45
|
73
|
109
|
153
|
205
|
265
|
333
|
|
5
|
21
|
36
|
61
|
96
|
141
|
196
|
261
|
336
|
421
|
|
6
|
31
|
49
|
79
|
121
|
175
|
241
|
319
|
409
|
511
|
|
7
|
43
|
64
|
99
|
148
|
211
|
288
|
379
|
484
|
603
|
|
8
|
57
|
81
|
121
|
177
|
249
|
337
|
441
|
561
|
697
|
|
9
|
73
|
100
|
145
|
208
|
289
|
388
|
505
|
640
|
793
|
(赤字は、素数)
この表より、素数ではq=73,31,79 について異なる(l,k,n)の組よりその値が得られる。そこで、上の命題より整数点を求めてみると、
● q=73:
(l,k,n) = (1,6,2) のとき P1=(-1,12) が整数点。 P1+Q=(37,216)
= (1,1,9) のとき P2=(-8, 9) が整数点。 P2+Q=(9,8)
であり、P1+P2=(499/49, -5760/343), P1-P2=(19,-72) となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
● q=31:
(l,k,n) = (1,3,3) のとき P1=(-2,9)が整数点。 P1+Q=(11,30)
= (1,1,6) のとき P2=(-5,6)が整数点。 P2+Q=(6,5)
であり、P1+P2=(9,-20), P1-P2=(33,-184)となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
● q=79:
(l,k,n) = (1,5,3) のとき P1=(-2,15)が整数点。 P1+Q=(27,130)
= (1,3,6) のとき P1=(-5,18)が整数点。 P2+Q=(14,39)
であり、P1+P2=(9,4),P1-P2=(129,-1456)となる。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは2である。
なお、83 以外のq<100の素数で楕円曲線Eの有理点群のrankが2となるのはこの3つのみである。83については、Cocalcで計算結果が出なかった。
● q=421:
(l,k,n)=(1,1,21), (1,5,12), (1,9,5), (2,7,4), (3,11,-3) が条件を満たす。
ここで  が解ならば
が解ならば  も解、
も解、  が解ならば
が解ならば  も解、なのでそのような解は除いた。他にも解があるかもしれない。
も解、なのでそのような解は除いた。他にも解があるかもしれない。
CoCalcで計算すると、この場合の楕円曲線の有理点群のrankは3である。
qをうまく定め、多くの整数点を有するようにすれば、対応する楕円曲線Eのrankは大きくなる可能性があると思われる。










 q≠0,1の非負整数
q≠0,1の非負整数 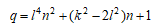 l,k: 自然数、n:0でない整数
l,k: 自然数、n:0でない整数 は位数∞の整数解。また、
は位数∞の整数解。また、 は位数2の整数解であり、
は位数2の整数解であり、
 (lは自然数、nの素因数の指数は1) と平方数と非平方の積に分けると、
(lは自然数、nの素因数の指数は1) と平方数と非平方の積に分けると、  は
は 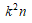 (kは自然数)
(kは自然数)



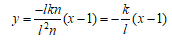
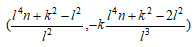 である。
である。 が解ならば
が解ならば  も解、
も解、  が解ならば
が解ならば  も解、なのでそのような解は除いた。他にも解があるかもしれない。
も解、なのでそのような解は除いた。他にも解があるかもしれない。