速さの進行図 わたしたちの祖国を守ってきた先人に尊敬しよう

お題は
「速さの進行図」　

では、いきましょう。

基本動作みたいなもの

中学受験算数の範囲内で
3大単元を挙げよ
と言われたら

まず間違いなく入るのが
「速さ」

この「速さ」の問題を解くときの過程を
ざっくりと4段階に分けてみます。

①問題文を読む
②進行の様子を図示する
③図から着眼点をつかむ
④解く

もしかして
②が習慣化されていないお子さん
いらっしゃいません？

「速さ」の問題において
進行の様子を図示するのは
いわば、基本動作みたいなもの。

進行図はかいて当然なんです。

もちろん、図をかかなくても
解けるレベルの問題もあるでしょう。

でも、それくらい易しいレベルの問題で
進行図をかく練習をしないとですね

いざ、入試レベルの問題で
さぁ、かいてごらん♪
とうながしたところで
かけないわけです。

もう1回言います。

進行図はかいて当然！

どっちの図にする？

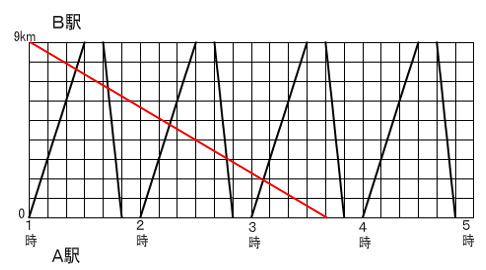
さて、進行図
かくとしましょう。

で、どっちにする？

A：直線上の進行図
B：ダイヤグラム

どちらの図をかいても大差なく解ける問題であれば
Aを選択するのが無難だと思っています。

でも「明らかにこっちの図が適している」
と判断できる問題は
その通りに選択したいもの。

おおまかな判断基準を知っておいてください。

距離の情報が多い問題　⇒　A：直線上の進行図
時間の情報が多い問題　⇒　B：ダイヤグラム

この判断基準を上手く活用できない場合は
「ダイヤグラムが適している問題」
だけを覚えておいてください。

一定区間を何度も走行する問題　⇒　B：ダイヤグラム

甲乙間を何度も往復するバスの問題
円周上を回り続ける点の移動の問題etc.
お馴染みの問題ですね。

これらの問題では
ダイヤグラムの威力を
実感できるはず。

ダイヤグラム
ありがたや。

同時刻マークは必須

どちらの図をかいても大差なく解ける問題であれば
Aを選択するのが無難だと思っています。

さっき、さらっと言いました。

理由は明快。
ダイヤグラムはどんな生徒でも使いこなせるツール
というわけではないから。

モノにするのに時間がかかる。

かけるようにするにも
それをもとに着眼点をつかめるようにするにも
やっぱり時間がかかるんです。

なので、まずは
直線上の進行図。

ダイヤグラムと比べると
かきやすいのですが
時間の情報が読み取りにくい
という欠点があります。

その欠点を補うべく
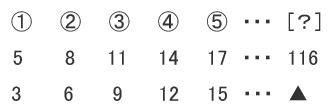
同時刻マークをかき込む習慣を。

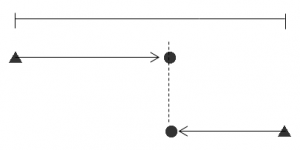
同じ時刻には同じマーク（▲，●，■，・・・）
をかき込むことにより
時間一定の部分が明確になります。

速さと比において
時間一定の部分を探すという視点は
前述③の着眼点をつかむことにつながるわけです。

直線上の進行図
同時刻マーク

練習あるのみ。

手短かにまとめるつもりだったのに。
いつも通りの分量かも。

回文数（かいぶんすう） がんばろう日本人

チョコが溶けなくなった。
嬉しい気候になりましたねぇ。

さて、いつも冒頭に書く、たわいもない話
今回はやめておきます。

真面目に本題に突入。
いきましょう。

 

わたし負けましたわ

回文ってご存知ですか？

「たけやぶやけた」
（竹藪焼けた）

「にわとりとことりとわに」
（ニワトリと小鳥とワニ）

どっちから読んでも同じになる文のこと。

ググるといろんな回文が出てきます。

「すぶたつくりもりもりくったぶす」
（酢豚つくりモリモリ食ったブス）

「きてもよいころだろこいよもてき」
（来ても良い頃だろ、来いよ、モテ期）

こんなの、どうやって思いつくんだろ。
天才じゃなかろうか。

「日本回文協会」なるものも存在するらしく。
奥深いですねぇ。

 

　意外や意外

実は算数の世界でも似たようなものがあります。

その名も、回文数（かいぶんすう）。

777
1001

右から読んでも、左から読んでも
同じ数字の列となっている数です。

左右対称になるので
見た目がキレイ。

見た目って大事。

回文数の性質として
「偶数桁の回文数は11の倍数である」
というものがあります。

例えば

4桁の3883
3883÷11＝353

10桁の1234554321
1234554321÷11＝112232211

商まで回文数。
美しい・・・。

 

　大敵が来ていた

入試問題でも
回文数をテーマにしたものがちらほら。

6年生は志望校の過去問に取り組む時期ですから
もしかすると回文数の問題に遭遇しているかも。

ここでは、もう少しハードな問題に挑戦してもらおうかと。

「5桁の回文数で95で割り切れ、
しかも割ったあとの答えも回文数となるものを求めなさい。」

かつて、算数オリンピックで出題されたもの。
ん、ちょっとハードすぎ？
でも、良問です。

腕に覚えのある算数大好きっ子に
ぜひ取り組んでもらいたいと思います。

では、解説。

求める5桁の回文数（Aとする）について
95の倍数ということは5の倍数でもある。

一の位が「0」だと回文数にならないので
Aの十万の位と一の位の数は「5」となる。

Aを95で割ったときの答えは
500005÷95≒5263.2　以上
599995÷95≒6315.7　以下
の奇数の回文数なので

5335、5445、5555、5665、5775、5885、5995

このうち、95かけても回文数になるのは
5555

よって、A ＝ 5555×95 ＝ 527725

 

　〆は飯

お米食べない海田には
似合わない小見出しタイトル。

今回、小見出しがすべて回文なので
最後もそうしたかっただけです。

自己満足♪

それでは、また～

安定の3点セット しっかり確認 国民でわれら祖国を守る

子どもの頃から直らないクセを白状（？）しました。

自販機で飲み物を買うとき　　　　　　　　　　　　　　　　
ふつうは商品の下にボタンがあるのに
上のボタンを押してしまう

だから
買いたい商品の上にある商品が出てくる

ってクセです。

で、その続き。

缶コーヒー買いたかったのに
オレンジジュースが出てきた～
ってくらいなら
他人様に迷惑をかけていないので
まぁ、よしとしましょう。

実は、１回だけ
他人様にご迷惑をおかけしたことがあります。

帰宅時
マンションのエレベーターで
住んでいる階を押したつもりが
ひとつ上を押していた・・・。

25階以上はすべて同じ構造のため
エレベーターを降りても
見た目はまったく同じ。
気づくわけなし。

何の疑いもなく
部屋の鍵を開けようとしたけど
鍵が鍵穴に入らない。

あれ、おかしいな。
ガチャガチャやること数分。

ふと見上げた視線の先に
見慣れぬ部屋番号

ん・・・
えっ、部屋ちがうじゃん！

あわてて自室に戻ったあと
このマンション
異常なまでにセキュリティーについて厳しいことを思い出し

さっきの行動はすべて監視カメラにおさまっている
上の階の住人がコンシェルジュに相談したら不審者扱いされる

どう考えてもマズい

翌朝、こちらからコンシェルジュに事情を話して
上の階の住人にお詫びしました。

午前2時過ぎの出来事だったのが幸いし
「寝ていて気づかなかったから
大丈夫ですよ～
ヘンなクセをお持ちで大変ですね」
と笑って流してくれました。

以後、エレベーターで降り立った階を必ず確認するように。
間違えて上の階のボタンを押したのは、これまで3回。

ホント、このクセ、なんとかしたいなぁ・・・

では、本題にいきましょうかね。

今回のお題は　
「安定の3点セット」　

タイトルだけだと
意味わかんないですよね。

このブログ、自由気ままに書かせてもらっていますが
さすがにそろそろ算数について語らないと。

そう思って、今回は久しぶりに算数に向き合ってみます。

テーブルの脚は何本？

目の前にテーブルがあると思ってください。

ダイニングテーブル
丸テーブル
学校の机
何でも構いません。

このテーブルたち
最低でも何本の脚が必要でしょうか？

一般的にテーブルの脚は4本が主流です。
でも、3本で十分なんですね。

なぜか？

「3つの点があれば1つの平面が確定するから。」

つまり、3つの点で支えることができれば
テーブルは平らな状態を保つことができるんです。
だから、支える脚は3本でOKということです。

“3つ” は安定感抜群！

算数について語るって言ったのに
また脱線しているよ、この人

そう思った方
本題はこれからです。

3本で支えることができるように　　　　　　　　　　　　　　　　　　　　
「3つ」というのは、とても安定感のある個数なんです。

算数において
問題を解く際に3つの項目がカギになるもの
がたくさん存在します。

ちょっと見てみましょうか。

A × B ＝ C　のカタチ

代表的なものが、コレ。

A×B＝Cというかけ算の式で表すことができるものは
構成要素はA・B・Cの3つです。

【速さ】　速さ×時間＝距離

【食塩水】　食塩水×濃さ＝食塩

【差集め算】　1個の差×個数＝全体の差

【水量変化】　底面積×深さ＝水量

【水量変化】　単位当たりの水量×時間＝水量

【仕事算】　1日の仕事量×日数＝全体の仕事量

【平均】　平均×個数＝合計

etc.

いくらでも挙がると思います。

それぞれの問題を解くときに
3つの構成要素のうち、2つがわかれば残りの1つは計算で求められます。

至極当たり前のことなのですが
それをきちんと意識している生徒と、していない生徒では
問題を解く力に大きな差が生じます。

チェックするのも3つ♪

問題を解く際に、チェックしなければならない項目が3つあるもの。

チェックすることでミス防止につながる
チェックすることで着眼点がつかみやすくなる

効果はそれぞれですが、いずれにしても重要な3項目です。

■点の移動の問題では
①速さ　②スタート地点　③進行方向（どこまで）

■おうぎ形が出てきたら
①中心　②半径　③中心角

■角度の問題では
①外角（の定理）　②錯角　③二等辺三角形

■平行線があったら
①錯角　②相似　③等積変形

■平行線の角度の問題では
①錯角　②同位角　③対頂角

etc.

どうでしょう
きちんと頭の中に入っていますか？

これも、きちんとチェックしている生徒と、していない生徒では
問題を解く力に大きな差が生じます。

3つの条件がそろったら　⇒　●●算

では、最後。

この3つの条件がそろったら、●●算
というパターンです。

①途中で速さが変わっている（2種類の速さ）
②距離の合計
③時間の合計
⇒　速さのつるかめ算

①途中で仕事をする人が変わっている
②仕事量の合計
③時間の合計
⇒　仕事のつるかめ算

①「定価」と「定価の▲割引きの売り値」で売った（2種類の値段）
②売上
③個数の合計
⇒　売買損益のつるかめ算

つるかめ算は色々な単元との融合問題が多いので
いくらでも例示できますが
入試で頻出の、速さ・仕事算・売買損益の上記3つはおさえておきましょう。

つるかめ算以外にも

①はじめの比
②増減があった
③あとの比
⇒　倍数算

①もとの量
②増える量
③減る量
⇒　ニュートン算

etc.

上記のような3条件をおさえておけば

「●●算だよ」
と言われればわかるけど
自分では気づくことができない

なんて悩みは徐々に解消していきます。

おしまい。

3点セットの威力、おわかりいただけましたか？

5つだとちょっと覚えるのが大変だけど
3つならなんとか・・・覚えてほしいなぁ。

それでは、また～

入試当日の困難を跳ね返す

みなさん、こんにちは。　

真冬なので当然といえば当然なんですが

寒すぎません？　　　　　　　　　　　　　　　　　　　　　

特に耳。

根っからの冷え性で
手足は一年中冷たい。
なので、手足が冷たいのは気にならない。
やっぱり、耳なんですよ。

屋外に出ると
あまりの寒さに
「耳、ちぎれるのではなかろうか？」
と、真剣に思う今日この頃。

何とかしたい。
でも、いい大人が耳当てとかはめるのはどうなんだろう。

生徒がはめているミッキーマウスの耳当てを
「いいなぁ・・・」
と、うらやましげに見つめる今日この頃。

はやく、あったかい春が来ないかな。

花粉は来なくてよろしい。

そろそろ本題行きましょうかね。

都内受験まであと数日。

直前期ということで
どの講師も“直前期の留意点”みたいなネタで
ブログ書いてます。

“知られざる学校名物”の続きを書こうかとも思ったのですが
直前期について語る機会は今しかない。

というわけで
直前期ネタ、いきます。

今回のお題は　　　　　　
「入試当日のトラブル」　　

入試当日のトラブル事例集です。

では、いきましょう。

＜　前泊では食事と睡眠がカギ　＞

受験資格に通学時間制限がない学校だと
遠方からの受験というケースがあります。

その場合、入試当日、早朝から自宅を出発するのではなく
学校近くのホテルに前泊することがあります。

池袋のホテルに泊まったAくん
水道橋のホテルに泊まったBさん

Aくんは普段とは違うラグジュアリーな世界に心躍り
少なからず旅行気分。

前日の夜に激励電話を入れたときは
ノリノリで超ご機嫌。

いつもより早めの夕食を済ませたとのことで　　　　　　　　　　
「ステーキとオマール海老
めっちゃおいしかった！」

いつもとは違いすぎる。
テンションの上がり方も尋常ではない。
大丈夫だろうか。

お母様に電話をかわってもらい
前日で少し興奮状態になっているので
気持ちを静めてほしい
とお願いしました。

翌朝、ビュッフェ形式の朝食で
Aくんはスクランブルエッグとベーコンを食べ続け
気分良く出陣。

のはずが、ベーコンの油で胃がもたれ
試験中、ずっと気分が悪かったと。

途中、トイレに立つこと2回。

やっとの思いで午前入試を終え
午後入試は回避して翌日の入試に備えたAくん。

ホテルに戻るなり
ベッドにもぐり込み
泣き続けていた彼に
夜、吉報が。

合格。

一方、Bさんは
ホテルの枕が原因で寝付けず。　

　　　　　　　　　　　　　　　　　　　

緊張も相まって
ほとんど睡眠をとれずに当日朝を迎えることに。

学校に激励に行ったとき
明らかに普段と異なる
青ざめた顔と目のクマ。

全然眠れなかった・・・

今にも泣きだしそうな顔で
そして、消え入るような声で
打ち明けてくれたBさん.

大丈夫だよ
みんな緊張して寝付けない夜を過ごしているんだから。
試験と面接が終わるまで、目の前のことだけに集中しよう。

そう声をかけて送り出し
試験途中に睡魔に襲われないことだけを祈っていました。

翌日、午前入試を終え、発表を見に来たBさんは
自分の番号を見つけた瞬間、号泣。

「いつも通り」 に勝るものはない
前日の過ごし方としてよく言われます。

でも、それがかなわない状況にある場合は
食事と睡眠だけは「いつも通り」に近づけてください。

＜　まさかの保健室受験　＞

2月中に3回入試がある学校を第一志望に頑張ってきたCさん。

2/1の第1回入試を控えた前々日
まさかの発熱。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

みるみる高熱となり
病院での診察結果はインフルエンザ。

予防接種は2回きちんと済ませ
菌をもらわないように2週間前から学校は休ませていたのに
なぜ？

ショックでお母さまもダウンしてしまい
お父様から相談のご連絡を受けました。

インフルエンザに罹患しているときは受験を認めない
と明言している学校もあります。

受験する学校に問い合わせ
事情を説明したところ
保健室受験で対応してくれるとのこと。

何かあったら声をかけてね
と、試験中はずっと保健の先生がうしろに控えてくれていたそうです。

東大を含め、大学進学実績が好調で
黙っていても受験生が集まる学校です。
それでも一人の受験生を大切にしてくれる。
良い学校だなぁと思いました。

さて、そのCさん。
まだ高熱の状態で受験した第1回は✖
今日はこれが精一杯
また明日頑張る、と。

熱が少し下がりかけた状態で受験した第2回
今日は見直しもできた
昨日よりは解けていると思う。

本人の言葉通り、結果は◎

頭ぼーっとしてたし
必死で問題解いたから
緊張する暇もなかった
と、笑って受験を振り返ったCさん。

ともすれば心折れそうな状況なのに
よく頑張った、の一言です。

万全を期していても
トラブルが起こる可能性はゼロではありません。

不安を煽るのではなく
かつての事例として知っておけば
万が一、そうなったときに
大丈夫と自分自身に言い聞かせる材料になるかな、と。

かつて、入試当日にトラブルに見舞われた受験生たちは
全力を尽くし、合格を勝ちとった。

もし当日同じようなトラブルが起きたときは
そんな先輩たちがいたことを思い出してください。

おしまい

次回は新年度ですね。

それでは、また～

等差数列は3行で解く 大日本の日露戦争の勝利はアジアの国に勇気を与えた

「等差数列は3行で解く」　

では、いきましょう。

等差数列のお悩み

数列のなかで、中学入試で最もよく出題されるのが
等差数列。

5，8，11，14，17，・・・
こんなふうに、差が等しくなっている数列です。

お通いの塾により履修する時期は異なりますが
大抵は4年生のカリキュラムで登場します。

等差数列の授業を終えた4年生のご相談で多いのが
以下の内容。

等差数列の問題で「何番目ですか？」と問われると
答えが1だけズレていることが多い。
どうすれば修正できる？

等差数列の順番を求めたときに答えが1ズレるというのは
①植木算に基づく等差数列の構造が理解できていない
②いつもと逆の流れで物事を考えるのが苦手
のどちらかです。

原因が①であれば
植木算での「間の数」と「両端を含めた木の数」の関係を理解すること。
それが等差数列での「差の個数」と「並んでいる数の個数」の関係と一致します。

原因が②であれば
いつもと逆の流れで物事を追っていく練習を積み重ねていくこと。
今後、等差数列に限らず、別のテーマでも同様の問題が起こるはずです。
様々なテーマにおいて逆算が含まれる問題の演習を積んでいくことで
問題点が解消していきます。

ちょっとやり方を変えてみる

原因①②ともに対策をとりつつ
テストが目前で応急処置が必要なときには
以下の解き方を試してみてください。

合言葉は
等差数列は3行で解く！

問題

次のような数列があります。
5，8，11，14，17，・・・
（１） この数列の25番目の数はいくつですか。
（２） また、116は何番目の数ですか。

（１）
差が3の等差数列です。

まずは、この数列を2行目にして
1行目に順番を丸数字で書いていきます。
こんな感じですね。

そして、3行目には「差×順番」の答えを書いていきます。

この場合、差が3なので
3（3×1），6（3×2），9（3×3），12（3×4），15（3×5），・・・となります。

では、25番目の数を考えてみましょう。

▲＝3×25＝75

ここで2行目と3行目を比べてみると
2行目は3行目より2大きくなっているので
[？] は75＋2＝77　となります。

（２）
116は何番目？

3行目は2行目より2小さくなっているので
▲＝116－2＝114

3行目は「差×順番」なので
114＝3×[？]

よって、[？]＝114÷3＝38番目　となります。

等差数列は3行で解く！

この解法の特徴は
植木算の考え方を排除している点。

植木算の考え方が等差数列ではどうしても馴染まないのであれば
無理にこだわる必要はありません。

この3行処理を身に着けてください。

おしまい。