図を描く～〇描いて みんなで大きい和 それが大和

問題を解くときに、「手をうごかして」「とにかく描く」といわれることが
多いのではないでしょうか。
しかし、どのように描くのか。問題集やテキストの解説には完成図は描かれているのですが、
実際どこから描くのか、それを示してくれていません。

そこで、本日は、描く手順を示していきます。

次の図を見てください。

この図って、「水量とグラフ」の単元を勉強するときによく見る図ですよね。

この図ってどこから描くのでしょうか。
授業をやっていても、話しながら、少しずつ問題を紐解きながら
解いていくのですが、「じゃ、描いてみて」と言ってやらせてみると、
ただ、なぞって上のほうからL字型にいきなり描いたりします。

そうではなく、
描く順番があるのです。

お絵描き歌というのを小さいころやったことがあると思います。
ドラえもんを描くときも、「♪〇描いてチョン、〇描いてチョン♪」
とリズムと歌に合わせて描いたと思います。

それです！！
まず描く順番があります。
【問題】
底面積が500㎠で、深さ20㎝の直方体の形をした水そうと、一辺10㎝の立方体のおもりがあります。
いま、水そうに6㎝まで水をいれました。
立方体のおもりを1つ入れると水の深さは何㎝になりますか。

まず、
手順①水そうを描きます。

手順②入っている水の深さ5㎝という横棒を入れます。

手順③おもりを沈めます。

手順④おもりを入れた後の水の深さを表す横線をいれます。

手順⑤上がった分₍イ₎とおもりが入る前にあった水（ア）の部分が等しいという図をいれます。

手順⑥底面積の比を求めます。

ここが解くポイントになります。『イメージde暗記　根本原理ポイント365』の基本編070、実践編163にありますのでお持ちの方はチェックしてみてください。
底面積比がア：イ＝100㎠：（500－100）＝1：4となります。
アとイの面積が等しいので、ア：イの横の比が1：4となり、たての比は4：1と逆比が成り立ちます。
そうすると、下の図ができあがります。

4⃣＝6㎝
1⃣＝1.5㎝になります。

水の深さは、6＋1.5＝7.5㎝と求めることができます。

いかがでしょうか。
自分1人で描けるかどうかやってみてください。

授業の中では、横にいて描いている過程を見せます。
それをまねして家でやってきてほしいと思っています。

この単元だけではなく、どの単元もイメージ図が大事です。
描き方を示し、まねして、練習するというサイクルを作っていきます。

ひとひねり問題～角度編～ がんばろう日本男子 わが国も大和撫子も日本男子が守る

「算数の問題が解ける」ということは、
① あることに気が付いて
② 式を計算することができて
③ 答えが出る

このスリーステップを踏んでいるのではないでしょうか。

この①の「あることに気が付いて」
という部分が、ぱっとわかる問題か、手を動かして何かを書き出して気づける問題と、
またその中間の問題があると思われます。

ぱっとわかる問題というのは、5年生の前半で終わると考えてください。
5年生の前半までで、算数の気づかなくてはいけないポイントを
教えてもらっているということになります。その気づかなくてはいけないポイント
というのは、今後の5年生後半、6年生、入試に続く重要なポイントとなります。

重要ポイントは、
『イメージde暗記　根本原理ポイント365』の基本編100、実践編265にあります。
ちょっと宣伝が入ってしまいましたが。

それでは、そのポイントをどう使って、どう解くのかを例を使って示していきます。

こちらの角度の問題はどうでしょうか。
問題：角アは何度か求めなさい。

これは練習を積んでいる皆さんは、
○○＋✖✖を求めて、〇＋✖にもっていけばいいと気づくと思います。（気づいてほしいです）
〇〇+✖✖＝180－58＝122
〇+✖＝122÷2＝61°
ア＝180－61＝119°

では、ひとひねりされているとどうでしょうか。

問題：　右の図の三角形ＡＢＣで、角Ａは66°、ＢＤ＝ＢＥ、　ＣＥ＝ＣＦ
です。このとき、角アの大きさを求めなさい。

二等辺三角形なので、底角が等しいというのは知っていますよね。
ステップ①
同じ角度には同じマークをつけましょう。

同じ辺にはチョンチョンマーク。
同じ角度には、〇や✖で同じマークをつけましょう。

そして
アを求めるためには、〇＋✖がわかればいいということまで来ました。

では？？

次に66°をどのように使うかです。
よく授業中も言うのですが、
算数の問題ででてきた数値というのは使わないということはほぼないと考えてください。
問題の中の情報はすべて使うという意識で問題を解くのもポイントの一つとなります。

66°は三角形の内角なので、
他の2つの角度の和は、180－66＝114°

あと少しです！！

ということは、
〇〇＋✖✖は2つの三角形に入っている角度なので、
180×2＝360°

360°-（イ＋ウ）＝360°－114°＝246°
○○＋✖✖＝246°
〇＋✖＝246÷2＝123°

よって、
ア＝180°－（〇＋✖）＝180°-123°＝57°
となります。

まとめると、

角度の問題で気づかなくてはいけないポイントは、
① 二等辺三角形、正三角形を探す
→角度がわかる図形があれば簡単！
② 同じ角度、同じ辺には同じマークをつける
→二等辺三角形、正三角形を探すため
③ いったん〇と✖など記号でおいてみる
→答えは出ないが、使えないかと疑う
この3つです。

そして、この問題のひとひねりは、
〇+✖が一回では求められないということです。

ぱっとみてわかる問題ではない時に
考えなくてはいけないことは、やはり気づかなくてはいけないポイントをまずは頭に
入れているかということです。ここは、本当に基本中の基本で、根本原理となります。
つまり、とっても大事なところということです。

そして、それを頭にいれながら、
どれが使えるのかなと考えながら手を動かし（ここではちょんちょんマークをつけるとか）、
自分で気づけるようにしていくということです。

スペース間隔を考えて計算しよう 愛する祖国愛する家族愛する夫婦

「計算」に的を絞ってお話しいたします。
計算ミスをなくすためには、
計算スペースをうまく取るという感覚を養うことです。

どういうことかと言いますと、
計算力は皆、高い水準を持っています。
しかしながら、テストでは数値の見間違いや繰り上がり、繰り下がりミスを起こしてしまい、
「うちの子、必ず【1】で1問落としてしまうんです」
というご相談を多く受けます。

今まで、私もあらゆる計算問題集、小学校で習う計算方法など
人に聞いたり調べたりして、計算力を上げなくてはと問題を解かせることに注力していました。
しかし、ある時ふと、実際自分の担当させていただいている生徒さんのやり方を見ていて、
あれ？？と思ったことがあったのです！！

それは、

スペースの取り方の感覚が下手な子がいるということです。

下の例で、
【資料1】では、生徒さんが実際に受けたテストの一部です。
3月の時点でまだ、式と式の間に計算した数値を小さく書き込んでいたり、
覚えるべき数値、例えば、1/8＝0.125をパッと変換することができず、125/1000を約分した跡が
残っています。しかもそれを細い行の隙間にやってしまっていますね。問題の字と
自分の字が重なってしまっています。
かなり計算力はある生徒さんでも、まだ3月の時点では覚えられていなかったのか、
不安だからやったのか、どちらかでしょう。
③の問題では、右の余白にそれぞれの式を書いて計算しているのは良いと思います。
ただ、途中で終わっている？　諦めてしまったのか、最後までの計算がありません。

【資料1】

そして、【資料2】は、同じ生徒さんで6月に行われたテストです。
少し成長が見られます！

①は、16が両方の式に共通しているので、16でまとめて、16×（18+12）＝16×30です。
途中で気が付いていますね。良かったです。
②もしっかりと右の余白に書いてますね。ただ、「30」が31なのか30なのかが見えにくいですね。
しかしながら、余白をうまくつかうということは意識しているように思います。
③も、どことどこの式がつながっているかがわかるように区切りをつけてますね。
その部分だけを計算して後でまとめるということができています。
授業の中で指導していることを、ちゃんと再現してくれた時は、間違っていても
褒めてあげます。「意識」することが大事です。常に「意識」していれば、
繰り返し、繰り返し、こちらも指摘していきますし、それが、最後ちゃんと
できるようになればいいのです。

【資料2】

学校によっては、計算スペースが本当に少ない学校もあります。
女子学院などが良い例かもしれません。ほとんど書くスペースがないので、
やはり計算力を上げるために、暗記しておくべき数値や工夫すべき計算はそのまま計算しない
など、徹底して技を磨く必要があります。

学校別の対策はありますが、
まずは、組分けテスト、公開模試で、計算スペースをうまく活用することを意識していきましょう！

左のスペースが空いているのに、なぜか右端にちょこちょこっと書いてしまう生徒さんもいます。

「なぜ右隅に書く？」
「左のスペース、いっぱいあいているよ。」

こんな会話を授業のなかで行っています。

ご家庭でもお子様のテストを確認してみてください。
もしスペースを活用できていないのであれば、
まずはスペースを有効活用することからはじめてみましょう。
次の組分けテスト、さぁ頑張ろう！

高さの等しい三角形の見つけ方 家の長のお父さんが家族の大黒柱

問題：三角形ＡＢＣを下の図のように、3本の直線で面積を4等分しました。

辺ＢＤ：辺ＤＦ：辺ＦＣを求めなさい

 

 

上のような図計を6年生であれば見たことがあると思います。

長さの比を求めなさいという問題になると、

生徒さんたちは、すぐに長さを出そうとして、

三角形の面積の公式底辺×高さ÷2に当てはめようとします。

 

しかし、この問題は一切面積や長さはでていません。

 

ではどのように求めるのか。

 

もう一度問題に戻ると、

どういう情報が与えられているか見てみます。

 

「面積を4等分した」ここがポイントです。

 

面積を4等分したので、面積比は全て１：１：１：１となります。

つまり比を使うしかないということがわかります。

面積比から底辺比を求める

ためには、

↓

高さが等しい三角形を探す

↓

高さが等しいので比べられる

↓

面積比から底辺比が求められる

 

という思考になります。

 

 

ここまでは理解しつつも、

その先に「高さの等しい三角形」を見つけることができない

という症状がでてきます。

 

本日のメインのお話はそこです。

じゃ、どうやって高さの等しい三角形をみつけるか。

 

底辺と頂点を決める

 

これが今日のポイントです。

 

三角形ＡＢＤと高さが等しい三角形はどれでしょうか。

 

まず、三角形は、３つの辺と３つの角度でできているということに

注目しましょう。

 

3つの辺のどこを底辺にしてもいいのです。

しかし、高さが等しい三角形を見つけるときは、

底辺を同じ位置に取らないといけません。

 

三角形ＡＢＤの底辺を例えば、辺ＡＢとします。

高さを決める「頂点」は、点Ｄとなり、

 

 

頂点から底辺に向かって垂直に下した線が高さ

 

しかし、これだと高さが等しい三角形は見つかりません。

 

高さが等しい三角形は、頂点の1点に集まっているものです。

つまり、

底辺を決めたら、高さが等しい三角形は、

右か左（となり）にしかないのです。

その右か左を底辺として、頂点の1点に集まっているものを見つけます。

 

底辺をＢＤにすると、

頂点は点Ａ

 

点Ａに集まっていて、底辺が右か左に

あるもの

 

を探します。

 

 

底辺をＤＣとし、頂点Ａに集まっているものは、

三角形ＡＤＣとなります。

 

辺ＢＤ：辺ＤＣ＝①：③となります。

 

更に、辺ＤＦと辺ＦＣを求めたいので、

高さが等しい三角形を同じように探すと、

 

 

三角形ＥＤＦと三角形ＥＦＣが頂点Ｅに集まっている

高さの等しい三角形となります。

 

辺ＤＦと辺ＦＣは１：１

 

よって、先ほどの

辺ＢＤ：辺ＤＣ＝①：③と

辺ＤＦと辺ＦＣは１：１

をあわせて連比すると、③＝２となるので、6にそろえて、

辺ＢＤ：辺ＤＦ：辺ＤＣ＝２：３：３となります。

 

同じように、

辺ＡＥ：辺ＥＣも求めることができます。（答えは一番下の行にあります）

 

ぜひトライしてみてください。

高さの等しい三角形は、

 

まず底辺を決めて、頂点を見つける

頂点の1点に集まっている三角形を見つける

高さの等しい三角形は右か左にしかない

 

今日のポイントは以上3点です。

 

答えは、辺ＡＥ：辺ＥＣ=1：2となります。

 

帰国子女 祖国へおかえり 自分の国がある幸せ

とある帰国子女の生徒から
「ねぇ先生、これであってる？」

差し出された国語のプリント。

次のことわざは
すべて同じ意味を表しています。
［　　　］にあてはまる言葉を書きなさい。

（１）［　　　］の川流れ
（２）［　　　］も木から落ちる
（３）［　　　］も筆の誤り

よく見聞きすることわざですね。

で、生徒の答えはというと
（１）［　もも　］の川流れ
（２）［　りんご　］も木から落ちる
（３）［　ツイッター　］も筆の誤り

なかなか個性的ですな。
なぜにこの答え？

本人曰く
（１）「だって桃太郎のことでしょ？」
・・・日本の昔話で知っているのが
桃太郎と鶴の恩返しなんだそう。

（２）「知ってるよ、ニュートンの万有引力の法則♪」
・・・いや、違うから。

（３）「お姉ちゃん、しょっちゅうツイッターに間違ったこと書き込んでる
ヤバいよね～」
・・・時代は変わったもんだ。

これさ、全部同じ意味のことわざって書いてあるよね。
どんな意味だと思ったの？

「ん・・・なんか～
起きたことは仕方がない、気にするな！　みたいな意味？」

おぉ、超ポジティブ。

この軽やかさがある限り
怖いもんなし。

さて、ここからつなげて

今回のお題は　「帰国子女の算数指導」

以前、メルマガのインタビューで
帰国子女の算数指導における留意点
みたいな内容を語った記憶があるのですが。

あれから月日もたっていることですし

頭の中で日々つらつらと考えていること
指導の現場で実際に行っていること

あらためてまとめてみようかと。

国語のタイヘンさに比べたら
算数のタイヘンさなんてたいしたこたぁない。

そう思って取り組んでいますが

でもね、講師としての葛藤は続くんですよ。

では、いきましょう。

　コトバの問題は避けて通れない！？　～　その1　

帰国子女の指導

突き詰めれば
コトバの問題です。

巷でよく言われる
問題文の読み取りについて
ハンデがある点。

確かにその通りです。

知らない表現に遭遇するのはしょっちゅう。
混乱する生徒もいれば
勝手な認識をしてとんでもない方向にいく生徒もいる。

それを目の当たりにして
ご家庭が焦るのも当然。

ただ個人的には
問題文の読み取りについて
さほど気にしていないんです。

なぜか？

コトバによる問題文の読み取りのハンデは
時期が来ればほぼ解消することがわかっているので。

一定の演習を重ねることで
算数の問題文でよく出てくる表現は
自然と取り込まれていきます。

例えば、旅人算でのおきまりの表現
「出会う」と「すれ違う」
「追いつく」と「追いこす」

コトバは違えど同じ意味。
はじめは混乱していますが
徐々に同じものと認識してくれます。

また、一定の演習を重ねることで
「よくわからないけど
算数の問題文だから
おそらくこんな意味なんだろう」
と推測する力が養われていきます。

日本語のすべてを理解させる必要はありません

あくまでも
中学受験の算数で必要なコトバを理解させる
中学受験の算数でよく出てくる問題設定を理解させる

それで十分なんです。

　コトバの問題は避けて通れない！？　～　その2　

じゃあ、コトバの問題は気にしなくていいんだね。

生徒自身は気にしなくてOKです。
ご家庭も気にしなくてOKです。

講師は・・・ダメなんですよ。

何が問題かというと
指導中の生徒とのやりとり。

生徒の話すコトバが
伝えたいことと一致していないケースがあるという点。

ん、なんかヘン、ズレてる？？？
とこちらが気づけばよいのですが

生徒が考えている内容と話す内容がズレているのに
偶然にも筋が通ってしまい
気づかずにスルーしてしまうことも。

生徒にしてみれば
なんだかしっくりこない気持ち悪さが残る。

そうならないように
アンテナを張って
生徒の話を聞く必要があるんです。

授業終わったら
心地よい疲労感

ときには
消耗しすぎて抜け殻に。

う～ん
生易しくはないですね。

　コトバの問題は避けて通れない！？　～　その3　

コトバによる問題文の読み取りのハンデは
時期が来ればほぼ解消することがわかっている

とさきほど言いましたが

時期が来るのを待つのも
ご家庭にしてみれば
ハラハラ、ドキドキ
がつきまとうわけです。

そこで
早い段階で得点源になる単元を作りたい。

何かひとつ得点源になる単元を作ると
生徒はそれだけで自信をつけ安心します。

算数の指導をすべて任されるのであれば
真っ先に取り組むのは

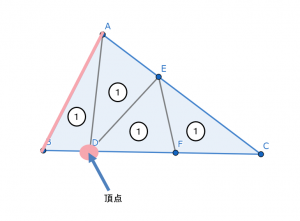
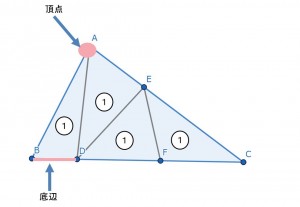
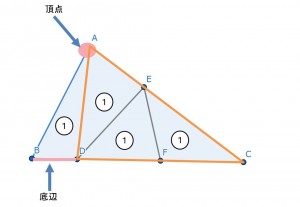
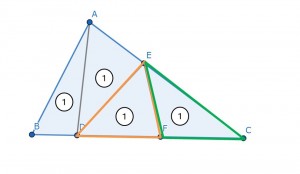
平面図形の強化

理由は
問題文にあまり影響されない単元だから。

志望校で出題される平面図形の特徴をおさえ
徹底的に演習を積み重ね
早期完成を目指す。

これまでドクターだけにお通いの帰国子女の指導において
この方針で進めて失敗したことがないので
おそらくは正しい方法論なのでは思っています。