015 放散虫：Z^3+0.5画像のフラクタル性(その4)

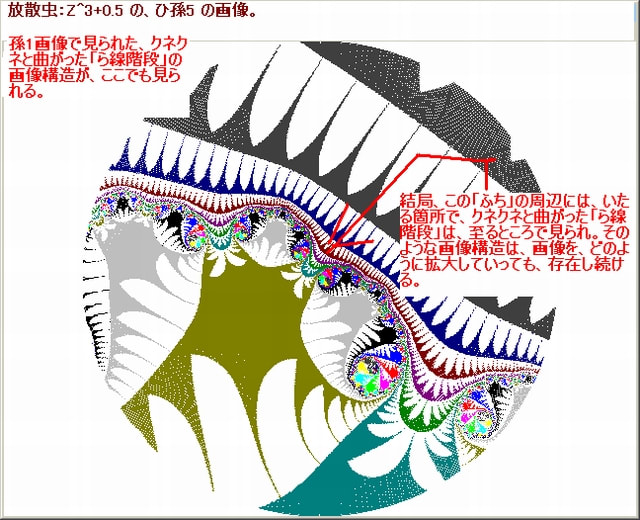
下図は、前画像014で示した孫1画像である。この画像の中の5箇所の部分(A～D)を拡大する。それらの画像を便宜上、それぞれ「ひ孫画像1」～「ひ孫画像5」と名付ける。なお各画像の説明は各画像に書いてある。








------------------------------------------------------
記事012より今迄見てきた画像から下記のことが言える。

放散虫：Z^3+0.5 画像の”内臓”部の画像は、3個の同一な画像から構成されている。
そして其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されている。
そして更に其の3個の画像自体も、それぞれ、自己相似な3個の画像から構成されていて・・・・。このような画像構造が永遠に続いている。

そして又その3個の画像には、それぞれ、1点へと収束していくクネクネと曲がった「ら線階段」が無限に存在する、ということである。

即ち、3個の画像を、どのように拡大していっても、3個の自己相似な画像が永遠に存在する。そして其の画像は、1点へと収束していくクネクネと曲がった自己相似な「ら線階段」が無限に存在する、ということである。

この無限の自己相似性の二重構造が、放散虫：Z^3+0.5　の「内臓」部の画像構造になっている。これは何とも複雑な構造だ。

こんな複雑な構造自体を知らなくても、放散虫：Z^3+0.5　の「内臓」部の画像を見て何となく奇妙で面白い感じをもつのは、我々が此の画像の或る秩序をもった複雑性を直感的に感じ取っているからだろう。