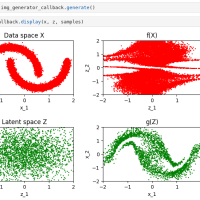
The Method of Moments in Electromagnetics の 3.3章で、3.23式から3.25式への部分で理解に手間取ったのでメモしておく。
まずは、Maxwellの方程式から、スタート.
角速度ωで振動している電磁場を対象に、複素数であらわすと
(3.1)
(3.2)
(3.3)
(3.4)
式(3.1)の両辺の回転(curl)を取って、式(3.2)を代入し、電界強度 E に関する項を右辺に集めて、ベクトルの公式を適用。
式を簡潔にするため、波数 k も使って書くと次の式が得られる
(3.23) - %5Ctriangledown %5Ctimes M)
ここで、この式の意味するところを考えてみる。この式のEやJやMは、空間の任意の点での電界強度、電流密度、磁流密度(の位相と振幅を複素数で)を表しているが、一点でなく空間全体に広げ、空間全体の電界強度の分布、電流密度、磁流密度の分布/場 と見てもよい。
つまり E とは、ある位置 r に対してその位置の電界強度を与える関数 E(r) をあらわしていると読む。
すると3.23式の右辺は、電場を引き起こす源の分布、左辺はそれによって引き起こされる電界の分布の満たすべき条件とも取れる。

ここで、この分布fが、 = - %5Cdelta (r{}', r)) だったらどうかを考える。
だったらどうかを考える。
つまり、位置 r' のみに電磁流があり、その値は3.23式の右辺に当てはめると-1になる場合である。
で、なにかある関数 G(r) が、3.29式を満たしていたとすると、その関数G(r)は、位置r'のみに電磁流があるときに位置rの電界強度を与える関数と言える。
G は、位置r'のみに電磁流があるときの空間全体の電界強度分布を表すと。もちろん、Gはr'が異なればGの形も異なるので、G(r,r') と書くのが適切。なので、式3.24となる。
式3.24を満たすグリーン関数 G(r,r')が得られれば、位置r'のみに電流密度J(r'), 磁流密度M(r')があったときの位置rの電界強度は
 = - G(r,{r}')%5Cleft [ j%5Comega %5Cmu J%5Cleft ( r %5Cright )-%5Cfrac{1}{j%5Comega %5Cepsilon }%5Ctriangledown %5Cleft ( %5Ctriangledown %5Ccdot J%5Cleft ( r %5Cright ) %5Cright )-%5Ctriangledown %5Ctimes M%5Cleft ( r %5Cright ) %5Cright ])
解きたいのは、電磁流は分布していている場合だが、電磁気は線形なので空間全体の全ての点の分を足し合わせればよい。つまり上記の式を全空間で積分してやればよい。
 = - %5Cint_{V}^{ } G(r,{r}')%5Cleft [ j%5Comega %5Cmu J%5Cleft ( r %5Cright )-%5Cfrac{1}{j%5Comega %5Cepsilon }%5Ctriangledown %5Cleft ( %5Ctriangledown %5Ccdot J%5Cleft ( r %5Cright ) %5Cright )-%5Ctriangledown %5Ctimes M%5Cleft ( r %5Cright ) %5Cright ] d{r}')
で、これをちょこっと変形、整理すれば、3.25式となる。
(1) Walton C. Gibson,The Method of Moments in Electromagnetics Second Edition,CRC Press,2015. ISBN978-1-4822-3580-7
まずは、Maxwellの方程式から、スタート.
角速度ωで振動している電磁場を対象に、複素数であらわすと
(3.1)
(3.2)
(3.3)
(3.4)
式(3.1)の両辺の回転(curl)を取って、式(3.2)を代入し、電界強度 E に関する項を右辺に集めて、ベクトルの公式を適用。
式を簡潔にするため、波数 k も使って書くと次の式が得られる
(3.23)
ここで、この式の意味するところを考えてみる。この式のEやJやMは、空間の任意の点での電界強度、電流密度、磁流密度(の位相と振幅を複素数で)を表しているが、一点でなく空間全体に広げ、空間全体の電界強度の分布、電流密度、磁流密度の分布/場 と見てもよい。
つまり E とは、ある位置 r に対してその位置の電界強度を与える関数 E(r) をあらわしていると読む。
すると3.23式の右辺は、電場を引き起こす源の分布、左辺はそれによって引き起こされる電界の分布の満たすべき条件とも取れる。
ここで、この分布fが、
つまり、位置 r' のみに電磁流があり、その値は3.23式の右辺に当てはめると-1になる場合である。
で、なにかある関数 G(r) が、3.29式を満たしていたとすると、その関数G(r)は、位置r'のみに電磁流があるときに位置rの電界強度を与える関数と言える。
G は、位置r'のみに電磁流があるときの空間全体の電界強度分布を表すと。もちろん、Gはr'が異なればGの形も異なるので、G(r,r') と書くのが適切。なので、式3.24となる。
式3.24を満たすグリーン関数 G(r,r')が得られれば、位置r'のみに電流密度J(r'), 磁流密度M(r')があったときの位置rの電界強度は
解きたいのは、電磁流は分布していている場合だが、電磁気は線形なので空間全体の全ての点の分を足し合わせればよい。つまり上記の式を全空間で積分してやればよい。
で、これをちょこっと変形、整理すれば、3.25式となる。
(1) Walton C. Gibson,The Method of Moments in Electromagnetics Second Edition,CRC Press,2015. ISBN978-1-4822-3580-7