数学的実在とは－幾何学－12－原論と基礎論(10)

　前回の続きです。

　連続の公理は２つの公理からなりますが、どちらも直線上の点に関する命題、すなわち１次元空間の命題です。

Ⅴ1.(計測の公理あるいはアルキメデスの公理) ABおよびCDを任意の線分とすれば,直線AB上に有限個の点A1,A2,A3,…,Anが存在して,線分AA1,A1A2,A2A3,…,A(n-1)Anが線分CDに合同にして,かつBがAとAnの間にあるようにすることができる.

　この定理はすなわち次のようなことを言っています。
・直線上のどんな２点間も合同な線分を有限個連ねて覆い尽くせる
・直線上のどんな遠くの点も合同な線分を有限個連ねて追いつける

　なんだか当たり前に見えますが、アルキメデスの公理が成立しないモデルを見てみると意味がわかりやすいかも知れません。例えば普通の距離が定義されている数直線上で、原点Oからの距離が[ω]である適当な点ωを取ります。次に原点Oとωの間の点Aについて、原点Oからの通常の距離を[A]として、新しい距離Le(OA)を次のように定義します。
　　Le(A) = １／([ω]-[A])

　そして２点C,D間の距離(線分CDの長さ)は次のように定義します。
　　Le(CD) = |Le(D)-Le(C)|

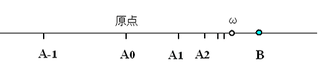
　そしてLe(線分)が等しいこととして線分の合同を定義すれば、ωを挟んだ２点A,Bについてはアルキメデスの公理が成立しないことは明らかでしょう。原点Oから見るとωはいわば無限遠点になっているのです。
　また01/15記事"幾何学のモデル－非ユークリッド平面－"で紹介したケイレイ=クライン結合平面ではユークリッド平面上のひとつの円の中にモデルを作り、この円がモデルにおける無限円直線になっていますが、モデル内の直線を円外に延ばしてしまえば、この直線上ではアルキメデスの公理が成立しないと見なせます。

　端的に言えばアルキメデスの公理により、直線上の全ての点から実数内部(実数のある部分集合)への1:1写像が保証されます。実際、アルキメデスの公理というのは実は実数や有理数のような順序体、つまり順序付けられて２つの演算の積と和が定義された集合についての公理でもあります。アルキメデスの公理が成立する順序体をアルキメデス的順序体といいますが、これは乱暴に言えば無限大より大きい要素(元)を持たない順序体のことです。

　さて連続の公理の２番目です。
Ⅴ2.(一次元の完全性公理) 一直線上にある点は,線状順序(定理6),合同公理の第1番,およびアルキメデスの公理(すなわち公理Ⅰ1,Ⅱ,Ⅲ1,Ⅴ1)をたもつ限りでは,もはやこれ以上拡大不可能なる点の集まりをなす.

　「拡大不可能」という意味は、これ以上の点を１つでも加えると、ここに挙げた公理の全てを満たすことはできなくなるという意味です。完全性については野崎昭弘が『不完全性定理』のなかで「私が知っているだけでも5～6通りの違った意味がある」と書いています(01/29記事")が、この拡大不可能という性質もその一つでしょう。ゲーデルの定理などでの完全性(completeness)というのは命題について述べた言葉ですが、ヒルベルトの公理系での"completeness"は、点や直線、面といった要素について述べた言葉だということは明確な違いです。

　ちなみにこの公理でいう「完全性」という言葉は「完備性」と訳されていることが多いのですが、どちらも英語では"completeness"です。よく知られているのは「実数の完備性」という言葉ですね。これは乱暴に言えば、実数全ての集合には隙間がなくてもはや余分な元を入れることができないということを意味します。正確な定義にはいくつか異なるものがあるようです。完備性を持つアルキメデス的順序体を完備順序体とよびますが、完備順序体は本質的に1つしか存在しないことが証明されています。端的に言えば、一次元の完全性公理により全ての実数と直線上の全ての点を1:1に対応させられることが保証されます。要するに我々がよく使う「数直線」というものの存在が保証されるのです。

　　　続く

－－－－補足－－－－
1) 完備順序体に関しては、大田春外『はじめよう位相空間』日本評論社(2000/12),p152 の記載を参考にした。
2) 完全と完備について興味深い議論があった。
http://d.hatena.ne.jp/MarriageTheorem/20081116/1226808794
　"complete"の訳は「完備」か「完全」か (2008/11/16)
http://d.hatena.ne.jp/wd0/20080825/a
　不完全性定理は「現代科学の限界」なるものを示してはいない (2008/08/25)
3) 英語では"complete"と"perfect"のニュアンスはどう違うのだろうか。なんとなく"complete"と完備、"perfect"と完全ないし完璧が対応しそうだが。