方程式  (n:3以上の自然数)に自然数解(x,y,z)は存在しない、というフェルマーの最終定理は、1995年にワイルズにより最終的に解決をみた。
(n:3以上の自然数)に自然数解(x,y,z)は存在しない、というフェルマーの最終定理は、1995年にワイルズにより最終的に解決をみた。
n=3の場合は18世紀にオイラーにより既に証明されていたとのことである。しかし、否定的解決というのは、どうも面白くない。「存在しない」より「存在する」方がなんだか有難い。ここでもラマヌジャンが鬼才を発揮してくれた。

は言わずと知れたタクシー数である。これは2通りに自然数の3乗の和であらわされる最小の数、というように説明されるが、

と書くと、もう少しでn=3の場合のフェルマー方程式の解になることがわかる。これだとなんだかな、という感じだが

くらいになると、「ウーム、惜しい」とうめきたくなる。
ラマヌジャンは、このような例が無数にあることを示してくれた。まず、 を以下により定義する。
を以下により定義する。

この時、 が成り立つ。ちなみにnが小さい時のの値は次のようになる。
が成り立つ。ちなみにnが小さい時のの値は次のようになる。

(以上、出典:「ひとけたの数に魅せられて」、マーク・チャンバーランド著、川辺治之訳、岩波書店(2016)のP107 )
どうして、こんな式を思いついたんだろうと誰もが不思議に思う。例えば、Hirschhorn氏は、以下の論文[1]、[2]、[3]でラマヌジャンはおそらくこのようにして導いたのだろうと書いている。
[1] M.D.Hirschhorn, An amazing identity of Ramanujan, Math. Mag. 3 (1995), 199-201
[2] M.D.Hirschhorn, A proof in the spirit of Zeilberger of an amazing identity of Ramanujan,
Math Mag. 4 (1996), 267-269
[3] M.D.Hirschhorn, Ramanujan and Fermat’s Last Theorem, Austral. Math. Soc. Gazette.,
Vol.31, pp.256–257, 2004.
2通りに自然数の3乗の和として表わされる自然数にはパラメーター解があることが知られている。[3]では、パラメータ解から、上で示したような近似解列を導いている。
本ブログの「タクシー数」でそのようなパラメーター解を示したので、[3]の例に倣って近似解列を求めてみる。

が、そのパラメータ解である。
ここで、右辺の2項目が±1となり、残りの3項が正数の3乗となるような整数u,vの列を作れればよい。
 であり、行列式が±1の2行2列行列
であり、行列式が±1の2行2列行列  で
で 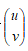 を変換しても、式の値は変わらないことに注意する。
を変換しても、式の値は変わらないことに注意する。
 かつ
かつ  に注意すれば
に注意すれば

となる。 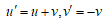 として、最初のパラメータ解を変換すると
として、最初のパラメータ解を変換すると

より、
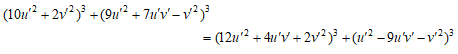
となる。
ここからは、M.D.Hirschhorn [3]とまったく同じであるが、書いてみると
 とおき、数列
とおき、数列  を
を
 で定める。この時、
で定める。この時、
 とおくと
とおくと

実は、この式はnが負でも成立することがわかる。但し、その場合は  必ず負となるので
必ず負となるので

とすれば良い。
絶対値が3以下のnについて表に示す。
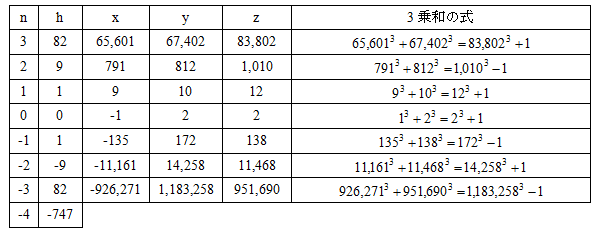
結局、「タクシー数」で見つけたと思ったパラメータ解は、既知のものであることが分かった。
上の例は、  が肝であったが -1 以外の数で同様の現象があるか探してみた。
が肝であったが -1 以外の数で同様の現象があるか探してみた。

に戻り、 に着目し、
に着目し、  とおき、数列
とおき、数列  を
を
 で定める。この時、
で定める。この時、
 とおくと
とおくと

nが7以下の例を下表に示す。

パラメータ解において、ターゲットとする2次形式のuの2乗の係数が1であれば、vの2乗の係数 t について、同様なことが成立する。

というパラメータ解もある。u=1,v=0とすると

が得られる。このパラメータ解について、同様の近似解を求めようとしたがうまくいかなかった。2つの3乗数の和で2通りに表される解はすべて何らかのパラメータ解であらわされるのか、パラメータ解で他にフェルマー方程式の近似解列を発生するものがあるのか、など次から次へ話題が浮かんでくる。
また、上記「ひとけたの数に魅せられて」に3乗以外でフェルマー方程式の近似解列がないか、という感想が書かれていたが、nを3より大きい自然数,x,y,zを相異なる自然数、cを整数として

となる絶対値最小のcは求められているのだろうか。求められていないとすれば、みんなでcを探す競争をしても面白いかもしれませんね。
このようなことを考えていると、ディオファントス方程式についていろいろ学ばないといけないと思いますが、どなたか一緒に勉強しませんか。

 ここでm’は平方因子を持たない自然数。aは有理数。
ここでm’は平方因子を持たない自然数。aは有理数。 







 さらには、
さらには、 についても、mが何であっても無限個の有理数解を有する。
についても、mが何であっても無限個の有理数解を有する。









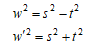 を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。 したがって、
したがって、 これが成立するのは
これが成立するのは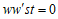 の場合に限る。
の場合に限る。 とすると、
とすると、 である。
である。 とすると
とすると となり、
となり、 である。
である。 とすると、
とすると、 となる。
となる。 とすると
とすると となり、
となり、 について
について を満たす有理数は、
を満たす有理数は、 の場合のみである。
の場合のみである。 よって、
よって、 より、上に述べたことより
より、上に述べたことより である。
である。 のときに限る。
のときに限る。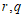 については、
については、 は
は  と非自明の例がある。
と非自明の例がある。 …(A)
…(A)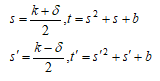
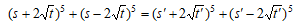
 とすると5乗和が等しいので
とすると5乗和が等しいので 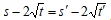 これより
これより 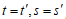 となり矛盾。
となり矛盾。 とすると
とすると 両辺を足して
両辺を足して  となり矛盾。
となり矛盾。 とおくと
とおくと  であるので(A)は、
であるので(A)は、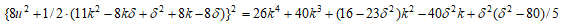
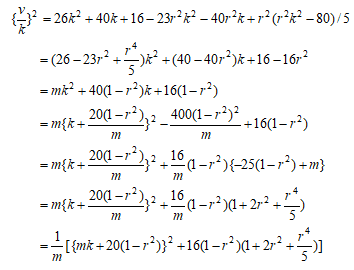

 とおくと、上の等式は
とおくと、上の等式は となる。この有理数解が存在するとしてその一つを
となる。この有理数解が存在するとしてその一つを  とすると、一般解は、有理数gを用いて
とすると、一般解は、有理数gを用いて である。よって
である。よって より
より  より
より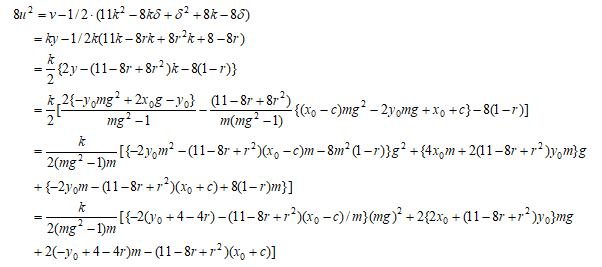

 より
より したがって、
したがって、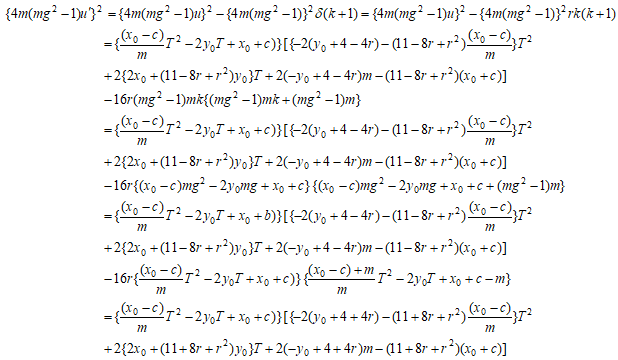
 と
と  の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。
の右辺はともにTの2次式の積である。積の左項は同一、右項はrの関数と見た時、rを-rに置き換えた式となっている。この式の左辺をY'とすれば、Y'、Tに関する4次式の有理点を求めればu'が求まる。 の解を具体的に求め、u,u'が有理数となる場合を探してみる。
の解を具体的に求め、u,u'が有理数となる場合を探してみる。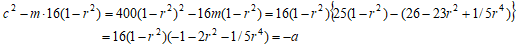
 が有理数の平方のとき、
が有理数の平方のとき、  は解である。
は解である。
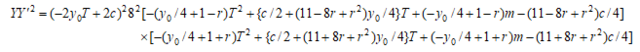
 にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。
にも共通T座標をもつ有理点がある。結局、これらTについての3つの3次式または4次式のうち2つに共通のT座標を持つ有理点が見つかれば有理数の5乗和で2通りに表される例が見つかることとなる。 とする。
とする。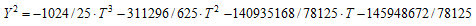
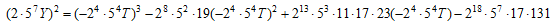
 が負となる解が得られる。したがって、実2次体の例にはならない。
が負となる解が得られる。したがって、実2次体の例にはならない。 なる解が得られる。
なる解が得られる。 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、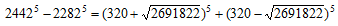
 とする。
とする。 の
の  の係数
の係数  が平方であれば、この4次式は有理点を有する。
が平方であれば、この4次式は有理点を有する。  とおくと、
とおくと、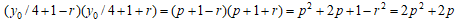
 つまり
つまり 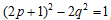 の有理数解を求めればよい。この一般解は、
の有理数解を求めればよい。この一般解は、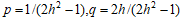 である。一方、
である。一方、 なので、
なので、 ともパラメトライズされる。
ともパラメトライズされる。 より
より  を得る。
を得る。 とすれば、4次式が有理点を有することになる。
とすれば、4次式が有理点を有することになる。 とおけば、
とおけば、 よって、
よって、
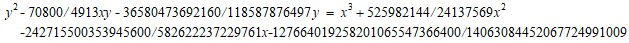
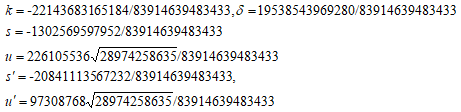
 をもとめ、共通因子を排して、
をもとめ、共通因子を排して、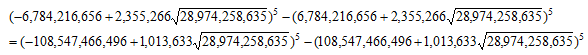
 の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。
の有理点のうち、Yの有理点となるものがないか、いくつかのrについて計算したが、なかなか有理点にはなりそうもない。やはりあてずっぽうではうまくいかない。
 (n:3以上の自然数)に自然数解(x,y,z)は存在しない、というフェルマーの最終定理は、1995年にワイルズにより最終的に解決をみた。
(n:3以上の自然数)に自然数解(x,y,z)は存在しない、というフェルマーの最終定理は、1995年にワイルズにより最終的に解決をみた。


 を以下により定義する。
を以下により定義する。
 が成り立つ。ちなみにnが小さい時のの値は次のようになる。
が成り立つ。ちなみにnが小さい時のの値は次のようになる。


 で
で 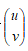 を変換しても、式の値は変わらないことに注意する。
を変換しても、式の値は変わらないことに注意する。 かつ
かつ  に注意すれば
に注意すれば
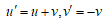 として、最初のパラメータ解を変換すると
として、最初のパラメータ解を変換すると
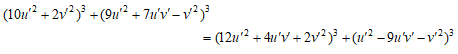

 を
を で定める。この時、
で定める。この時、

 必ず負となるので
必ず負となるので

 が肝であったが -1 以外の数で同様の現象があるか探してみた。
が肝であったが -1 以外の数で同様の現象があるか探してみた。
 に着目し、
に着目し、  とおき、数列
とおき、数列  を
を で定める。この時、
で定める。この時、




