メモ6で p=113のとき、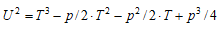 の位数∞の有理数解について記した。これは、本ブログの4次楕円曲線 その2 で述べた予想
の位数∞の有理数解について記した。これは、本ブログの4次楕円曲線 その2 で述べた予想
(予想)
素数pがp≡±1 (mod8)のとき、次の楕円曲線C
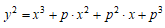
の有理数解のなすアベール群のランクは1である。
に関連していることを示した。ここでは、ある条件で得られるp≡1(mod8) の素数について、楕円曲線
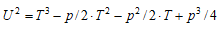 (A)
(A)
の位数無限大の有理数解を求める方法を記す。
楕円曲線(A) は

とも書ける。ここで、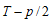 と
と  がともに有理数の平方になるようなTが求まれば楕円曲線(A) の有理解が求まることになる。そこでCocalcを用いてpが小さい場合に生成元及びその2倍を求めてみた。
がともに有理数の平方になるようなTが求まれば楕円曲線(A) の有理解が求まることになる。そこでCocalcを用いてpが小さい場合に生成元及びその2倍を求めてみた。

このように生成元も若しくはその2倍について、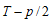 及び
及び  がともに有理数の平方になることが期待される。そこで、正の有理数a,bを用いて
がともに有理数の平方になることが期待される。そこで、正の有理数a,bを用いて
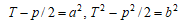
とおき、Tを消去すると
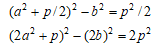
 と
と  の分母の最小公倍数を δ とすれば
の分母の最小公倍数を δ とすれば
 ただし、
ただし、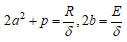
である。よって、この方程式の整数解 をR,E,δ のうち 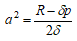 を満たすものを求めれば楕円曲線(A) の有理点が求まることになる。
を満たすものを求めれば楕円曲線(A) の有理点が求まることになる。
上の表で 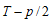 及び
及び  が ともに有理数の平方となる有理点についてR,E,δを求めδ, R+E, R-Eを記したのが下表である。なお、δ, R, Eはすべて自然数とする。
が ともに有理数の平方となる有理点についてR,E,δを求めδ, R+E, R-Eを記したのが下表である。なお、δ, R, Eはすべて自然数とする。
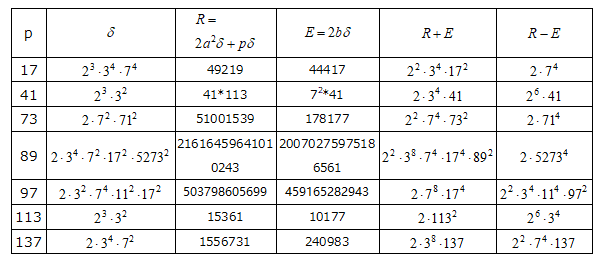
この表より 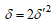 と書けることが期待される。そこで以下
と書けることが期待される。そこで以下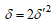 と仮定する。
と仮定する。
そのとき、
 の自然数解 R,E,δ について
の自然数解 R,E,δ について 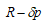 が平方数であれば
が平方数であれば
 は楕円曲線(A)の有理点である。
は楕円曲線(A)の有理点である。
まず、
RとEが互いに素な場合、 の自然数解 R,E,δ は自然数m,nを用いて
の自然数解 R,E,δ は自然数m,nを用いて

と書けることに注意する(RとEが素でない場合について、最後の(追記:2019.5.12)を参照)。
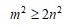 のとき、
のとき、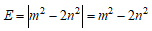 より
より

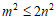 のときは、
のときは、

である。したがって、R+EおよびR-Eは平方数と平方数×2のペアであることがわかるが、上表を見ると p=41及び113,137以外は、平方数がpの2乗を因子を含むことが特徴的である。p=41及び113,137の場合も生成元の2倍を用いればR+Eが平方数かつpの2乗の因子を含むことがわかる。そこで、以下の2つのケースを仮定して検討する (2x平方数の方がpの2乗の因子を含む場合は(追記:5.12)を参照)。
ケース1:R+Eが平方数でpの2乗の因子を含む
ケース2:R-Eが平方数でpの2乗の因子を含む
ケース1の場合:

なので、n=pn’ と分解される。したがって、pδ=2mnより、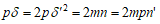 よって
よって
 この条件はmとn'が平方数であれば満たされる。
この条件はmとn'が平方数であれば満たされる。

より R-pδ が平方数であるための条件を考える。まず,自然数 α,βにより

とあらわされる場合を考える。例えばn及びmが奇数の場合である。上表の場合はそうなっている。なお、この場合はnが偶数のとき、mも偶数となるので、mとnは互いに素ではなくなる。
m>nとすれば
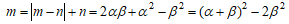
したがって、mが平方数とすれば、自然数c,dにより

となる。このとき、
 がp×平方数となればすべての条件が満たされることになる。
がp×平方数となればすべての条件が満たされることになる。
m<nのときは

したがって、mが平方数とすれば、自然数c,dにより

となる。このとき、
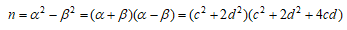 がp×平方数となればすべての条件が満たされることになる。
がp×平方数となればすべての条件が満たされることになる。
以上より、ケース1の場合は、以下の(x,y)が有理点となる。

ケース2の場合:

なので、n=pn’ と分解される。したがって、pδ=2mnより、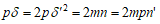 よって
よって
 この条件はm, n'が平方数であれば満たされる。
この条件はm, n'が平方数であれば満たされる。

より R-pδ が平方数であるためには,ケース1の場合と同様の考察により、自然数α,βにより

とあらわされる。ケース2の場合は、m>nであるので、
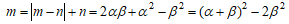
したがって、mが平方数とすれば、自然数c,dにより

となる。このとき、
 がp×平方数となればすべての条件が満たされることになる。
がp×平方数となればすべての条件が満たされることになる。
以上より、ケース2の場合は、以下の(x,y)が有理点となる。

上表にあげたのはp=97を除き、すべてケース1の場合であった。
上の議論を振り返ると、ケース2はケース1でをーEに置き換えた場合に相当する。また、m>nとm<nの違いはβを-β、つまり、dを-dに置き換えた違いに他ならない。
したがって、cを自然数、dを整数としたときに、
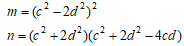 とおき、nがp×平方数の形になれば、以下の(x,y)が楕円曲線(A) の有理点となる。
とおき、nがp×平方数の形になれば、以下の(x,y)が楕円曲線(A) の有理点となる。
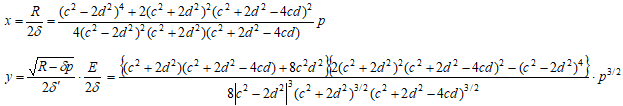
次に

とあらわされる場合を考える。上に記した場合と同様議論を行うと
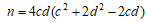 がp×平方数となればよい。このとき、以下の(x,y)が楕円曲線(A) の有理点となる。
がp×平方数となればよい。このとき、以下の(x,y)が楕円曲線(A) の有理点となる。
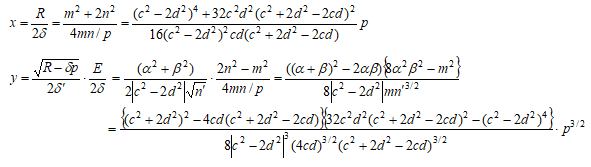
表1は、200以下のp≡1(8)の素数について、c,|d|が3000以下の時に、n'が自然数の平方になるケースを示したものである。なお、pに対応する(c,d)のペアは1つとは限らず、表はそのうちの一つのみ掲載している。あわせて上に示した式より有理点を具体的に求めた.

表2は、200以上1000以下のp≡1(8)の素数について、n'が自然数の平方になるケースを示したものである。なお、pに対応する(c,d)のペアは1つとは限らず、表はそのうちの一つのみ掲載している。
 がp×平方数の形をしている場合は、
がp×平方数の形をしている場合は、 である。
である。
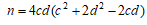 がp×平方数の形をしている場合も、
がp×平方数の形をしている場合も、 である。
である。
表からわかるように、1000以下の素数でもcまたは|d|はかなり大きな数となるようである。
このうち,857、977についてはCoCalcより求めた有理点より逆算した。また、929については、CoCalcでも求められなかった。

結局、自然数c, 0ではない整数dに対し
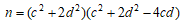 または
または  がp×平方数の形をしていれば、楕円曲線
がp×平方数の形をしていれば、楕円曲線  は位数∞の有理点を持つことになる。
は位数∞の有理点を持つことになる。
問題は、すべてのp≡1(8)の素数が、この条件を満たすかどうかである。
(2019.4.30 一部修正)
(追記:2019.5.3)
p=929のとき、CoCalcで gens() として楕円曲線(A) の有理点を求めるとうまくいかないが, これをgens(descent_second_limit=16)とすると解が求まった。limitのデフォルトは12 である。この解よりc,d,m,nを求め表2を補った。
(追記:2019.5.12)
・RとEが互いに素な場合、pで割りけるようである。その場合R/p, E/pをR,Eに置き換え同様の議論を行うと  がpx平方数の場合に帰着する。
がpx平方数の場合に帰着する。
・2×平方数の方がpの2乗の因子を含む場合についても、詳細は省略するが、  がpx平方数の場合に帰着する。
がpx平方数の場合に帰着する。



















※コメント投稿者のブログIDはブログ作成者のみに通知されます