メモ12 タクシー数と楕円曲線：rank 2以上の楕円曲線がどんどん出てくる

　タクシー数と楕円曲線の有理点が関係するだろうと前から思っていた。3次曲線

　　　

が、x，yの入れ替え以外の異なる2つの有理点を持てば、m×(ある整数の3乗)を2とおりの仕方で　整数の3乗　の和として表すことになるし、ランクが2以上の楕円曲線が得られるのではないかと思った。しかし、どのようにWeierstrass標準形に変換するのか考えたことはなかった。今回、その変換を求めてみたのでメモしておくことにする。
　但し、改めてSilverman・Tateの”Rational Points on Elliptic Curves”(以下[Sil]とする）をみると、その変換式やタクシー数についていろいろ書いてあることが分かった。

　　
　　なので、x+y=z , x-y=wとおくと、(*)は

　
　　
となる。これから両辺に12をかければ

　
　　
次に両辺を　zの3乗で割って

　
　　
さらに両辺に12mの2乗をかけて

　
　　
12m/zと36mw/zを改めてz,wとおくと

　
　　
であり、(*)は

　

とWeierstrass標準形に変換される。このとき逆変換は

　
　
で与えられる。

 ここで(*)の整数解と(**)の有理数解の間に何か関係ないだろうか。例えば(*)の整数解の個数、すなわち、自然数を異なる整数の組であらわす数Nと(**)の楕円曲線の有理点群のランクに関係があれば面白いと想像した。

gcd(x,y)=1　に限定した場合の解について[Sil]には以下が書かれている。

N= 2で自然数解とした場合の最小数m=1729がいわゆるラマヌジャンの逸話で有名なタクシー数
N=3 の場合、最小のmの整数解の場合と自然数解の場合は次のとおり。
　
N=4の場合は、そのような自然数解の存在は知られていないとのこと。
但し、wikipedia　に2003年に発見された以下の例が示されている。
 　
　
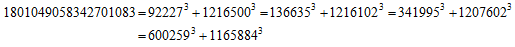
また、[Sil]のP151に以下の定理がある。
定理　mをm≧1なる整数。Cmを  なる3次曲線とするとき
mによらない定数κ>1があり、以下が成り立つ

　　

　この定理により、(*)を満たす整数解(x,y)でgcd(x,y)=1を満たすものが多ければ,(**)のあらわす楕円曲線の有理点群のrankも大きくなることがわかる。

　この定理からは、gcd(x,y)=1が満たされなければ、いくら(*)を満たす整数解が多くてもランクが大きくなるかどうかわからないが、例えば、ランク2以上になるためには、互いに素という条件がなくとも整数解が何個以上あればよいという数はないものかと考えた。一番安易な考えとして、mが異なる整数の3乗の和で表されれば、対応する楕円曲線(**)の有理点群のrankは2以上でないかと予想した。

 

であるので、試しにm=91，152，189，172９, 4104 についてCoCalcで計算してみると、189のときはランクが1となるが、それ以外では2となった。2016年10月29日に書いた本ブログの「タクシー数」で整数の3乗の和で2通りに表せるパラメータ解を示したが、これを用いてこの問題を部分的に解決したので以下に示す。

 

【説明】
恒等式

　

がなりたつので、

　

とおくとき、

　

に注意すれば

　
　

であるので、

　

は、u,vを有理数(整数)とすれば、楕円曲線Cの有理点(整数点）である。
もともとの恒等式がu,vに関する対称式であることに注意すれば

　

もCの有理点(整数点)である。したがって、P1 、P2が有限位数でなく、Z上で1次独立であることがいえればCの有理点のなす群のランクが2以上であることがわかる。

また　 　　とすると

　

である。

今、　２*R=0 (原点)となる点は0以外ないことに注意すれば、整数k1、k2について　
ｋ1*P1+k2*P2=0 (原点)　とするとき、k1 ,k2 はともに0、もしくは　ともに偶数ではないとして良い。
今、k1,k2がともに偶数ではないとすれば、n1*P1+n2*P2=2*R　ここでn1,n2は0または1でともに0ではない、となるCの有理点Rが存在する。したがって、P1、P2、P1+P2が有理点Rの2倍になることはないことがいえれば, k1=k2=0 となり、P1,P2は独立であることがいえる。

P=n1*P1+n2*P2=2*R、 P=(z,w), R=(x,y)とすれば2倍の式より
　 
　
これを整理して
　　　（A)

が整数解をもつことになる。このような整数解xが存在すると矛盾することを以下の順序で示す。

(1)　素数q≠2，3について、xのqべき指数eq(x)はzのqべき指数　eq(z)に等しいか大きい、もしくは、eq(12m)及びeq(z)は3の倍数、eq(x)は2の倍数である。

(2)　素数7 について、xの7べき指数e7(x)はzの7べき指数　e7(z)に等しいか大きい、もしくは、e7(z)は3より大きい。

(3)　素数q=2 または 3について、xのqべき指数eq(x)はzのqべき指数　eq(z)に等しいか大きい。

(4)　(1)、(2)より　mの7のべき指数が2以下であり、2、3以外にべき指数が3の倍数である素因子を含まない場合、xはzの倍数であるが、x=z　または2z,3z　でなければならない。

(5)　(4)と同じ条件のとき、ｘはz,2z,3zではありえない。

【(1)の説明】
P=P1、P2、P1+P2のとき,12mはそれぞれ

　　　

である。q≠2, 3なので、eq(12m)≧eq(z)　としてよい。

　

より、　

　

である。
　　eq(z) > eq(x) とすると　3eq(z) > 2eq(z)+eq(x) なので
　　4eq(x) ≥ min(eq(z)+3eq(x),2eq(z)+eq(x))
 さらに、
　　eq(z) ≥ 2eq(x) とすると、　eq(z)+3eq(x) ≤ 2eq(z)+eq(x) なので
　　　　4eq(x) ≥ min(eq(z)+3eq(x),2eq(z)+eq(x))＝eq(z)+3eq(x)　より
　　　　eq(x) > eq(z) となり矛盾。
　　eq(z) < 2eq(x) とすると　eq(z)+3eq(x) > 2eq(z)+eq(x) 　なので
　　　　4eq(x) ≥ min(eq(z)+3eq(x),2eq(z)+eq(x))＝2eq(z)+eq(x)　より
　　　　3eq(x) ≥ 2eq(z)　
　以上より、　常に　eq(x) ≥ 2/3*eq(z) 　

　また、

　

であるので、

　2eq(12m)+eq(x) ≥ min(4eq(x),eq(z)+3eq(x),e(z)+2eq(12m))
ここで、　

　eq(z)+3eq(x) < e(z)+2eq(12m) とすると、eq(x) ≤ 2/3*eq(12m)となる。

　eq(z)+3eq(x) ≥ e(z)+2eq(12m)とすると　
　　2eq(12m)+eq(x) ≥ min(4eq(x),eq(z)+3eq(x),e(z)+2eq(12m))
　　　　　　　　　= min(4eq(x),e(z)+2eq(12m))
　ここで　

　　4eq(x) > e(z)+2eq(12m) とすると　2eq(12m)+eq(x) ≥　e(z)+2eq(12m)　より　
　　　eq(x) ≥ eq(z) 
　　4eq(x) ≤ e(z)+2eq(12m)　とすると 
   　　2eq(12m)+eq(x) ≥ min(4eq(x),e(z)+2eq(12m))
　　　　　　　　　　 = 4eq(x)
よって、　eq(12m) ≥　3/2*eq(x) ≥ e(z)

したがって、eq(x) ≥ eq(z)　もしくは 　eq(12m) ≥　3/2*eq(x) ≥ e(z)　   である。

次に、

　eq(z) > eq(x) のとき、
　zの素因子qについて、12mのqべき指数は、ｚのqべき指数に等しい　　　（B) 

ことを示す。
　以下、背理法で（B) が成り立たつことを示す。
（B)が成り立たないとすると　 eq(12m)　> eq(z) 
P=P1のとき、
　

したがって、q≠2,3,7のとき、zがqを素因子にもつので、
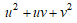　または　　　は　
と共通素因子qを持つ。
　
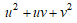であるので、　　と　　がqで割り切れれば、　u、vはqで割り切れる。これはu,vが互いに素に矛盾。また、
　
であるので、　と　　がqで割り切れれば　u,vはqで割り切れ、矛盾。

 

　次にP=P2のときは、u,vの対称性を考えて、(B)は成立しないとすると矛盾。

 

P=P1+P2のとき、
　
したがって、q≠2,3,7のとき、zがqを素因子にもつので、
  　または　　は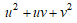　　
と共通素因子qを持つ。　これは上に述べたことと同様に矛盾。

以上より、（B)がいえた。
　つまり、　eq(z) > eq(x) 　とすると、zの素因子qについて
eq(12m) = 3/2*eq(x) = eq(z) である。これは、eq(12m)及びeq(z)が3の倍数、eq(x)が2の倍数であることを示す。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【(1)の説明終】

【2】の説明
　q=7のとき、上の説明で　e7(x) ≥ 2/3*e7(z) 　　はいえる。
したがって、e7(z)=0,1,2 のときは　e7(x) ≥ e7(z) である。　 
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【(2)の説明終】

【(3)の説明】
q=2のときは、u,vは互いに素なので、u,vともに奇数か、どちらか一方が奇数。
このとき、, 　,  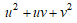　　はすべて奇数。
したがって、e2(z)=e2(12m)=2
　
より、
　
したがって、e2(x) ≥　1　である。e2(x)=1 とすると、 この不等式より　4e2(x) ≥　7
したがって、e2(x)　≥　2 = e2(z)

q=3 のときは、

　

よって、これらが3で割れないとき、
　e3(z)=e(12m)=1　　　P=P1またはP2のとき
　e3(z)=0, e(12m)=1　　P=P1+P2 のとき
これらが3で割れるとき　u≡v≡0,1,2 (mod3)　である。u≡v≡0　(mod3)の場合は,u,vが互いに素に矛盾するので除外してよい。
u=3s+1, v=3t+1 とすると
　
したがって、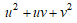　の3べき指数は1である。
　　の3べき指数が3以上であるためには
　　でなければならない。
　これは、mod3で考えると、(s,t)=(0,2), (1,0),(2,1) に限る。
これらの場合でも　3べき指数は4にはならないことを示す。
　mod3で(s,t)=(0,2)の場合、s,tをそれぞれ3s, 3t+2で置き換えると
　u=9s+1, v=9t+7 であるので、

　
　　
　(s,t)=(1,0)の場合、　s,tをそれぞれ　9s+4, 9t+1 として

　
　

　 (s,t)=(2,1)の場合、　s,tをそれぞれ　9s+7, 9t+4 として

　　
　

次に、　について考える。この3べき指数が3以上であるためには、
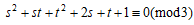　　でなければならない。
mod3で考えると、(s,t)=(0,1),(1,2),(2,0) でなければならない。
　この時も　　の場合と同様に　3べき指数は3となる。
以上q=3のときの　, 　,  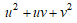　の3べき指数は次のとおりとなる。

したがって、e3(z)は6以下である。

今、e3(z)>e3(x)とすると

 

以上より、 3e3(z)>3e3(x) ≥ 6+2e3(z)
したがって、e(z) > 6 これは矛盾。ゆえに　e3(x) ≥ e3(z)　　　　　　　　　　　　【(3)の説明終】

 

 【(4)の説明】
(1)、(2)、(3)より、(4)の条件下で、xはzの倍数である。

次に、(A)式の左辺をf(x)としそのグラフを考え、xのとりうる範囲を考える。
　
　　　

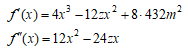
よりf''(x)=0となるのは　x=0　または　2z　であるので、zは必ず正であることに注意すれば、f’(x)はx=0で極大、x=2zで極小となる。　

　

であるので、f’(x)は　-zと0、0とz、2zと3zの間で実根を有する。これらをα, β, γ とすると
f(x)について、x<α で減少関数、α<x<βで増加関数、 β<x<γで減少関数、x<γで増加関数となる。

 

　

であるので、（A)の根ｘはz, 2z, 3zのいずれかである。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【(4)の説明終】

 

【(5)の説明】

　

であるので、z,2z,3zが（A)の根であるためには、

　

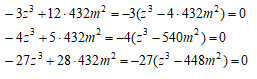
でなければならない。
次に、これらが成り立つのは　u+2v=0　または　u+v=0　のときに限ることをP=P1,P2,P1+P2の場合に分けて示す。

P=P1のとき、

　

であるので、u+2v=0のときに限り、3zは（A) の根となる。

P=P2の場合、u,vに関する対称性より　2u+v=0のときに限り、3zは(A)の根となる。

P=P1+P2の場合

 

　

 

であるので、u+v=0のときに限り、3zは（A) の根となる。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【(5)の説明終】
　以上で命題の説明は終わり。　　　　　　　　　　　　　　　　　　　　　　　　　　(説明終）