メモ11 ランク2以上の楕円曲線

　メモ8と9、10で　　q≠0,1の非負整数 

の位数∞の整数解、有理数解について考えた。メモ10では、q=38089のときにこの楕円曲線の有理点のなすアーベル群のランクが4以上であることをみた。これらの結果を踏まえ、ランクが2以上となる条件について検討したので、備忘録としてメモしておくこととした。

 

今、qを整数として

　　　

　C(Q)、C’(Q)をそれぞれ楕円曲線C,C'の有理点群　とする。 

また、メモ10の命題1と2より以下の①、②が成り立つ。

①　T=(1,0), T'=(-2,0)　とし、O, O'をC(Q), C'(Q)の零元とするとき

(a)　以下で定義される準同型　ψ：C’　→　C　があり、その核は｛O’, T’}である。

②　αを以下で定義される準同型　α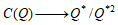：　とすれば、

　　　

　　　完全系列　　が得られる。

 

メモ10の最後に「ψ(C'(Q))の元が2C(Q)に含まれないことと上の4次方程式が2次方程式の積に分解することが同値であることを意味するのかもしれない。」と書いた。C(Q)のねじれ元のなす群がZ/2Zとすれば、

　　　　ここでr　はC(Q)のランク

なのでrが1以上であれば、　がいえれば、ψ(C'(Q))も2C(Q)も位数無限大の元を有するのでrは2以上と考えた(しかし、後でみるように、C(Q)={ψ(C'(Q))＋Tの生成する群｝の可能性もあるのでこれは成り立たない）。

　最初に、　を示すうえで有用と考えた以下の命題を示す(結局、あとで使わなかった)。

命題　qを非平方数とする。また、C,C’及びψ、αを上に示したとおり、φを以下で定義される準同型　φ：C　→　C’　とする。　また、T=(1,0)　とする。

 　

このとき、u≠1　とすれば

　　　かつ　　⇔　　　

　　　　(u,v)の2等分点(x,y)を求めるためのxの4次方程式が既約2次式の積に分解される。

(説明)

 ⇒　(u,v)=ψ((ｗ,z)) ∈ ψ(C'(Q))、(x,y)を(u,v)の2等分点とすると、

　　であるのでメモ4より

　

一方、上に記したことより

　

よって、

 

分母を払ってxの多項式として整理する。

ｘの3乗、2乗、x及び定数項は、それぞれ

 

となる。w=-2とすると(u,v)はC(Q) の零元となるのでw≠-2 よって、xは

 

を満たし、2次式の積に分解される。xが有理解を持てば、メモ4の2倍公式よりyも有理数。よって、(u,v)∈2C(Q))　となり矛盾。したがって、xの満たす4次方程式は既約2次式に分解される。

⇐　(u,v)=2(x,y)=ψ・φ(x,y)　である。(w,z)=φ(x,y)とおくと　(u,v)=ψ(w,z)　である。よって、(w,z)がC'の有理点であることが示せればよい。

　メモ10の命題1より

　

1番目の式より  よって　

2番目の式より  よって

　　

ｗが有理数でないとすると、w'=w+2　も有理数でない。仮定より　xはある2次体の元であるので　x∈Q(w')　としてよい。

　　ここでa,b,c,d∈Q

と分解とすると、

 

ｘの係数、定数項を比較して

　a+c=0,　　b+d=1

　ac-4bdq=-q,   bc+ad+4bdu=1

これら4式から、c,ｄを消去すると

　　　　　　①

　　②

qは非平方数なので、①より　a=0,b=1/2 となる。

したがって、②より　u=1　となるが　このときz=0、v=0

つまり、(u,v)=(1,0)　となり矛盾。よって、wは有理数である。

　より　w≠-2であれば　zも有理数。w=-2のときz=0　　　　(説明終)

 

次に、q≠0,1の非負整数とし、C(Q)のねじれ元はT=(1,0)のみ、かつ、ランクrが1以上の場合、つまりCが位数無限大の有理点を持つ場合、ランクが2以上となる条件を考えてみよう。このとき、α(T)∉ker(α)=ψ(C'(Q))なので、以下のいずれかが成り立てばよい。

 

　1．ψ(C'(Q))/2C(Q)の位数が4以上　

　2．C(Q)⊋ψ(C'(Q)とTで生成される群　かつψ(C'(Q))/2C(Q)の位数が2　

　3．C(Q)/｛ψ(C'(Q)とTで生成される群}　の位数が4以上　

 

さて、メモ8(ある楕円曲線の整数解) より、

楕円曲線C： 　 q≠0,1の非負整数　の位数∞の整数解はqが以下のときに限り存在する。

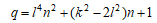　　　 　l,k: 自然数、n:0でない整数

このとき、　は位数∞の整数解。また、T=(1,0)は位数2の整数解であり、

 

以下、簡単のためにl=1としよう。　　である。

同じqを生成する異なる組 　について、上で求まる位数∞の有理点をとすれば、

　　　であれば

の代表するC(Q)/｛ψ(C'(Q)とTで生成される群}　の元は独立であるので、上の条件３よりランクは2以上である。

　であるのでが平方数でなければ　　はψ(C'(Q))に含まれない。

　　

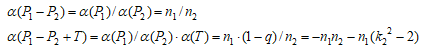
であるので、これらが平方数にならないようなを求めればよい。

今、2以上の自然数a,nbについて、(ak,n)と(k,nb) が同一のqを与えるとする。すなわち

　これを整理してnで割ると

　 　 

簡単のためにさらにk=1とすれば、

　が平方数でない　　(*)　　かつ、

　　(**)　

が成り立てばよいことになる。

(**)式は　

 

となる。

このa,bに関する不定方程式は,a=b=1という解をもつので、無限の有理数解をもつ。そのうちa≠bとなるともに1以上の整数の解a,nbを求めれば、同一のqを与える組(a,n),(1,nb)が得られる。

以下、具体例を2つの場合に分けて考えてみる。

【1】　nが平方数の場合

今、とすると、上式は

　となる。

　を解くと

　を得る。

つまり、組 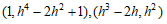は

同一の   を与える。かつ、n>1であれば　(*)を満たす。よって、以下が成り立つ。

 

ちなみに、ｈが小さい時のC(Q)のランクをCocalcで求めると以下の通り。

　　　h= 2, q=         73 ランク 2

　　　h= 3, q=　     4033 ランク 2

　　　h= 4, q=     50401 ランク ２

　　　h= 5, q=    331201 ランク ２

　　　h= 6, q=   1499401 ランク ２

　　　h= 7, q=   5306113 ランク 3

　　　h= 8, q=  15748993 ランク 3

　　　h= 9, q=  40953601 ランク 2

　　　h=10, q=  96049801　ランク 4

　　　h=11, q= 207345601 ランク 3

　　　h=12, q= 418141153 ランク 3

　　　h=13, q= 796565953 ランク 2

　　　h=14, q=1445862601 ランク 3

　　　h=15, q=2517580801 ランク 4

 

【2】　nが平方でない正整数の場合

　これまでの考察から

　　　は、解　X=2n-1,Y=2 を有するので、

　a=Y/2, nb=(X+1)/2 に注意すれば、Xが奇数、Yが偶数となるような解を求めれば、

(1,nb)と(a,n)　は同一の　をあたえるので、ランク2以上の楕円曲線が得られることになる。X0=2n-1, Y0=2 はそのような解なので、Q(√n）のノルムが1となる単数c+d√n　(c：奇数、d:偶数)について　　より　a,nbを求めれば、ランク2以上の楕円曲線が無数に得られる。

　なお、Q(√n）のノルム1の単数c+d√n　についてnが正であればc,dが自然数となるものは必ず存在し、c,dともに偶数ということはなく、c:偶数,d奇数であれば　　をとればよい。c:奇数、d：奇数の時はn=2のときは2乗、それ以外のときは4乗をとればよい。

　上で述べた条件１、２、3は排他的ではないが、今回は条件3の場合について具体例をみた。【1】、【2】で尽くされないランク2の楕円曲線も数多くあることに注意したい。例えばq<200以下でランク2以上となるのは以下のqである。

　31,51,73,79,90,119, 121, 130, 147, 166, 168, 179, 196