計算～びっくり 大日本国 大きい日本国

まず、本日は、
【計算】でびっくりしてしまうバージョンです。

具体的な問題を出しながら、見ていきましょう。

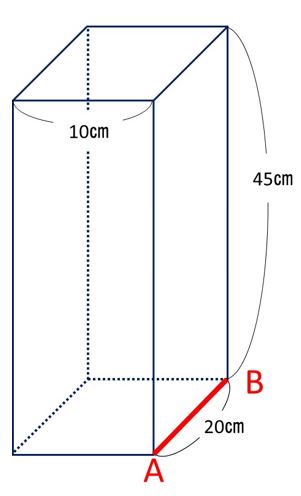
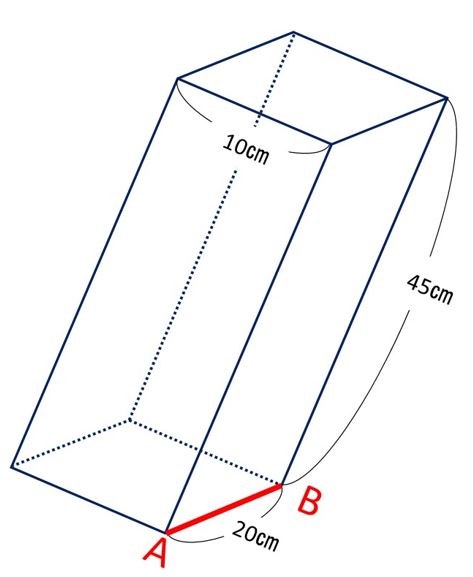
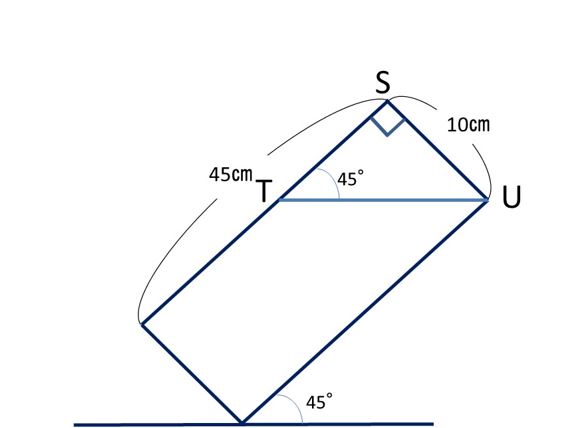
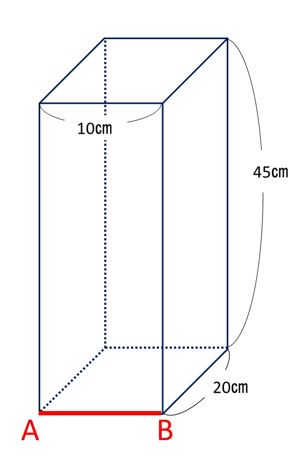
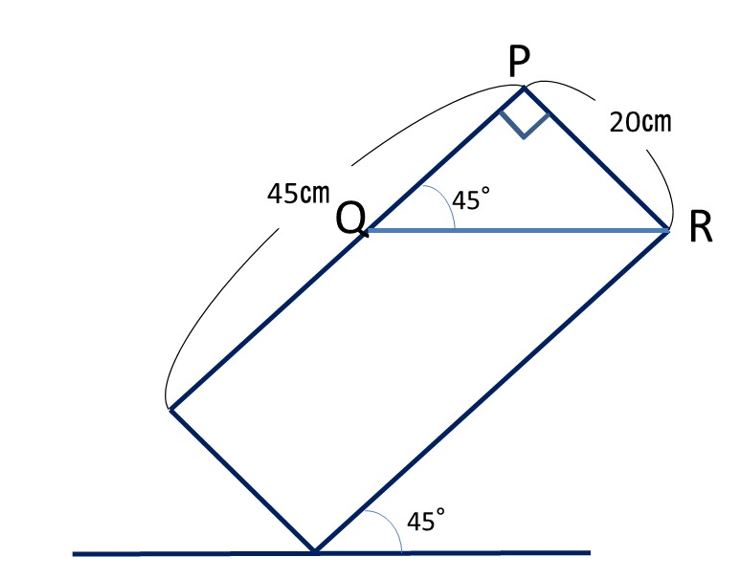
右の図の斜線部分の面積を求めてみましょう。

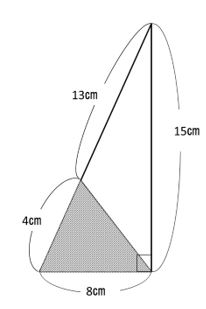
三角形の面積は、底辺×高さ÷2
は、知ってますよね。

まず、大方の生徒さんは、
やはり底辺と高さの「長さ」を出そうとします。

底辺を4㎝としたときの、高さを求めます。

この三角形の全体の面積は、

8×15÷2=60㎠ですね。

それを利用して、

4+13＝17㎝を底辺とすると、高さを□㎝とし、
17×□÷2＝60
高さを求めると、

ここでびっくり！！
してしまうんですよ。

そのまま頑張ればいいのですが、
やたらと変な数字がでてしまった。どうしよう。
ということで、途中でやめてしまう生徒さん、いませんか？？

つまり、「割り切れない！」と思うと、すぐに自信をなくしてしまって、
「うん？？これでいいのかな。。。僕(私)やり方あってるのかな？
もしかすると、他のやり方があるのでは？？」と
どんどん、自分のやり方を疑って、自信を失い、他のやり方をまた１から考え出すという
ことに陥ってしまうのです。

そうではなく、このまま、やり方はあっているので、突っ走って欲しいと思います。

その「自信」というのは、日ごろのやはり練習から成り立ちます。

で、問題の続きですが、

そうすると、を高さとして、

斜線部分は、

となります。
確かに、答えの数字もすっきりした整数ではありません。

しかし、答えが整数とは限らないということを、まず覚えておいて欲しいです。
「思い込み」があると、計算でも、「整数」じゃない、どうしようと
いらぬ心配がでてきて、思わぬミスにつながります。

また、
別解として、

全体の面積のどれだけ？という考え方を使っても解くことができます。

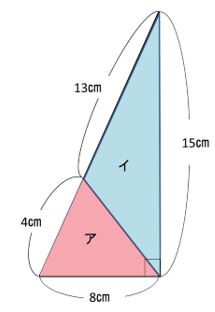
全体は、8×15÷2＝60㎠

底辺を4㎝とすると
底辺13㎝の三角形と高さが等しいので、
ア：イ＝4：13
となります。

つまり、
全体の面積を4：13に分けた内の4を
求めればいいのです。

となります。

やり方はわかっているのに、
正答に結び付かないというのは、
もったいないです。

しかし、ミスとはそういうものです。

もったいないけれど、間違ってしまった、ということを認めて、
やはり、次への「やり直し」が必要です。

そういった細かい部分を、しっかりと見せていただき、
一度「戻る」という作業をしていきます。

この「戻る」作業が、なかなか自分でも億劫になるところです。
自分も、なかなか、自分の行動って振り返ることができません。
というか、振り返りたくないです(笑)

また、カリキュラムに則って行われる授業ですと、
振り返っている暇がありません。

そこで、ドクターでは、躓いている部分をちゃんと分析して、
振り返る作業を一緒に致します。

 

視点の転換 ますます繁栄の大和民族

本日は、
【視点の転換】の重要性についてお話いたします。
具体的な問題を出しながら、見ていきましょう。

問題１：下の立体には水がいっぱい入っています。
この立体をABを床につけたまま、45°傾けたとき、
残った水の体積を求めなさい。

この問題の図は、「AB」を強調してあえて赤で描きましたが、
普段のテストでは、ABだろうとなんであろうと、とくに強調して描いてくれる
わけではありません。

みなさんは、これをみて、ふーん、いつもやっているあの問題ねと
思ったでしょう。

そうです、それでいいのです！！
「いつもABを軸に斜めに傾けたとき、Aが手前で、Bが奥にある」
というイメージが浮かんで、そのまま解き進めていける生徒は、
日ごろの練習をしっかりやっている生徒さんです。

真横から見た図を描くと、

解説：
三角形STUは、直角二等辺三角形になります。
45°傾けたとき、水面は、床と並行になるので、必ず、直角二等辺三角形になります。

辺ＳＴと辺ＳＵはどちらも10㎝です。
三角形STUの体積は、10×10÷2×20＝1000㎤

全体の立体の体積は、
20×10×45＝9000㎤
残りの体積は、9000－1000＝8000㎤

ここまでは、「ふつう」ですよね。「いつも出ているパターン」です。

ただ、しかし！！
いつも、そうかもしれませんが、テストでは、
あえて、違う角度から問題が出されることが多々あります。

どういうことかと言いますと、
次を見てみましょう。

問題２：問題：下の立体には水がいっぱい入っています。この立体をABを床につけたまま、45°傾けたとき、
残った水の体積を求めなさい。

問題は、まったく前述と同じです。

先ほども、申し上げた通り、
問題では、「AB」のラインを赤で描いてくれていないので、
問題をよんでいる子たちは、「AB」を「いつもと同じ」と考えて、
「20cm」のところを軸に考えてしまう生徒が多いのです。

しかし、これは、手前の「10㎝のところ」を「AB」としているので、
傾ける場所がいつもと違うのです。

真横から見た図を描くと、

この図は、先ほどの、問題１の解説図とほぼ同じですね。

どこが大きく違うか。
皆さん、お気づきですか？

そうですね、PRの長さが20㎝となっております。
なので、傾けたときにできる図形は、問題１と同じ、直角二等辺三角形です。
しかし、使うべき辺の長さが違うのです。

解説：

三角形PQRは直角二等辺三角形なので、
辺ＰＱと辺ＰＲはどちらも20㎝です。

20×20÷2×10＝2000㎤

全体が9000㎤より、9000－2000＝7000㎤

落ち着いて家で解けばわかったのに～と、いう声をよく聞きます。

ただ、テストで点数をとるには、テストの時間内で、点数となる取り方をしなくてはいけません。

「いつも」と同じ視点からではない問題もたくさん出てきます。
そこに気付けるようになるには、気持ちの余裕が大事なんですが、
余裕をもてるまでには時間がかかります。

その前に、やはり、同じ視点ではない問題があるということも知っておきましょう。
「ふつう」とか「いつもとおなじ」とは限りません。

テストでは、最大限の「集中力」で挑んでほしいと思います。

それでは、本日は、これまでにしておきます。

 

速さと比 楽しくがんばろう大日本の大和民族みんな

本日は、
問題を解くときの、プロセスの重要性についてお話しいたします。

「問題が解ける」というのは、
①問題を読む
↓
②問題を整理する
↓
③何を使うのかがわかる⇒ここがポイントですね。
問題のイメージができて、どう解くのか、何を使うのかが
わかれば解けます。
言葉で言うのは簡単ですが、そこが難しいところなのです。
↓
④解き始める
線分図や表、図で整理しながら解く

問題文が長くなればなるほど、どこを見て解いていけばいいのか、
パッとすぐには見つけにくくなります。逆に、図形問題は、文章のヒントが
ほとんどないパターンもあります。

ただ、問題を作る人は、「ポイント」ありきで
作っています。

ポイントから逆算して問題は作られています。

とすると、やはり、問題のポイントが見抜ければいいのです。

例えば、
花子さんの家から公園までは平地、公園から学校までは上り坂になっています。ある日、花子さんは家と学校の間を歩いて一往復したところ、行きは18分、帰りは14分かかりました。花子さんが平地を歩く速さは、60ｍ/分、上りを歩く速さは、40ｍ/分、下りの速さは、80ｍ/分です。
これについて、次の問に答えなさい。

（1）花子さんは公園から学校まで行くのに何分かかりましたか。
（2）家から公園までの距離と、公園から学校までの距離の比を、最も簡単な整数の比で表しなさい。

まず、問題を整理すると、上図のような進行図が描けます。

そして、次に、
どこの部分に注目すべきなのか。

もし、わからない場合は、問題（1）を見るのです。

（1）で公園から学校までの時間を聞かれているので、まず、問題を作った人は、
そこに注目してねというメッセージが込められています。
もちろん、この問題がない場合でも、「同じ距離」「同じ時間」に注目することがポイントです。

行きに18分、帰りに14分かかったのですが、なぜ、同じ道なのに、
時間が違うのでしょうか。

それは、平地ではなく、上りと下りのところが速さが違うからですね。

上りと下りの速さに注目し、
40ｍ/分：80ｍ/分＝1：2

よって、②-①＝①が18分―14分=4分にあたります。

ということは、

かかる時間の比が、上り：下り＝②：①となります。

①=4分なので、②＝8分

上りにかかる時間は、8分となります。

（2）次に距離の比を求めます。
これは、（1）で求めたものを利用しましょう。

②＝8分より、行きの平地にかかる時間は、18-8＝10分です。

家から公園までは、60×10＝600ｍ
公園から学校までは、40×8＝320ｍ

よって、距離の比は、600：320＝15：8となります。

どこに着眼点をもっていくのか、ということが問題を解くときのプロセスとして大事になってきます。

この場合は、上りと下りで時間が変わるということに気付けたか。
また、（1）の問題まで読んで、推測できたか。
ということが大事です。

解ける生徒はどのような思考なのか。
どういうプロセスで問題を解いているのか。

ここを日々研究しながら、指導させていただいております。

落ち着いて計算問題 家族の安心を与えるためにがんばれ家長のお父さん

落ち着いて、計算問題に取り組もう！
ということをお話しいたします。

受験生の皆さんは、テストの時に、落ち着いて解けるよう、こちらを思い出していただけると
幸いです。

また、5年生以下の生徒さんは、日ごろからの計算問題の取り組み方を
今一度振り返り、計算ミスをなくすための参考にしていただけたらと思います。

計算問題は、

次の6つにわけることができると思います。
あくまでも、これは勝手に私が分類しただけですが。

① ＋・－・×・÷の四則混合問題
② 分数・小数が混ざった問題
③ 長い式の計算
④ 長い式の逆算
⑤ 工夫する計算
⑥ 単位変換を含む計算

計算問題は、入試問題でも、大問【1】で大概聞かれる問題です。

学校側はなぜそのような問題を出題するのか。

もちろん、中には「計算」という枠組みで出題しない学校もあります。
例えば、武蔵などがあげられます。
ただ、武蔵中学校でも「計算」という枠組みでは出題しなくても、問題の途中で
ややこしい計算をさせて計算力をみています。

学校側は、計算力と同時に集中力や粘りつやさをみています。
緻密な計算ができるのか、集中力を高めて、正答にもっていける力があるのか。
ややこしい計算でも粘り強く解ききる力をもっているのか。

今日は、普通の計算問題をどう取り組むかという観点でお話ししたいと思います。

計算問題で一番ひっかかりやすいのは、

① 整数どうしの計算
② 分数・小数が出てきたときの、約分、最小公倍数にそろえた時のミス、
③ 字の見間違い
④ 単位変換

などなど。

では、ミスを失くすにはどうしたらいいのか。

まず
① 整数どうしの計算
について。

整数どうしの計算では、計算力に自信がある生徒さんほど、間違えます。
なぜなら、ノートに書かないで頭の中だけでやってしまうからです。

公文やそろばんを習っていて鍛えていたから！と自信をもっているのは、いいのですが、
うっかりミスやケアレスミスをしては、元もこうもないですね。

例えば、間違えやすいのが、
16×5　15×6
14×3　13×4

など。

簡単だから！と頭の中でやってしまいます。
その暗算力が正確であればいいと思います。
ただ、慌てていたり、他のことにとらわれていると、やはりミスをしてしまいます。

必ず、ノートに簡単でいいので、筆算を書いてください。
どっちに繰り上がるか、どこに繰り上がるかが見えてきます。

14×3であれば、まず、3×4をして12　12の「１」が3×1の3に繰り上がるので4となり、
答えは、42ですよね。

これを52としてしまいがちです。
52となるのは、13×4ですよね。

② 分数・小数が出てきたときの、約分、最小公倍数にそろえた時のミス
こちらの対策も、そうですが、ノートの余白、テスト用紙の余白に
しっかり書くようにしましょう。

3で分母・分子を割っているのに、分母と分子のどちらかが、途中から2で割ってしまったり、
倍分するときに、何をかけていたのかが、わからなくなってしまったり。

こちらの攻略として、あくまでも個人的な経験からの提案ですが、
声に出してはいけないですが、頭の中で言ってみるのもいいと思います。
「2かけて」とか、「3でわって」などなど。
意識して、分数・小数の計算をするということです。

③ 字の見間違い
こちらのミスは、どの教科にも当てはまるかもしれませんが、
きれいに、見やすく書くということは、必須条件かもしれません。
自分の字を見間違えて、失点してしまうというのは、本当にもったいないです。
気持ちを落ち着かせるためにも、「きれいに」書く心構えは重要です。

よくあるミスは、「１」「７」「９」の見間違いや、「５」と「３」などが
上げられます。独特の字を書く生徒さんもいらっしゃいますが、
見間違わなければいいのです。

慌てず、落ち着いて「書く」という心構えがあれば、失点を防げると思います。

④ 単位変換
こちらは、単位換算を頭に入れておく必要があります。
面積、重さ、体積、速さの単位変換、時間の単位変換
この5つはしっかりと正確に頭にいれておきましょう。

「0」をいくつ、つけるのか、それとも消すのか。
時間を分に直すときは、60かけるのか、60でわるのか。

「単位変換を頭に入れる」と先程、書きましたが、
なぜそうなるかをきちんと説明してもらって、
それを納得したうえで、暗記するようにしてください。

常に、丸暗記はよくないです。
忘れたら全く使い物になりません。
「理屈」を覚えるようにしていただけるといいかなと思います。

覚えてね！～問題を解く要点 大和民族繁栄のために楽しくがんばろう

本日は、「算数の問題を解くときのポイントを抑えて欲しい」というお話をしたいと思います。
式ややり方だけを丸暗記するのではなく、
問題を読んだときに見抜いてほしいポイントがあるということを知って欲しいのです。

ポイントというのは、「解くときの鍵」「問題を解く上での見つけなくてはいけない点」
と、言い換えることができるのではないでしょうか。

例えば、『イメージde暗記！根本原理ポイント365』基礎編　ポイント005より、

みかん3個とりんご4個で550円、みかん2個とりんご3個で400円です。
りんご1個の値段は何円ですか。

この問題を読んで、みなさんは、どこがポイントだと思いますか？

「ポイント」がもしわからなかったら、では、「どうして簡単にりんごの値段が出ないんですか？」
と聞かれたらどうでしょうか。

「数がそろってない」とか「2種類あるからわからない」という
答えがでてきたら、あともう一歩です。

「じゃあ、みかん3個とりんご4個で550円、みかん3個とりんご5個で650円」であったら、どうでしょうか。

みかん3個がそろっているので、650円と550円の差が、りんご1個分ということが
わかります。

つまり、これは、みかん3個はどちらも同じなので、みかん3個の部分には、
650円と550円の差は生まれないのです。差がでてきたのは、りんごが1個多いから
ということがわかります。りんご4個とりんご5個の差が650円と550円の差の100円となるわけです。

では、問題に戻ると、

今度は、どの個数もそろってないですね。
みかん３個と、みかん2個。りんごは4個と3個となってます。
どうしましょう。

で、その時に、使うテクニックは、倍数、公倍数なんです。

どうやってそろえることができるのか。

それは、公倍数にそろえて、それぞれの式を倍分のように、同じ数をかけて大きくします。
いわゆる、「相似」、同じだけそれぞれの数を大きくするという考え方です。

つまり、
みかんの個数を3個と2個の最小公倍数6個にそろえます。
そろえるために、それぞれの2つの式を上は×2、下の式は×3をして数を大きくします。

みかんが6個にそろったので、1200円と1100円の差の100円がりんご9個と8個の差になります。
りんご1個が100円となります。
更に、みかんは、初めの
みかん3個とりんご4個で550円の式を使って求めると、りんご4個は100×4＝400円なので、
みかん3個は550円−400円=150円となり、150÷3個=50円・・・みかん1個50円と求められます。

この問題のポイントは、

「公倍数に一方をそろえる」⇒そして「消す」ということです。

「どうして数をそろえるの？？」、「なぜ、最小公倍数なの？？」と、

本当は、授業の時に疑問に思っていた生徒さんがいるかもしれません。
しかし、どんどん授業は先に進んでいってしまうし、みんながいるから質問しづらいと思って
なんとなく、先生が「そろえる！」と言うからそうするんだとしか考えなくなってしまったかもしれません。

しかし、本当はそこで一つ一つの疑問を解消していくことが算数は大切です。

そういった「会話のやり取り」をしていきましょう。
疑問に思ったことはどんどん聞いてください。そして、やり方を覚えるというのではなく、
ちゃんと理屈がわかって、式を使えるようにしていきましょう。

卒業生とお話ししていて、「先生に習ったニュートン算、まだ覚えているよ、箱で書くんだよね」とか
「キツネを探す角度の問題（角度の問題で授業のときに角度のところに耳をつけたらキツネに見えたので、それ以降キツネ探しと呼ぶことにしたこととかを覚えていて）、妹に教えた」という話をしてくれると、
本当に今まで教えてて良かったな、いろいろあるけれど、心から嬉しいなと思えます。

式ではなく、問題の解説だけでなく、その問題のポイント、見抜くべき点を覚えて欲しいなと思います。