① 問題文をちゃんと読む。
② 何を使って解くかを見定めてから解き始める。
③ 問題文にでている条件を使っているか確認する。
短い文章の問題でも、長い文章の問題でも、
この3点に気を付けて問題文に当たってください。
それでは、本日は具体的に解いていきます。

(1)は、2つに分かれている文章の前半部分です。
以下の「ア」の部分から、

A店では、570個、
個数の比を求めて、
解きましょう。
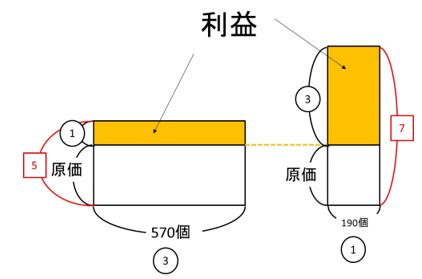
A店とB店の個数の比が570:190=3:1
より、利益が等しいということから、利益の比は、①:③
また、定価の比がA:B=1:1.4=5⃣:7⃣
となり、
5⃣=原価+①
7⃣=原価+③
より、7⃣-5⃣=③-①
2⃣=②
ということにより、□の比と○の比が同じになるので、原価は⑤-
A店の定価は⑤であるので、⑤÷④=1.25倍
それでは、次に(2)は、

イの部分を使って解き進めます。
(2)まずA店だけに注目して解いてください。
問題文の「2日目は、A店では品物Xを□
ここまでで、やはりまた、「同じ金額の利益」
とでているので、
A店は、⑤×0.95=4.75の定価で売ったことになります。
4.75‐4=0.75が2日目の利益の割合です。
1日目と同じ利益となってので、1日目の利益は①となるので、
①:0.75=4:3
よって個数の比は、3:4
3が570個に当たるので、4=760個
(3)今度は、
「B店では、
という文章のところを使って解きます。
(2)で求めたA店の個数を利用します。
A店は760個だったので、
そして、
1日目の定価が⑦なので、2日目は、⑦×0.7=4.9
4.9‐4=0.9・・・これが、
190×③+3000円=800×0.9
720-570=150・・・これが、3000円にあたるので、
①=20円
原価は、20×④=80円
皆さん、いかがでしょうか。
算数の問題も、文章を分析して、
そして、文章にでてきた数値、条件には○を付ける、線を引いて、
どの方針で解くかを見定めてから解くようにしましょう。
解き方は分かっているけれど、「気付けない」「
お悩みをよく聞きます。
問題文の読み方、条件の使い方、ここを個別で見ていきます。












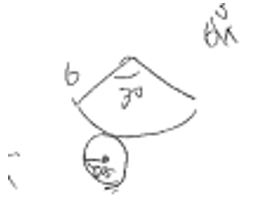

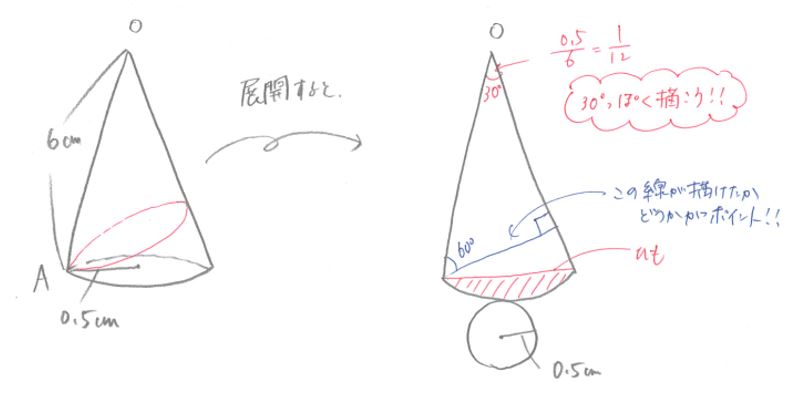
 より360÷12=30°
より360÷12=30°