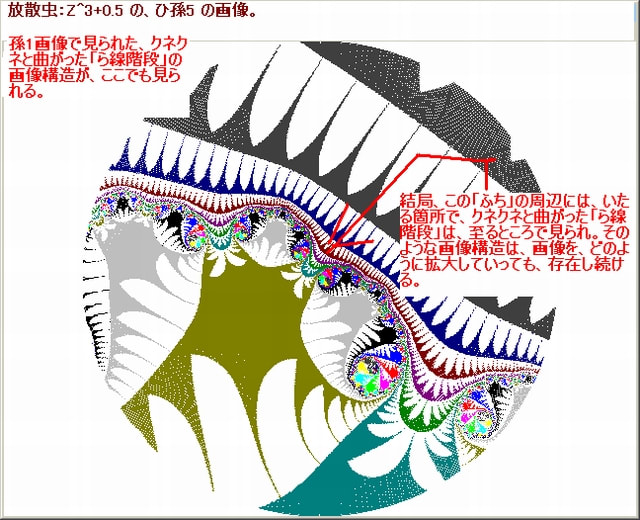
前記事016で、N-loopを脱出するに要するNをNoとしたとき、No=ωとなるような点Zωの存在を示した(但し、あくまでも「ら線階段」図形からの推定だが)。
点Zωは「ら線階段」の収斂点だから、点Zωの数は画像の中の「ら線階段」の数となる。
記事015において、孫1画像の中の4部分を選び其れらの画像を拡大してみた。
其れらの画像の各々には無数の「ら線階段」があった。
(要するに孫1自身のフラクタル画像が無数に存在していた。)
従って無数のZω点が存在していることになる。
其れらの画像・・・即ち孫1の部分画像・・・を見る限りにおいて、無数は無限と言い換えてもよいと思われる(ここに思考の一つの飛躍があるが)。
その無限の大きさ(濃度)を仮にℵaとしよう。
***
さて孫1画像にはZω点はℵa個あることになるが、Z^3+0.5画像は其のフラクタルな画像も無限個ある。なぜなら或る部分(例えば記事014の子1画像のAの部分)の拡大は無限に可能だからである。その無限の大きさ(濃度)を仮にℵbとしよう。
***
さてZ^3+0.5画像の中のZω点の濃度は ℵa*ℵb としてよいだろうか?
ここらへんのことは私は自身はないが、ともかく Z^3+0.5画像のZω点の濃度については私の興味がある。其れは此のZ^3+0.5画像の魅力の一つである。
点Zωは「ら線階段」の収斂点だから、点Zωの数は画像の中の「ら線階段」の数となる。
記事015において、孫1画像の中の4部分を選び其れらの画像を拡大してみた。
其れらの画像の各々には無数の「ら線階段」があった。
(要するに孫1自身のフラクタル画像が無数に存在していた。)
従って無数のZω点が存在していることになる。
其れらの画像・・・即ち孫1の部分画像・・・を見る限りにおいて、無数は無限と言い換えてもよいと思われる(ここに思考の一つの飛躍があるが)。
その無限の大きさ(濃度)を仮にℵaとしよう。
***
さて孫1画像にはZω点はℵa個あることになるが、Z^3+0.5画像は其のフラクタルな画像も無限個ある。なぜなら或る部分(例えば記事014の子1画像のAの部分)の拡大は無限に可能だからである。その無限の大きさ(濃度)を仮にℵbとしよう。
***
さてZ^3+0.5画像の中のZω点の濃度は ℵa*ℵb としてよいだろうか?
ここらへんのことは私は自身はないが、ともかく Z^3+0.5画像のZω点の濃度については私の興味がある。其れは此のZ^3+0.5画像の魅力の一つである。