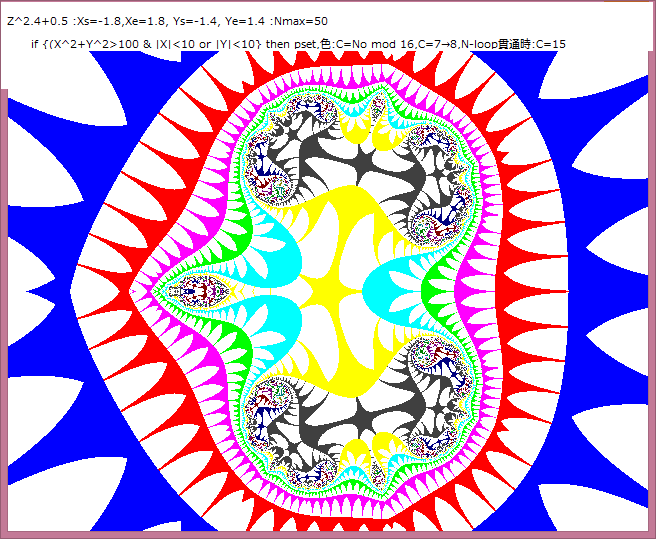
s が正整数ときは、Z^s+C (Cは定数)の画像は、s 個の同じ形状の画像に分割される。(『記事011参照)
では、s が整数でないとき、特に、s=1→2へ変化するとき其の場合のZ^s+Cの画像は、どのように変化していくのだろうか?
そういう疑問のもとに、s を少しずつ変化させたときの、Z^s+C 画像の変化を調べたのが、此の記事である。
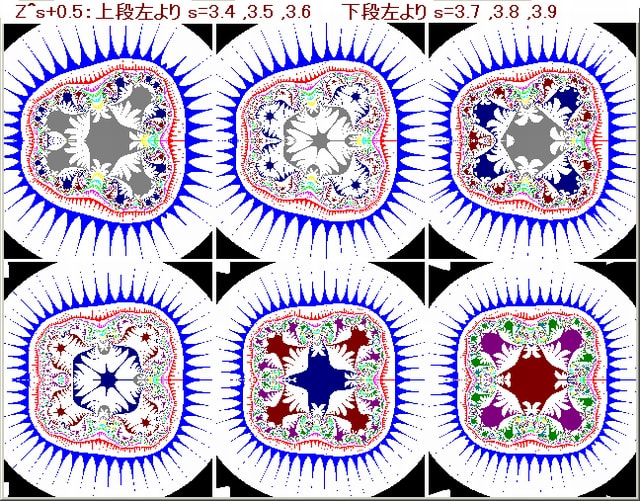
それを調べた結果は下図で示すように或る整数:s の画像から、整数:s+1の画像へ移るとき、整然と s 分割された画像は少しずつ歪みながら分裂していき、整然と s+1 分割された画像に移っていく姿だった。
特に興味深いのは、s =1→2の場合で此れは『何か混沌のようなもの』から始まり、あたかも母体の中の胎児のように『なにものか』へ変わっていく様子だった。
これらの画像に見られる『画像の形態の分裂の様子』は恐らく此の現実の世界の何処かにも実在しているに違いない。
なぜならば此れら画像は、単純とはいえ、決してデタラメなものではなく数学的に厳密な規則のもとで描かれているからだ。
もし我々の周りの現実の世界が数学的な規則に従っていると仮定するならば・・・その仮定の正しさは既に常識だと思われますが・・・これら画像も、幼稚ではあるにせよ此の現実世界の何かの現象への、何かの示唆・暗示であると私は思うからだ。
ガリレオは、『自然の書物は数学という言葉によって書かれている』と言ったそうだ。
だからといって此の世の実在の全てが数学という言語で説明し得る、というわけでは勿論ないだろう。
しかし数学的実在は此の世の実在物(の或る一面への)暗示・示唆であるとは言えるのではないだろうか?
ともあれ『何か予感めいたモノから何かが徐々に胎動し生成していく』
これが以下の画像集の主題である。以下の画像の上に s の変化を書いておく。
また最後の画像の作成条件及びプログラムは最後に書いておく。
----------------------------------------------------------------------











-------------------------------------------------------------------------
また最後の画像の作成条件及びプログラムは以下のとおり。
1.複素関数:Z^s+0.5,s=1, 1.2, 1.4, 1.6, 1.8, 2
2.N-loop脱出条件:X^2+Y^2>100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件:(|X|<10 or |Y|<10) ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
***
BASIC/98での画像作成プログラム。
10 REM Z^S+0.5:6種類表示
40 CHAIN MERGE "C:BASICPROSUBRARCTAN3.BAS",50,ALL
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
140 FOR RR=0 TO 5
150 R1=INT(RR/3)
160 R2=RR-3*R1
170 D1=215*R2
180 D2=242*R1
190 ON RR+1 GOSUB 510,520,530,540,550,560
210 XS=-2 :XE=2 :YS=XS*(238/210)
220 D=(XE-XS)/210
240 FOR J=0 TO 238
250 LOCATE 0,0:PRINT J
260 FOR K=0 TO 210
270 X=XS+D*K
280 Y=YS+D*J
290 FOR N=0 TO 50
300 R=SQR(X^2+Y^2)
310 GOSUB 5000
330 X=(R^S)*COS(S*TH)+0.5
340 Y=(R^S)*SIN(S*TH)
350 Q=X^2+Y^2
360 IF Q>100 THEN 400
370 NEXT N
380 C=15
390 GOTO 430
400 IF ABS(X)<10 OR ABS(Y)<10 THEN 410 ELSE 460
410 C=N MOD 16
420 IF C=7 THEN C=8
430 REM
440 PSET(K+D1,J+D2),C
460 NEXT K
470 NEXT J
480 NEXT RR
490 CLOSE
500 END
510 S=1 :RETURN
520 S=1.2:RETURN
530 S=1.4:RETURN
540 S=1.6 :RETURN
550 S=1.8:RETURN
560 S=2:RETURN