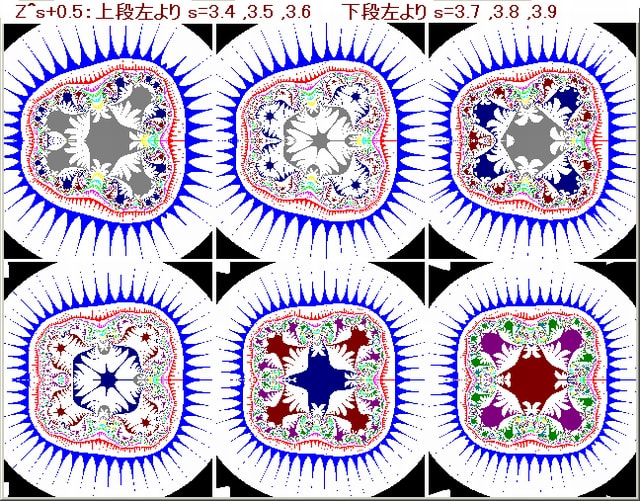
以下の画像作成条件は以下のとおり。
・複素関数:Z^3+C, Cの値は、上段左より0.3,0.42,0.54下段左より0.66 ,0.38, 0.9
・N-loop脱出条件:Q=1/(log|X|log|Y|,(|Q|>10 or |Q|<10)<br />・pset条件:|X|
------------------------------------------------------------

以下の画像作成条件は以下のとおり。
・複素関数:Z^3+C, Cの値は、上段左より0.3,0.42,0.54下段左より0.66 ,0.38, 0.9
・N-loop脱出条件:Q=1/(log|X|log|Y|,(|Q|>10 or |Q|<10)<br />・pset条件:|X|
------------------------------------------------------------








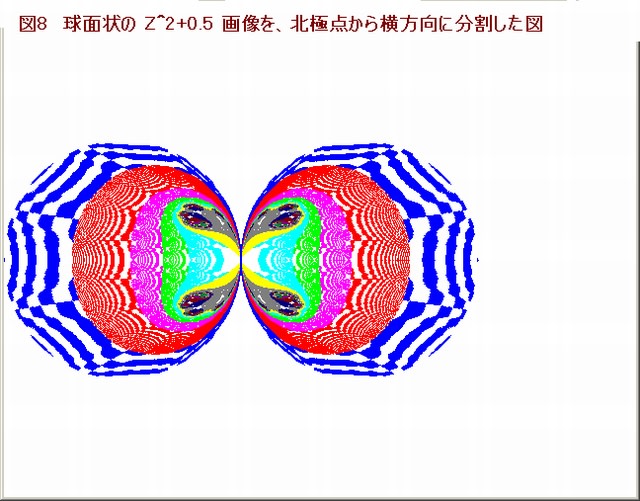

今回取り上げる Z^7+μ画像も其の特徴は本質的に Z^3+0.5画像と同じで、画像の『整然としたフラクタル性』『収束点の数の無限の階層性』等も此の画像を見れば一目瞭然に分かる。
これらの説明は割愛するが、Z^7+μ 画像は、前回記事のZ^5+μ画像同様に画像自体が美しいので掲載する。
なお、この画像作成は以下の手順による。
1.複素関数:Z^7+μ
2.N-loop脱出条件:X^2+Y^2>100 ならば脱出する。Nmax=500
3.N-loop脱出後のpset条件:(|X| N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。
--------------------------------------------
1.図及び2.図は Z^7+μにおいて、μ を変化させた画像である。
1. Z^7+μにおいて、μ を変化させた画像(その1)

2. Z^7+μにおいて、μ を変化させた画像(その2)
3. Z^7+0.365 画像
4. 3.図の 4 箇所の部分を拡大する
5. 4.図の拡大部分を明確にするために背景画像を灰色にする
6. 4.図の1-1の部分の拡大図
7. 4.図の1-2の部分の拡大図
6. 4.図の1-3の部分の拡大図
9. 4.図の1-4の部分の拡大図
------------------
6.図において、超限数在るフラクタル画像が或る特異点へと収束して様子が分かる。
この特異点そのものも超限数個存在している。(記事016,017参照)
9.図において、フラクタル画像が連なっている様子が分かる。その個数は超限個である。
また特異点も超限数個存在している。(記事014参照)

















































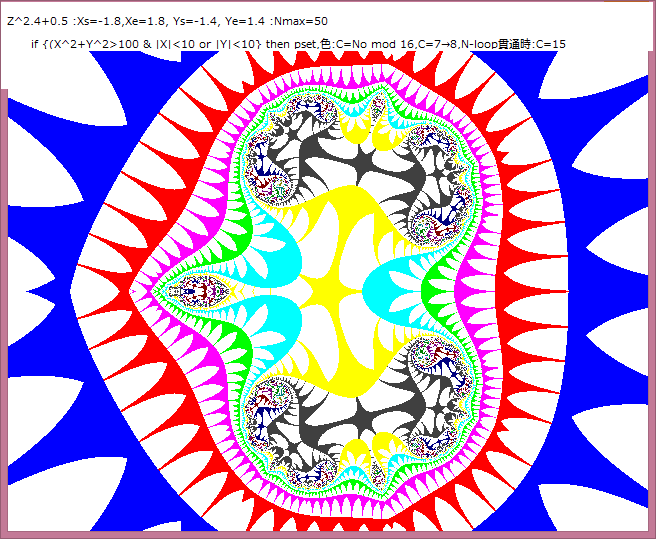



Z^s+0.5,s=2→3 の場合の静止画像は記事029で示した。
その変容は 2 個のモノが 3 個のモノへと変容していった。
この変容を動画にして見たら、どのように見えるだろうか、という興味をもとに
動画を作ってみた。→Z^s+0.5,s=2→3
これは或る種の細胞分裂にも見える。
放散虫:Z^2+0.5 から 放散虫:Z^3+0.5 への「細胞分裂」とでも表現できるだろう。
1という数字は(0を除いて考えると)自然数の最初の値であり、その意味で『ものの始まり』
に対応している。
自然数のその次の数は 2 であるが、1 から 2 へと変化するとき、Z^s+0.5画像は
どのように変化するだろうか。静止画像については前記事029で見た。
そこでは「内臓部」が二つに「分裂」していった。
その変容の様子を動画にしてみたら、どのように見えるだろうか?
そのような興味のもとに動画を作った。→Z^1+0.5→Z^2+0.5
***
この様子は例えれば、此の動画は、1 という何もない原始の混沌の世界から何ものかへと
形が形成していく様子の数学的表現だと言えそうだ。
例えば母親の胎内で胎児が形成されていく様子を連想させる。
この動画は此の世の 『ものの始まり』 とか 『ものがたりの始まり』とかの数学的表現だと私は見ている。