50MHz AM/SSB受信機の復活を目指して その46

「その45」の反省点と改善策
【2017.05.02】
4月28日(金)に投稿した「その45」の内容が、数式だらけの面白みの無い内容となったことについて、暫く考えていた。
記事の内容にクリエイティブ感が全く出ておらず、これでは参考書のカットアンドペーストに過ぎない。
筆者のブログは、教科書でも参考書でも無いが、もっと分かりやすく説明する方法は無いものか・・・
寝ても覚めてもそんな事ばかり考えて約3日が過ぎた今朝、漸く一つの方法を思いついた。
それは、エクセルを使った表計算と散布図による正弦波のグラフ化である。
難解な数式を用いなくても説明できそうである。
エクセルは老若男女を問わず活用されていることは周知の通りで、今回は少々長くなるが、エクセルでの正弦波 (Sinカーブ)の作成方法も含めて紹介して行きたいと思う。
【手順1】
各手順については、手順の下に掲げた写真を参考にして頂きたい。
A列とC列に時間(秒)としての数値を0から1/10000秒単位で0.05秒までオートフィルしながら入力する。
次にE列にB列とD列の合計を表示させるように計算式を入力して、これも0.05秒の行までオートフィルする。
0.05秒までドラッグすると、503行に達する。

【手順2】
B列に下の写真の通り、数式を入力して0.05秒の行までオートフィルする。
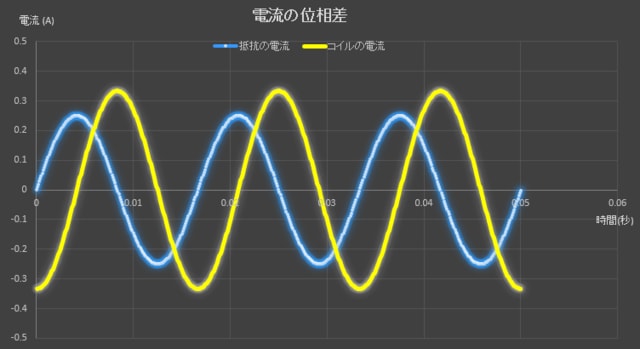
この数式が、「その45」で言うところの抵抗に流れる電流の正弦波(Sinカーブ)の関数になる。
この数式は公式そのものだが、最初についている「0.25」は正弦波の半サイクルのピーク電流値を意味する。

【手順3】
D列に下の写真の通り数式を入力して0.05秒の行までオートフィルする。
この列に表示される数値が、「その45」で言うところのコイルに流れる電流の「各時刻における瞬時値」である。
関数の最初についている0.3335は正弦波の半サイクル（周期）のピーク電流値を意味する。
又、後ろ側についている-0.5×3.14は位相が90°遅れていることを意味する。

【手順4】
手順1～手順3を行うと、E列に「各時刻における抵抗とコイルの合成電流」の計算結果が表示される。
例えば、回路が動作を開始して0.001秒後の瞬間的な合成電流（瞬時値）は-0.21802A(アンペア)だと分かる。
マイナスと表示されるのは、有る方向をプラスと仮定した場合に逆方向に向かって流れていると言う意味である。

【手順5】
503行目まで達した表計算の様子は、下の写真の通り。

【手順7】
散布図を作成する為に、A列～D列に表示された全ての数値を選択する。

【手順8】
エクセルの「挿入タブ」のグラフ機能から「散布図」を選択する。
グラフタイトルや表示色等の変更方法については、省略する。

【手順9】
E列の数値をくくると、その中の最大値が一番下のバーに表示される。
ここでは、0.416958764A(アンペア)と言う事になり、これが半サイクル(周期)の値なので1周期では2倍の0.83Aと言う事になる。
この値が、抵抗とコイルの合成電流の最大値で「その45」での平方根を使った計算式の結果と一致する。

冒頭のグラフを、再度見て頂きたい。
これが僅か0.05秒と言う短時間の中で起こっている事象である。
0.05秒以降も同じ動作を繰り返す。

其々の波形の変化の様子は「位相」と呼ばれる時間的なズレが有る為、各時刻における合成電流は、単純にピーク値を足すと言う訳には行かないのである。
ところが、関数で導き出された各時刻の瞬間的な数値であれば、上述の通り「単純な足し算」で計算が成り立つ。
一言で「単純な足し算」と言っても、これだけ面倒くさい話になってしまうのだから電気回路を理解するのは簡単では無い訳だ。
今日(5月2日)は記事投稿の為、早朝から資料の作成に入り,記事が完成したのは14：00を過ぎており、結構疲れたが達成感を得る事ができた。
以上、ＧＷの8連休の中のほんの1ページであった。


本稿続く・・・