数学的実在とは－幾何学－3－原論と基礎論(1)

　先日の続きです。

　例えば、ヒルベルトの公理系の最初には「結合の公理」が登場します。点と直線だけに関していて平面には関与していないものを挙げます(*1)。
　　１．２点と結合する直線がつねにただひとつある
　　２．１直線と結合する点がつねに少なくとも２つある。
　　３．１直線と結合しない少なくとも３点が存在する

　ここで"結合する"とした用語はわかりやすくすれば、公理１でなら「２点を結ぶ」、２と３でなら「１直線上に」とするところです。それをわざわざ同じ言葉にしたのは、双対性(duality)というものを示しやすくしたかったからです。双対性とは命題の中の２つの用語を交換した命題もまた成立するという性質で、ある公理系が持つ性質ということになります。平面幾何学の場合は、点と直線を交換した命題が成立するかどうかということです。結合の公理の双対命題は次のようになります。
　　１d．２直線と結合する点がつねにただひとつある
　　２d．１点と結合する直線がつねに少なくとも２つある。
　　３d．１点と結合しない少なくとも３直線が存在する

　多くの幾何学モデルでは２dと３dは成立します。しかし、１dはユークリッド幾何学では成立しません。成立するのは次の定理で、これは背理法により、公理１を使って証明できます。
　　１e．２直線と結合する点は１個または０個である

　すなわち、１eの否定は「２直線と結合する点は２個以上」ということですが、これは公理１の「ただひとつ」という条件に矛盾するのです。

　厳密には、ユークリッド幾何学ではさらに次の命題も成立しています。"または"を安易に解釈すると１eは１eeも含んでいると勘違いしかねません。
　　１ee．２直線と結合する点が０個の場合がある。
　　　(１直線と交わらない直線が存在する)

　１eeはつまり平行線が存在すると言っているわけです。１dを満たす"モデル"は１eeを満たしていなくても１eは満たしますから、１dを満たす"モデル"は結合の公理３つを満たしています。このようなモデル、すなわち平行線が存在しないモデルには例えば球面や射影平面があります(01/15記事)。また３点と３直線からなる図1Aのモデル(３点３線モデルと命名します)も結合の公理３つとその双対公理３つを満たしています。３点３線モデルは普通の幾何学的空間とは非常に違って見えますが、点が無限にあるなどという定理や公理はまだ出てきていませんからこれでもモデルになるのです。

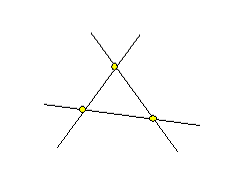
　　図1A

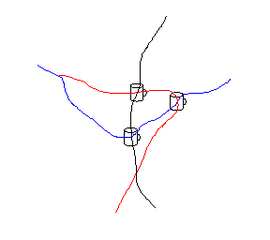
　　図1B

　さて射影平面や３点３線モデルでは、１～３、１d～３dが成り立ち、双対性が成り立ちます。なので、定理中の点と直線を入れ替えても体系としては正しいものになり、両者は全く対等です。形式主義から言えば、両者は区別ができません。でも我々が３点３線モデルを眺めれば、明らかに点と直線は別物として認識されます。これは、１～３、１d～３の公理だけでは、我々が直観的に認識している３点３線モデルの性質のいくつかが表現されていないということを意味します。

　また、１～３、１d～３dが成り立ち３つの点と３つの直線から成る系だけならば、図1Bのようにぐにゃぐにゃの曲線を"直線"と見なしてもかまいません。しかし我々の直観では、図1Aと図1Bには違いがあります。このように直観的に区別できる性質を証明するためには、結合の公理に加えて色々な公理を導入する必要があるのです。

　　　続く

－－－－－－－
*1) 原著(ref4;01/01記事)では次の３つの公理。本稿ではⅠ1とⅠ2をひとつにまとめ、Ⅰ3を２つに分けた。
Ⅰ1.二点Ａ,Ｂに対し,これらの二点のおのおのと結合する少くとも一つの直線がつねに存在する。
Ⅰ2.二点Ａ,Ｂに対し,これらの二点のおのおのと結合する直線は一つより多くは存在しない。
Ⅰ3.一直線上にはつねに少くとも二点が存在する。一直線上にない少くとも三点が存在する。