こんな問題ですが？？？？？認知症予防には、？？？？？？
小学校？中学校？
いつ教わった？？？？？？
(意見には個人差がありました。）
二つの問題に挑戦しました。
なお、本来は、円の面積は、π×直径^2÷4ですが、この問題に関しては、π÷4は省略します。
計算テクニック上、無意味なので、省略してもまったく影響はありません。
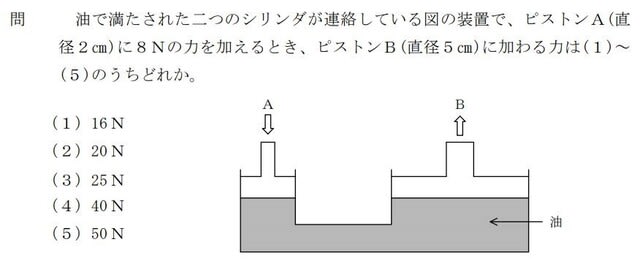
PA÷A＝PB÷B、AはピストンAの断面積、BはピストンBの断面積です。PA＝8Nです。
求める問題は、PBですから、PB＝PA×B÷Aです。
PB＝8N×5^2÷2^2＝8N×25÷4＝50N となりそうです？
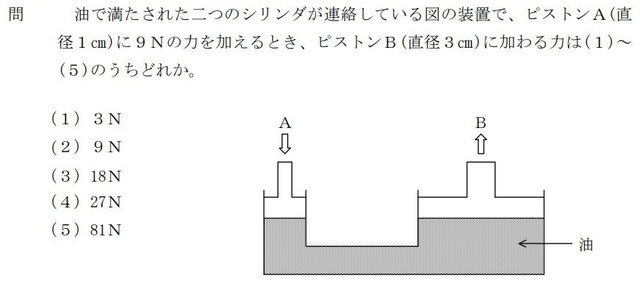
PA÷A＝PB÷B、AはピストンAの断面積、BはピストンBの断面積です。PA＝9Nです。
求める問題は、PBですから、PB＝PA×B÷Aです。
PB＝9N×3^2÷1^2＝9N×9÷1＝81N となりそうです？
もし、間違っていたら・・・・・・・認知症かも？？？？
(意見には個人差がありました。）
流石、僻地の自治体だ😅
久しぶりに目にした言葉だ😅
『フロッピーディスク💾』
20代、見たこと無いよね😅
デジタル化、進まない訳だよ😁
98💻❔❔❔❔❔
まさかぁ～😒
骨董品マニアに売れる❔❔❔❔❔無理😨😨😨😨😨
しかし、まぁ～😄😄😄😄😄😄😄
『フロッピーディスク💾』ねぇ～😒
平和だ😅この国は平和だ😅
使ってるんだぁ～😒
凄い❗
意見、見解、解釈、受け止め方、その他、個人差が有りました🙆😊😄💕🏡💑❗
これって、同じ問題ですが、別な試験なんですよ？？？？？
つまり、同じような傾向があるので、若干、数値を変えたりして、使い回ししてるんです。
だから、必ず、出題されるものとして、しっかり、「記憶」しましょうね。
解法を正しく、理解しましょうね！
▲の支点に対して、Bの60kgは、「反時計回り」、必要な力Pは、「時計回り」に、回転します。
バランスがとれていれば、この「てこ」は、水平状態です。
それぞれの支点との距離によって、バランスするので、
図中に示す計算をすれば、正解が得られます。
重要なのは、支点との距離を誤らないことです。支点～Bは、0.5ｍ、支点～Ａは、2ｍ・・・・そこがこの問題の「ポイント」ですよね。
勿論、ｋｇとＮとの単位換算も重要ですが・・・・・・・・ＳＩ単位で育った世代には、問題ないでしょう！
(意見には個人差がありました。）
ある国家試験の問題に、引張応力を計算する問題が有りました。
学生時代、「材料力学」を勉強したとき、概ね一丁目一番地とも言える計算問題です。
挑戦しました。
仮に、正確に計算したとして、σ＝12.48N/m㎡です。
小生の「ざっくり計算」では、13.3N/m㎡でした。
選択肢は、12か？25か？31、50、62は、明らかに違います。
小生のざっくり計算は、結果が大きめに求まることは明らかですから、誤差が大きくても、20とか？22とかではありません。
どちらかと言うと、13とか？17とか？小さい方に振れますから・・・・・・・「最も近いもの」を選ぶとしたら、（１）でしょうね？
もし、間違っていたら・・・・・それは、「認知症」かも？
正確さは重要ではありません。どの程度の数値なのか？
それは、１０なのか？50なのか？100なのか？
11.1や、11.3や、12.2や、ちまちました正確さは必要ありません。そこが重要なのです。
(意見には個人差がありました。）
今日は、クレーン登載車に関連する死亡事故が発生しました。
操作で大事なのは・・・・・「バランス」です。力学的なバランスです。重心です。
そこで、「クレーン」関係の「公表問題」に、こんな問題がありました。
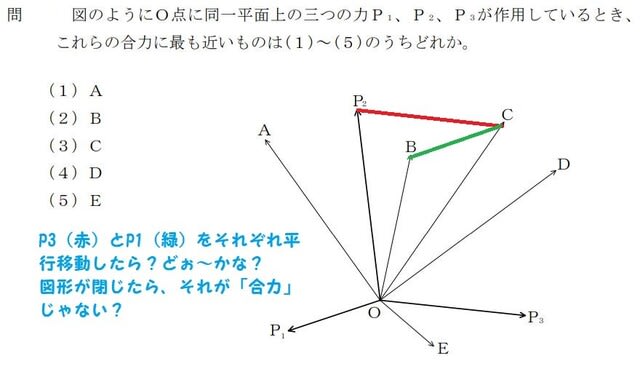
最近、これと同様の問題を解いて、ブログに掲載しましたが・・・・それは、「林業」関係です。
どんな職種でも、「バランス」は重要なのです。
どんな職種でも、「物体の重心」は重要なのです。
(意見には個人差がありました。）
新しい計算問題に挑戦しました。
なお、本問題を解くために、「わかり易い設備工学講座③衛生設備」（彰国社）を参照しました。
(意見には個人差がありました。）
