メモ2

　タクシー数(その8)、(その９)で実2次体の整数の5乗数の和で2通りに表される例を多数見た。

そのためには、

 

を満たす解(k,δ,b)のうちδ≠0かつ、t,t’>0となる解を求めればよかった。ここで

 

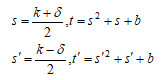
である。この時、t,t'が有理数の平方であれば、整数の5乗数の和で2通りに表される例が求められるこ

とになる。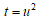　　とおけば　　である。これを最初の式に代入すると、

 

これを展開して整理すると、

 　

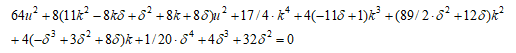
したがって、この式の解で(u,k,δ)でδ≠0なる解を求めればよい。

δ=0となる解としては、以下がある。

 　ｊは有理数

 

 

　　として元の方程式に代入しjとδの方程式としδで割ると，　

 

これを満たす解があれば、整数の5乗数の和で2通りに表される例が求められるということになるかな。