
違いは何なの?
学校で教わる方法と highdy の提唱する方法の違いは、何処にあるのでしょう。
一般的に多い2桁や3桁の暗算においては、一桁の掛け算を多数繰り返しながら、足し算を併行して最終的な答えを求めます。
その過程で、足し算の回数を減らそうと考えたのが highdy の方法で、瞬間的な記憶の苦手な方には不向きな方法かも知れません。
しかし、脳を良く使う過程にある時期(小学校~大学時代)に訓練すると、とても効果のあるものです。老年者になってくると、記憶が段々苦手になって来るものです。
具体的にその違いを比較してみましょう。
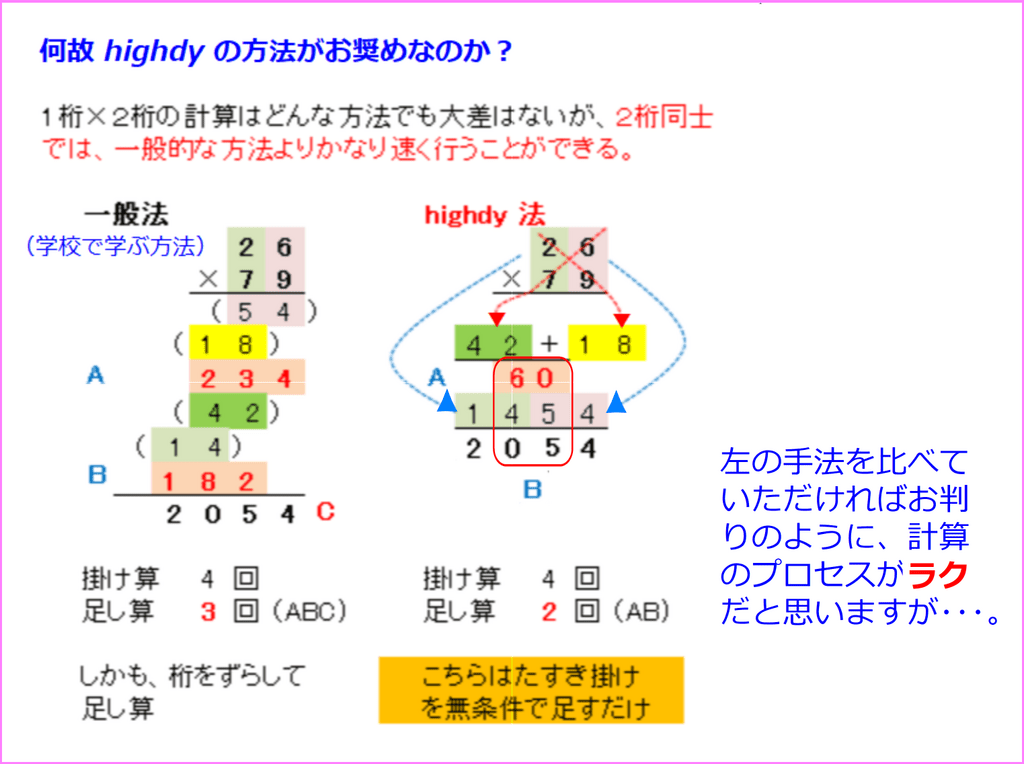
3桁の計算では?
2組の数字の掛け算で、一方が3桁の場合はどうでしょう。
基本的に考え方は、無条件に1桁の掛け算をする最上位、最下位の計算はそのままで、その中間部に加える数字を算出するための加算部が2桁同士の足し算ではなく、一方が3桁になる点が異なります。
多数練習して十分に慣れないと、うっかり「0」を落として桁違いのミスを犯してしまいます。

人は悪い習慣を改めるのに時間がかかるように、慣れた行動に対して新しい行動を身につけるにはかなりの努力が必要です。
でも、努力する人は他人に差をつけることができるのも事実で、それが宇宙の真理とも言えるもので、努力に対するご褒美でその分ラクができます。
でも、努力する人は他人に差をつけることができるのも事実で、それが宇宙の真理とも言えるもので、努力に対するご褒美でその分ラクができます。
オマケのひと言
昨日、2泊3日の信州旅行から帰って参りました。
昨日、2泊3日の信州旅行から帰って参りました。
とても楽しく、ため(勉強:また知識が増えた?)になった旅でもあります。ずっと標高の高い所に滞在し、下界(?)に降りてくると、大変な暑さを感じます。
美味しいものの食べ過ぎで、暫くは体重計には乗らない方が精神的にいいのではないかと考えています。旅行中運動(と言ってもウオーキングのみ)も良くしましたが、それ以上に栄養分を摂っているような気がします。
素敵なデュエットのフルートまたはオカリナのミニコンサートもあり、至福のひと時でした。(そのうち機会を見てご報告します。)
素敵なデュエットのフルートまたはオカリナのミニコンサートもあり、至福のひと時でした。(そのうち機会を見てご報告します。)
このシリーズは10回以上続きます。
どれか一つ覚えておくだけでとても役に立ちます。
本日もご来訪いただきありがとうございました。


















2桁なら全く問題なくできると思います。
考え方は同じですが3桁になるとたすき掛けの部分で桁数が変わってきますので、暗算して加算する数字を間違いやすくなります。
数字を上下に並べてのたすき掛けを、横に並べて考えるといいかも知れません。
まだ、インド式の研究はしていませんが、ひょっとするといいアイディアがあるかも知れません。この手の研究には時間がかかります。数学者ならもっと素晴らしいことを考えられるかも知れませんが、他に便利な方法があれば、もうとっくに発表されている筈ですよね。
このシリーズ(7)で思わぬ感動を覚え、何度も何度もやってほぼ会得しましたので今回も今、メモ用紙をたくさん用意し、あれやこれやとやっているのですが・・・
例題の7や8のたすき掛けが思ったより難しく感じました。
3桁になると2桁の計算ではなく1桁上がる・・・というところの理解が咄嗟にできませんでしたので。