
(予約投稿) ただいま信州を旅行中!
究極の掛け算?
以下の計算法は究極の暗算法? とにかく素晴らしい発想で、これぞ究極の暗算法と思いきや、掛ける数字のいずれもが10位が9であることが条件です。
以下の計算法は究極の暗算法? とにかく素晴らしい発想で、これぞ究極の暗算法と思いきや、掛ける数字のいずれもが10位が9であることが条件です。
しかし、覚えておいて損をするものではなく、知識は多いほど良いものです。
ちなみにこの方法は highdy が考えたものではありません!
ちなみにこの方法は highdy が考えたものではありません!
それぞれ100から掛ける数字を引いて、出た答え同士を足して100から引いた値と、出た答え同士を掛けた値を並べるだけ。
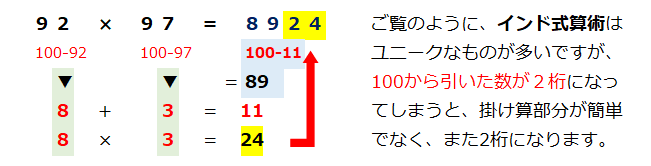
10位の数字が8以下の場合では、同じ方法では上手くいきません。
最も一般的な計算プロセス
学校で教わる方法と highdy の提唱する方法の違いは次回解説しますが、highdy の2桁の掛け算の一般的な手法を先にご紹介します。
これまでの様々な暗算法がどうしても覚えられない人(そんな方は滅多におられないと思いますが・・・)は、以下の方法を試みてください。
図式解法と比べれば、正しい計算であることがご理解できると思います。
ただ、どんな方法であれ、新しいことは数多く練習しないと覚えられないものです。
最も一般的な計算プロセス
学校で教わる方法と highdy の提唱する方法の違いは次回解説しますが、highdy の2桁の掛け算の一般的な手法を先にご紹介します。
これまでの様々な暗算法がどうしても覚えられない人(そんな方は滅多におられないと思いますが・・・)は、以下の方法を試みてください。
図式解法と比べれば、正しい計算であることがご理解できると思います。
ただ、どんな方法であれ、新しいことは数多く練習しないと覚えられないものです。
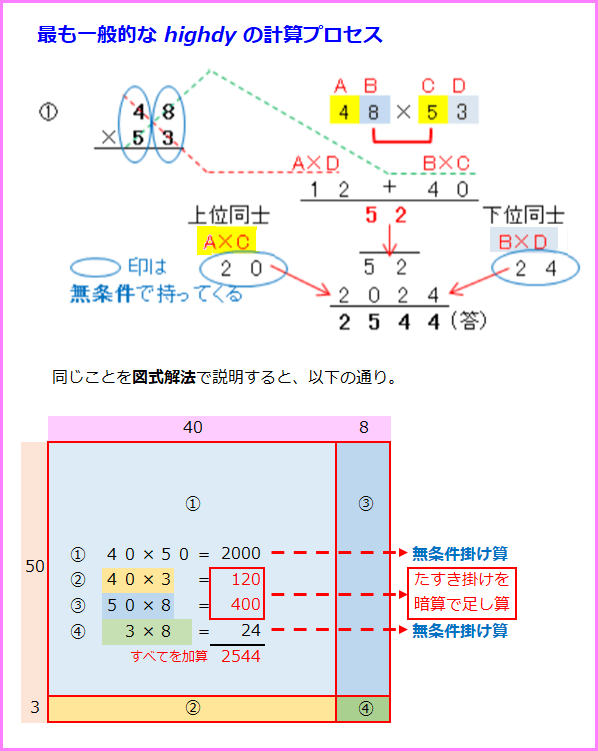
暗算で求めた52(実際には520なので)を足す位置(位)を間違えないことです。
2桁の掛け算であれば、1000と100の位、10と1の位はそれぞれ最大81(=9×9)で繰り越しが無いため、無条件に掛けた数字を表記しても使える方法なのです。
オマケのお話
ホームページを開設した2008年頃だと思いますが、highdy が高校時代に思いついたものを一部手を加えて「新天才教育法」として発表しました。
その数年後位に「インド式算術」が爆発的に流行したこともありました。
ちょうど安倍政権の腐敗政治の露呈と、誤ったゆとり教育、衰退途上国化が始まった途端に人気も下火になって意外に普及しなかったようです。
いまでも、続けて教えている塾もあるようです。
highdy はボランティアはしても、働く(金儲けをする?)気は全く無いので、この方法も闇に葬られる(?)かも知れませんが、こんなことを考えている棺桶に片足を突っ込んだ後期高齢者もいたということで・・・。
highdy はボランティアはしても、働く(金儲けをする?)気は全く無いので、この方法も闇に葬られる(?)かも知れませんが、こんなことを考えている棺桶に片足を突っ込んだ後期高齢者もいたということで・・・。
このシリーズは10回以上続きます。
どれか一つ覚えておくだけでとても役に立ちます。
本日もご来訪いただきありがとうございました。


















おたかさんのdandy-hidechan52です
今回、連載中の計算を始めてランダムな2桁同士で計算して、電卓で確かめたところ
合っていたので、間違いなく覚えられたようです
面白い計算方法ですね
何種類もの数字で例を作り、確かめたのですがこの計算方法が私には一番わかりやすく
すぐに理解でき、かつ使えました。
中学・高校の頃、何の役に立つのだろうと思っていた因数分解の公式も、先生がこのような利用法を教えていたらもっと興味が湧いたかも知れません。
文部科学省の固い頭の方々の影響もあるかも知れませんが、どうも学校の先生は教え方が上手くない方が多いように思います。
教育というものは楽しくないと、勉強意欲が湧かないものです。
いつもチャレンジ精神が旺盛な fumiel-shima に驚きます。やはり、そのお気持ちが若さを保つ秘訣かも知れません。
歳を重ねて新しいものに挑戦しなくなると、殆どの方が老い始めます。常に新しいことなど、何かクリエイティブなことやスポーツを続けている限り、精神的にも体力的にも若さを維持することができます。
私も今回の旅行でまたまた新しいテーマを見つけました。いつまで経ってもやりたいことが多くて、時間が足りません!!