今回の画像は、複素関数:Z^Z+Z^s+C ,(C=0.3) において、s=1→24 変化させたときの画像の変容である。
先ず、s=1→6 の場合の変容が下図である。

次に、s=7→24 の場合の変容が下図である。下図は上図の 2 倍に拡大している。s が 7 以上では 変容は、ほとんど変化していないことが分かる。



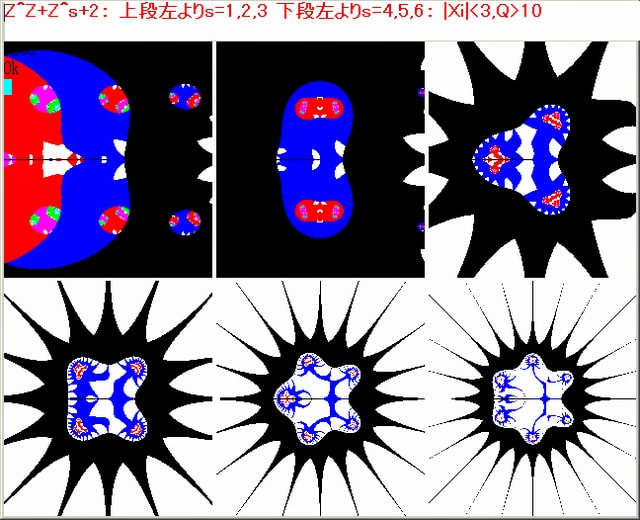
次に、複素関数の C を、0.3→2 に変えて、上と同様に、s=1→24 まで変えてみる。先ず、s=1→6 の場合の変容が下図である。
次に、s=7→12 の場合の変容が下図である。下図は上図の 2 倍に拡大している。

上図では“内臓”部が表示されていない。表示できるように、N-loop脱出条件『もし、Q=X^2+Y^2>Tならば脱する』のTを、T=10→5 に変更した。
その変更条件での、s=7→24 の場合の変容が下図である。
下図において、青い変な“虫”が入った目玉模様の図が、ちょうど、s 個、円状に並んでいることが分かる。



以上の画像より、複素関数:Z^Z+Z^s+C の、s の変化による変容は、C が小さいとき(例:C=0.3)は、Z^s 項は、あまり寄与せず、C 大きいとき(例:C=2)は寄与している、ということが分かる。
先ず、s=1→6 の場合の変容が下図である。

次に、s=7→24 の場合の変容が下図である。下図は上図の 2 倍に拡大している。s が 7 以上では 変容は、ほとんど変化していないことが分かる。



次に、複素関数の C を、0.3→2 に変えて、上と同様に、s=1→24 まで変えてみる。先ず、s=1→6 の場合の変容が下図である。

次に、s=7→12 の場合の変容が下図である。下図は上図の 2 倍に拡大している。

上図では“内臓”部が表示されていない。表示できるように、N-loop脱出条件『もし、Q=X^2+Y^2>Tならば脱する』のTを、T=10→5 に変更した。
その変更条件での、s=7→24 の場合の変容が下図である。
下図において、青い変な“虫”が入った目玉模様の図が、ちょうど、s 個、円状に並んでいることが分かる。



以上の画像より、複素関数:Z^Z+Z^s+C の、s の変化による変容は、C が小さいとき(例:C=0.3)は、Z^s 項は、あまり寄与せず、C 大きいとき(例:C=2)は寄与している、ということが分かる。









