下図は以下の画像である。
・複素関数は、Z^f(Z) で、f(Z) は、前記事同様、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。
・N-loop脱出条件は、『Q=1/(log|X|log|Y|)として、もし、(|Q|>10 or |Q|<0.1 ならば脱出する』。
・pset条件は、『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならば、psetする』。
下図は、上記条件の 6 種類の関数の画像の一括表示したもので、下図の上段左より、f(Z)= sin Z , cosh Z, e^Z 。下段左より、f(Z)=Z^2, Z^3, Z^4。

次に、6 種類の関数の画像を個別に紹介します。
sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。
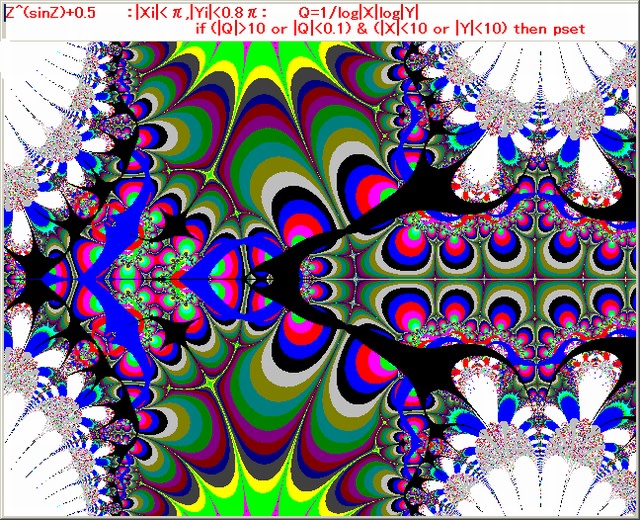





・複素関数は、Z^f(Z) で、f(Z) は、前記事同様、sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の 6 種類。
・N-loop脱出条件は、『Q=1/(log|X|log|Y|)として、もし、(|Q|>10 or |Q|<0.1 ならば脱出する』。
・pset条件は、『N-loop脱出後、もし、(|X|<10 or |Y|<10)ならば、psetする』。
下図は、上記条件の 6 種類の関数の画像の一括表示したもので、下図の上段左より、f(Z)= sin Z , cosh Z, e^Z 。下段左より、f(Z)=Z^2, Z^3, Z^4。

次に、6 種類の関数の画像を個別に紹介します。
sin Z , cosh Z, e^Z, Z^2, Z^3, Z^4 の順に示す。






















