朝の日課・・・
先日ボランティア活動できれいにしていただいた。
( 2020/11/19 夏日 ボランティア活動ご苦労様です )
何年かぶりに歩くことができた。
ありがとうございました。
You Tubeを見ていると面白い動画が投稿されている。
そのひとつ、「鈴木貫太郎さん」の動画で
簡単な詰将棋。
短い詰手数は日に3問。
ていねいに、面白く解説してくださる。
以前私は趣味として簡単な詰将棋を繰り返し解いていた。
そのせいか、この問題は1秒以内で解けた。
シャツの数式で分かるように数学もお得意。
入試問題も投稿されている。
解けそうな問題があると、ついつい解きたくなる。
分子の 3007 の約数はすぐには思いつかない。
分母 3201 の約数は 3で割り切れ、
( 2013/07/24 2で割り切れる数、3で、4で、5で・・・ )
また、( a + c ) ー ( b + d ) = 0 であることから
11で割り切れる。( 2015/01/12 11で割り切れる数 )
その結果
3201 = 3 × 11 × 97
問題の意図から分子 3007は 97で割り切れるだろう。
97で割ると
3007 = 31 × 97
したがって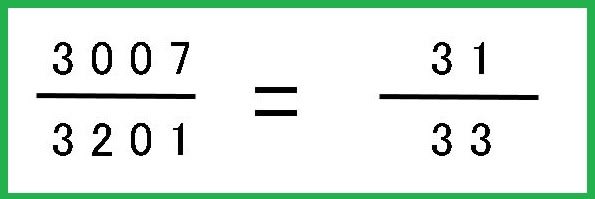
となる。
もう1問。
力ずくで
11 × 11 × 11 + 397 = 1728
これを
2で割り、2で割り・・・ 、3で割り・・・
となる。
問題の意図するところは 11の3乗のあることから
3乗の公式を求めているかもしれない。
公式にあてはめようとすると、かえってややこしくなる。
2問とも高校入試問題。
晴















