ある組織-2-その規則

前回から続く

　さてこれまで適当な員のクラス{a,b,・・・}があると、その上司がいるものとして来ましたが、クラスによっては上司がいないかも知れません。そもそもクラスに属する員の数がどれほど多いかが不明なのです。単に無限大というだけではなく、実数よりも濃度の大きいとてつもない無限大の員の数も考えられるのです。

　そこで「員の集まりの上司」を任命するための明確な規則が定められています。

規則２．員aと員bだけを部下とするを上司を員として任命できる

　つまり２人の員がいれば新しい上司が任命できるわけです。特別な場合として員aと員bが同一人物の場合は、一人の員だけを部下とする上司が任命できます。φのみを部下とする員１を任命したのは、実はこの規則を使ったのです。ここで、上司に任命された人物はどこから来たのだと思うかも知れませんが、それはどこかからxをスカウトしてきて組織Ｖの成員としたのだと思って下さい。人材の供給源は無尽蔵です(^_^)。
　ということで、規則２も論理式で表しておきましょう。

規則２．∃x∀y(y∈x⇔(y＝a∨y＝b))

　つまり、「員yが員xの部下であることと、員yが員aまたは員bであることとが同値である」というわけで、そんな員xが存在するよ(任命できるよ)と定めているのです。

　次に紹介する規則３は、少し複雑ですが図２もご覧下さい。

　員aの部下をz1,z2,・・・とします。・・・の部分は自然数以上の濃度かも知れません。このz1,z2,・・・のそれぞれの部下を全て集めたクラスを考え、このクラス員だけを部下とする員が任命できる。というのが規則３になります。正確を期すために論理式で示すと

規則３．　∃x∀y(y∈x⇔(∃z∈a(y∈z)))
別の表現　∃x∀y(y∈x⇔(∃z(z∈a∧y∈z))


　　　　　　　　図２

　zが員aの部下、yが員z＝z1,z2,・・・の部下、xが新たに任命された上司です。結局の所はz1の部下全員,z2の部下全員,・・・を全て合わせた全員だけを部下とする上司xが新たに任命されるのですが、ここでなぜz達が特定の員aの部下であるという制限をつけるのでしょうか？　それは言ってみれば、新たに任命する上司の部下は身元のはっきりした員のみにしたいからです。逆に言うと、すでに上司のいる員は身元がはっきりしている員ばかりということになります。身元がはっきりしているというのは、組織Ｖの成員であることが明らかである、と言い換えてもよいでしょう。

　例えば員aが３(∋{φ,１,２})とすると、
　　　z＝φ、１(∋{φ})、２(∋{φ,１})
　なので、
　　　y＝φ,１
　であり、つまり　x＝２(∋{φ,１})　です。

　員aが４(∋{φ,１,２,３})とすると、
　　　z＝φ、１(∋{φ})、２(∋{φ,１})、３(∋{φ,１,２})
　なので、
　　　y＝φ,１,２
　であり、つまり　x＝３(∋{φ,１,２})　です。

　一般に員aがｎ(自然数)とするとx＝ｎ－１です。


　さて図２でわかる通り、規則３では任命済みの員aよりも下のランクの上司しか任命できません。規則２なら任命済みの員aと員bより１つ上のランクの上司を任命できますが、それは２人の員だけを部下とする上司です。では３人以上の場合はどうなるのでしょうか？　これは図３のように、規則２と規則３を組み合わせることで可能になります。


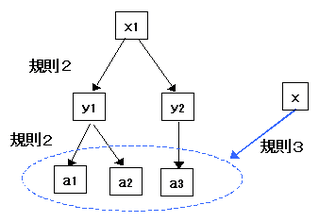
　　　　　　　　図３

　すなわち員a1,a2,a3がいるとき、a1とa2だけを部下とする上司y1を任命できます(規則２)。またa3だけを部下とする上司y2を任命できます(規則２)。すると、y1とy2だけを部下とする上司x1を任命できます。ここで規則３を使うと、a1,a2,a3だけを部下とする上司xを任命できます。

続く