ある秘密めいた組織Vがあり、その構成員(以下、員と略します)の間には「直属の上下関係」というものがあります。員aの直属の上司が員bであることを、「a∈b」と書き表すことにします。これは、員aは員bの直属の部下であるとも言えます。直属でない間接的な上下関係というものは定められていませんので、以後、上司とか部下とか言えば、直属であると考えて下さい。員aの部下の部下は員aの部下ではないのです。
一人の員が直属の部下を何人持っても構いません。また、人間の多くの組織とは異なり、一人の員が直属の上司を何人持っても構いません。ただし、ある員の集まりがあるとして、その集まりの全員だけを部下に持つ上司というのが、もし居るとすればそれは唯一人しか許されない、という規則があります。言い換えると、もし員aと員bの持つ部下が全員同じであるとすれば、実は員aと員bは同一人物であるということです。これはまた、ある員の部下を全員特定すれば、その員が唯一人に特定できるということでもあります。これを正確に示すために論理記号で表せば次のようになります。
規則1. ∀x(x∈a⇔x∈b)→a=b
「その集まりの全員だけを部下に持つ上司」では長いので、簡単に「員の集まりの上司」と呼ぶことにします。もちろん直属の上司です。
この規則1のもとでは一見、員の集まりと員とが1対1に対応するように見えますが、そうではありません。まず、一人も部下のいない員がいるかも知れません。また員の集まりで、「その集まりの上司」がいない場合もあり得ます。「員の集まり自体」と「その集まりの上司」を混同しては拙いので、「員の集まり自体」はクラスと呼ぶことにします。特に「その集まりの上司」がいないクラスだけをクラスと呼ぶ場合もあります。
ではこの組織には具体的にどんな員がいるのか。
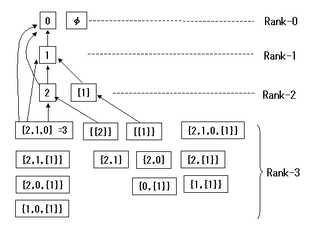
図1
一人も部下のいない員がいるかも知れないと書きましたが、実はそのような員が唯一人だけいて、φ(ファイ)という名を持っています。別名ゼロ(0)とも呼ばれます。ミスターゼロとはなかなか良い名前です。
員φだけを部下とする員もいて1(イチ)と呼ばれています。員φと員1だけを部下とする員もいて2と呼ばれています。員φと員1と員2だけを部下とする員もいて3と呼ばれています。以下同様に続き、どんな自然数nについても、員φと員1と・・・員nだけを部下とする員もいて(n+1)と呼ばれています。つまり自然数に対応するだけの無数の員がいることが判明しました。今紹介した員達はゼロから始まる自然数全てと1対1に対応しますので簡単に「自然数員」と呼ぶことにします。
さて驚くべきことに、これら無数の「自然数員」の全員だけを部下とする員もいるのです。この員は普通ω(オメガ)と呼ばれています。さらに、ωとφだけを部下とする員もいて(ω+1)と呼ばれています。と、またまた続くのですが、その前に。
例えば員4の部下は{φ,1,2,3}の4名です。この4名の中の何名かで作る集まり(クラス)は次の通りです。
{φ,1,2,3}
{φ,1,2}、{φ,1,3}、{φ,2,3}、{1,2,3}
{φ,1}、{φ,2}、{φ,3}、{1,2}、{1,3}、{2,3}
{φ}、{1}、{2}、{3}
これらの15個のクラスにも全て上司がいますが、その15人の中にはすでに出てきた員もいます。つまり、クラス{φ,1,2,3}、{φ,1,2}、{φ,1}、{φ}の上司はそれぞれ4,3,2,1です。また、この中で員3を含まない7個のクラスは実は員3の部下である{φ,1,2}の3名で作られるクラスでもあります。員3を含むクラスの上司はいわば員4と同格と言えて、「ランクが4である」と呼ばれます。
上の作り方でのランクnの員の数は(2^n-2^(n-1))となることはわかりやすいでしょう。しかし、ランクnの員はこれだけではありません。つまり下から挙げてゆくと、
ランク0 φ
ランク1 1(∋{φ})
ランク2 2(∋{φ,1})、{1}
ここで{1}、つまり員1だけを部下とする員が登場しました。この員をS{1}と名づけるとすると、ランク3の員は{φ,1,2,S{1}}の4名の中の何名かで作るクラスの上司で、ランク2以下ではない員です。
むしろランク3以下の員の数は2^4という方がわかりやすいでしょう。
一般にはランクn以下の員の数をS(n)とすれば、
S(n)=2^(S(n-1))
です。結局S(n)は次のように累乗を重ねた数になります。この表現はタワーと呼ばれます。
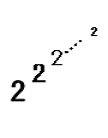
ちなみに、Tower(1)=2、としてTower(n)の値を列挙すると、
Tower(2) = 4
Tower(3) = 16
Tower(4) = 216 = 64*1024
Tower(5) = 265536≒64*10(6553*3)
逆に言うとタワーという表現は、これほどの巨大な数を実にコンパクトに表現できるのです。
続く
一人の員が直属の部下を何人持っても構いません。また、人間の多くの組織とは異なり、一人の員が直属の上司を何人持っても構いません。ただし、ある員の集まりがあるとして、その集まりの全員だけを部下に持つ上司というのが、もし居るとすればそれは唯一人しか許されない、という規則があります。言い換えると、もし員aと員bの持つ部下が全員同じであるとすれば、実は員aと員bは同一人物であるということです。これはまた、ある員の部下を全員特定すれば、その員が唯一人に特定できるということでもあります。これを正確に示すために論理記号で表せば次のようになります。
規則1. ∀x(x∈a⇔x∈b)→a=b
「その集まりの全員だけを部下に持つ上司」では長いので、簡単に「員の集まりの上司」と呼ぶことにします。もちろん直属の上司です。
この規則1のもとでは一見、員の集まりと員とが1対1に対応するように見えますが、そうではありません。まず、一人も部下のいない員がいるかも知れません。また員の集まりで、「その集まりの上司」がいない場合もあり得ます。「員の集まり自体」と「その集まりの上司」を混同しては拙いので、「員の集まり自体」はクラスと呼ぶことにします。特に「その集まりの上司」がいないクラスだけをクラスと呼ぶ場合もあります。
ではこの組織には具体的にどんな員がいるのか。

図1
一人も部下のいない員がいるかも知れないと書きましたが、実はそのような員が唯一人だけいて、φ(ファイ)という名を持っています。別名ゼロ(0)とも呼ばれます。ミスターゼロとはなかなか良い名前です。
員φだけを部下とする員もいて1(イチ)と呼ばれています。員φと員1だけを部下とする員もいて2と呼ばれています。員φと員1と員2だけを部下とする員もいて3と呼ばれています。以下同様に続き、どんな自然数nについても、員φと員1と・・・員nだけを部下とする員もいて(n+1)と呼ばれています。つまり自然数に対応するだけの無数の員がいることが判明しました。今紹介した員達はゼロから始まる自然数全てと1対1に対応しますので簡単に「自然数員」と呼ぶことにします。
さて驚くべきことに、これら無数の「自然数員」の全員だけを部下とする員もいるのです。この員は普通ω(オメガ)と呼ばれています。さらに、ωとφだけを部下とする員もいて(ω+1)と呼ばれています。と、またまた続くのですが、その前に。
例えば員4の部下は{φ,1,2,3}の4名です。この4名の中の何名かで作る集まり(クラス)は次の通りです。
{φ,1,2,3}
{φ,1,2}、{φ,1,3}、{φ,2,3}、{1,2,3}
{φ,1}、{φ,2}、{φ,3}、{1,2}、{1,3}、{2,3}
{φ}、{1}、{2}、{3}
これらの15個のクラスにも全て上司がいますが、その15人の中にはすでに出てきた員もいます。つまり、クラス{φ,1,2,3}、{φ,1,2}、{φ,1}、{φ}の上司はそれぞれ4,3,2,1です。また、この中で員3を含まない7個のクラスは実は員3の部下である{φ,1,2}の3名で作られるクラスでもあります。員3を含むクラスの上司はいわば員4と同格と言えて、「ランクが4である」と呼ばれます。
上の作り方でのランクnの員の数は(2^n-2^(n-1))となることはわかりやすいでしょう。しかし、ランクnの員はこれだけではありません。つまり下から挙げてゆくと、
ランク0 φ
ランク1 1(∋{φ})
ランク2 2(∋{φ,1})、{1}
ここで{1}、つまり員1だけを部下とする員が登場しました。この員をS{1}と名づけるとすると、ランク3の員は{φ,1,2,S{1}}の4名の中の何名かで作るクラスの上司で、ランク2以下ではない員です。
むしろランク3以下の員の数は2^4という方がわかりやすいでしょう。
一般にはランクn以下の員の数をS(n)とすれば、
S(n)=2^(S(n-1))
です。結局S(n)は次のように累乗を重ねた数になります。この表現はタワーと呼ばれます。
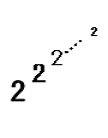
ちなみに、Tower(1)=2、としてTower(n)の値を列挙すると、
Tower(2) = 4
Tower(3) = 16
Tower(4) = 216 = 64*1024
Tower(5) = 265536≒64*10(6553*3)
逆に言うとタワーという表現は、これほどの巨大な数を実にコンパクトに表現できるのです。
続く


























※コメント投稿者のブログIDはブログ作成者のみに通知されます