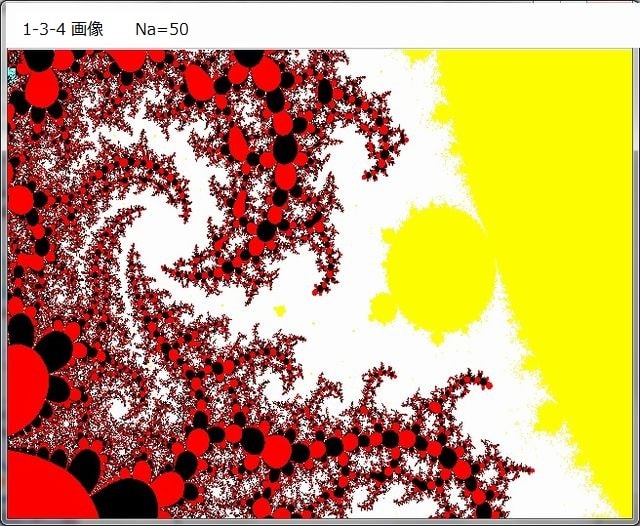
Z^2マンデルブロ集合の周辺部分の点Zm(=Xm+iYm)としたとき、Z←f(Z)+Zm のジュリィア集合画像を求める。
今回以降の記事ではf(Z)=Z^2とする。
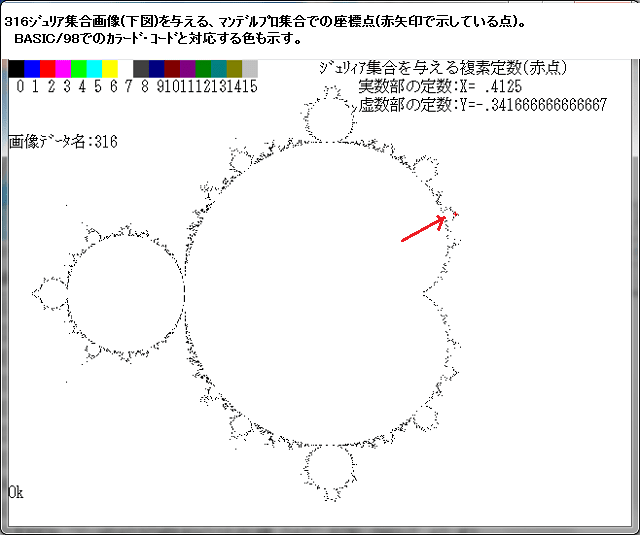
点Zmは、下図のZ^2マンデルブロ集合の周辺画像の任意の点をマウス・クリックで与えている。
但し、下図のZ^2マンデル集合周辺画像は正確なZ^2マンデルブロ集合部ではなく、その接近した外側部である。
Zm点は赤の十字マークで示している。その点が分かるように赤い線で、その位置を示している。
***
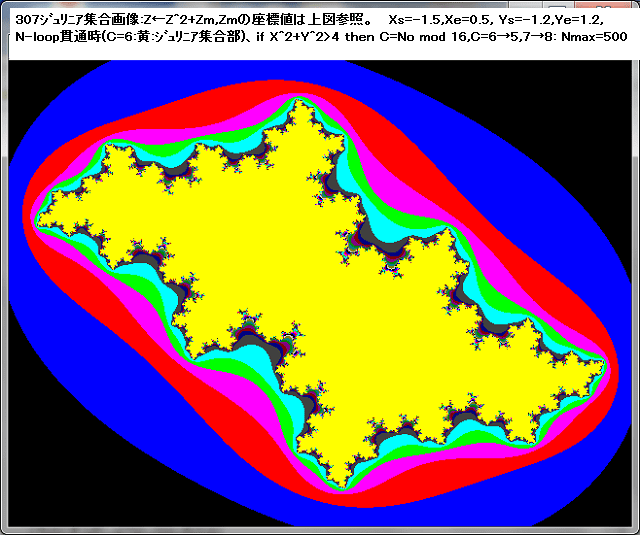
そのZm点でのジュリィア集合画像を、Z^2マンデルブロ集合周辺画像の下図に示した。
このジュリア集合画像は、Zm点を1dotでも、ずらすと変化してしまう。
ジュリニア集合画像自体が、Zm点に強く依存している。
***
下図のジュリィア集合部分は黄色(C=6)の部分であり、Z←f(Z)+Zm点列が収束する部分である。
このジュリィア集合部分の画像構造が、Zm点に強く依存しており、Z^2マンデルブロ集合の周辺で著しく変化する。
マンデルブロ集合内では、ジュリィア集合画像構造は単純な「塊(かたまり」となり、マンデルブロ集合の外側ではジュリィア集合部分は無くなる。
***
ジュリィア集合画像構造が面白いZm点は、マンデルブロ集合の近接した周辺座標であるが、その画像構造はZmで変幻自在に変化していることが分かる。
------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------

------------------------------------


------------------------------------


------------------------------------


-------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


-----------------------------------

-----------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------
今回以降の記事ではf(Z)=Z^2とする。
点Zmは、下図のZ^2マンデルブロ集合の周辺画像の任意の点をマウス・クリックで与えている。
但し、下図のZ^2マンデル集合周辺画像は正確なZ^2マンデルブロ集合部ではなく、その接近した外側部である。
Zm点は赤の十字マークで示している。その点が分かるように赤い線で、その位置を示している。
***
そのZm点でのジュリィア集合画像を、Z^2マンデルブロ集合周辺画像の下図に示した。
このジュリア集合画像は、Zm点を1dotでも、ずらすと変化してしまう。
ジュリニア集合画像自体が、Zm点に強く依存している。
***
下図のジュリィア集合部分は黄色(C=6)の部分であり、Z←f(Z)+Zm点列が収束する部分である。
このジュリィア集合部分の画像構造が、Zm点に強く依存しており、Z^2マンデルブロ集合の周辺で著しく変化する。
マンデルブロ集合内では、ジュリィア集合画像構造は単純な「塊(かたまり」となり、マンデルブロ集合の外側ではジュリィア集合部分は無くなる。
***
ジュリィア集合画像構造が面白いZm点は、マンデルブロ集合の近接した周辺座標であるが、その画像構造はZmで変幻自在に変化していることが分かる。
------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


-------------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------


-----------------------------------


-----------------------------------


------------------------------------


------------------------------------


------------------------------------


------------------------------------