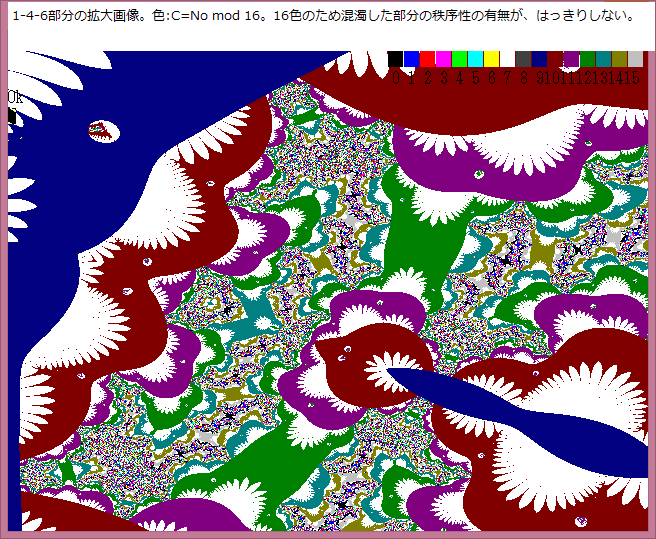
今迄の画像の色は、N-loop内で発生する循環点列:Z0,Z1,Z2,・・・がN-loopを脱出するときのNをNoとすると、色:C=No mod 16 としてきた。BASIC/98では16色しか使えないので画像は16色で表示している。
これまでの画像の全てに言えることだが、画像の色と其のカラーコード番号を見れば分かるように画像の色構造は或る秩序がある。その秩序とは、画像の中の『一つ部分』の色をNaとすると『其の部分に隣接する部分』の色は、Na+1 または Na-1 となっている。
その様子の典型画像が、今迄の画像に現れた「ら線階段」で、其の画像は『一つの部分』でNo=Naとすると、『隣接した右の部分』は No=Na+1となって、その「ら線階段」は或る収束点へと収斂している。
そのような画像構造は此のブログの画像の全てに見られる構造だが、Z^Z+0.026画像も其の例にもれない。
このように画像構造を単純化して見る方法に、Noが偶数ならば赤、奇数ならば黒のようにして画像をシンプルにする方法がある。こうすると画像の構造が明瞭になる。例えばマンデルブロ画像の画像構造を見る場合に有効である。
このように画像の色をシンプルにすると其の画像の構造が分かり易くなる。但し、Z^Z+0.026画像の場合、白色部分はNo>Nmaxとなり、N-loopを貫通してしまう部分である。
***
さて前記事の Z^Z+0.026 画像の色を以下のように単純化して見ることにする。
『もし、No>=Na ならば、No=偶数→赤、No=奇数→黒とする。
そして、もし、No<Na ならば、No=偶数→青、No=奇数→緑とする。
但し、白色部分はpset条件を満足しない場合の部分である。』
こうすることによって、
1.画像のNoが厳密に1ずつ変化していること。
2.画像の「ら線構造」「楕円の重層構造」等。
3.Noの分布構造。
が明瞭になる。
------------------------------------