PCが描く奇妙な画像集(数学的万華鏡と生物形態等の世界)

・インタープリタBASICによるフラクタルとカオスの奇妙な画集。

365 連続したジュリィア集合画像(その1)

2014-08-04 08:46:12 | ジュリィア集合
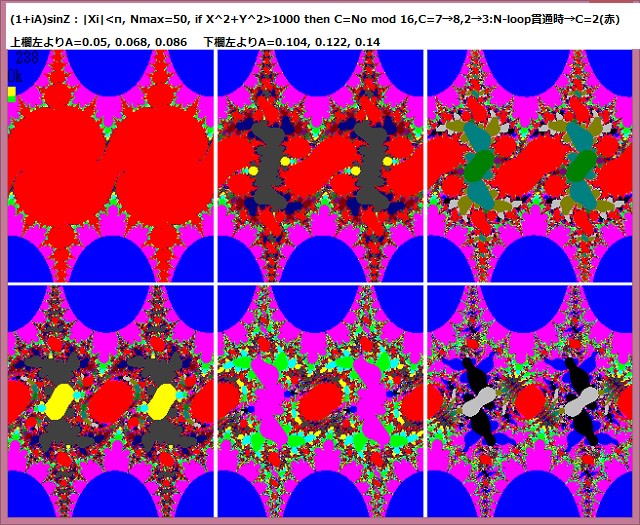
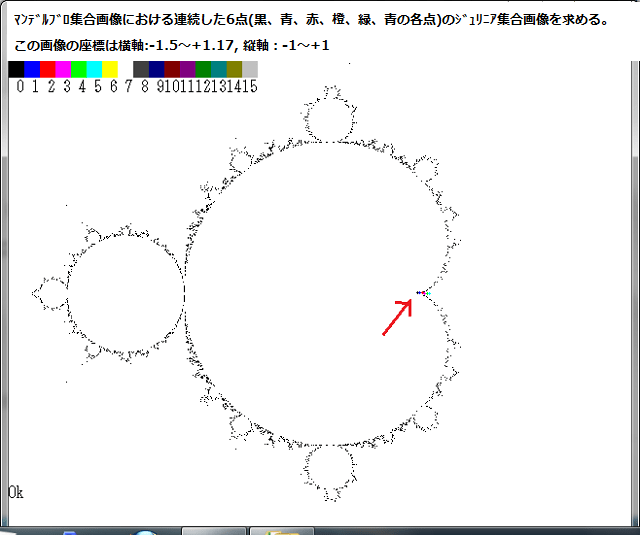
点列：Z←Z^2+Zcにおいて、Zcを任意の線分を6等分したときの各点を、黒、青、赤、橙、緑、青で示したとき、それらのZcで生成されるジュリィア集合全体画像を下図に示す。
ZcはZ^2マンデルブロ集合の周辺や其の内部・外部の点を任意に選び、それらの点に対応したジュリィア集合全体画像やジュリニア集合そのものを示す。
***
下図から分かるように、Z^2マンデルブロ集合の内部のZcでは、ジュリニア集合そのものは、ひと塊となった形態となり、その形態は点Zcに依存している。Z^2マンデルブロ集合の周辺では、ジュリニア集合そのものの形態は複雑に入り組んだものとなり、その複雑はZcに強く依存している。

しかし、基本的な形態は近接したZcでは、N-loop脱出時の形態は不変で、変化するのは脱出時のNoで其れが、色C=No mod 16として変化している。N-loop貫通部分がジュリニア集合そのものとなるが、それは
No→Nmax(=500)の場合であるから、ジュリニア集合そのものの画像は、N-loop脱出時の形態の中に含まれる。
***





***





***







***







***







***








364 複素関数：(1+iA)cosZ で実変数Aを変えた時のジュリィア集合の変化

2014-08-04 08:31:49 | ジュリィア集合
複素関数：(1+iA)cosZ において、Aを実数として変化させた時の、ジュリィア集合の変化を調べる。
但し、ここで、Nmax=50として、N-loop脱出(発散)条件を、X^2+Y^2>1000としたときとし、その場合の色を、C=No mod 16,C=7→8,2→3とする。N-loop貫通時にはC=2(赤)とし、その赤部分をジュリィア集合とする。(注：この条件を変えればジュリィア集合の形態は変わってくるが、ここでは上記の場合をジュリィア集合と定義する。)
***
この場合の、Aを変化させた時の図を下に示す。Aが大きくなるにつれて、ジュリィア集合は分散していく様子が分かる。

***
(1+iA)cosZの実数部と虚数部を求める計算は参考として最後に書いておく。
***





***

下図はAの範囲を大きくした場合。





---------------------------------------
(参考)　

(1+iA)cosZの実数部と虚数部を求める計算は下記のとおり。
f(Z)=(1+iA)sinZ=(1+iA)(sinXcoshY+icosXsinhY)
従って、
Re.f(Z)=sinXcoshY-AcosXsinhY
Im.f(Z)=cosXsinhY+AsinXcoshY

363 サンマルコ・ジュリニア集合画像と其の部分拡大図

2014-08-04 08:25:42 | ジュリィア集合
サンマルコ画像と言われている画像がある。これはジュリィア集合画像であるが、その形がサンマルコ聖堂に似ているから、そう言われるのだろう。以下の画像が私流の其の画像である。画像条件は以下のとおり。
***
複素関数：coshZ-2.25
発散条件と色：if X^2+Y^2>2500 then 色C=No mod 16,C=7→8,2→3,Nmax=40
収束時(即ちN-loop貫通時。此れがジュリニア集合部分となる)→C=2(赤)とする。
画像表示座標：XS=-4.2,Xe=4.2,Ys=-3.15,Ye=3.15

***

下図から分かるように、ミニ・サンマルコ・ジュリニア集合(赤色)が随所に存在する。



***





-----------------------------------------










362 マンデルブロ集合周辺部のジュリニア集合画像 (その3)

2014-08-04 08:12:03 | ジュリィア集合
Z^2マンデルブロ集合周辺部のジュリニア集合の全体画像及びジュリニア集合そのものの画像を示す。
下図のマンデルブロ画像の周辺画像は厳密には周辺ではなく、その概略を示すもので、Z^2マンデルブロ集合の真の周辺より外部にある。

***
複素平面の点をZmとするとき、点列：Z←Z+Zmが発散しない場合、即ち、N-loopを貫通する場合には、その点Zmに対応したジュリニア集合が存在し、点Zmが異なれば、その場合のジュリニア集合の形態も異なってくる。
------------------------------------------



-------------------------------------------





-------------------------------------------





--------------------------------------------





-------------------------------------------





------------------------------------------



------------------------------------------



------------------------------------------



------------------------------------------



------------------------------------------





-----------------------------------------





-----------------------------------------



----------------------------------------





-----------------------------------------



---------------------------------------------

361 記事357において、ジュリィア集合のみの表示

2014-08-04 07:47:28 | ジュリィア集合
前記事360同様に 記事357において、ジュリィア集合のみの表示する。

なお、下図のマンデルブロ画像の周辺画像は厳密には周辺ではなく、その概略を示すもので、Z^2マンデルブロ集合の真の周辺より外部にある。
-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



-----------------------------------------------



----------------------------------------------



----------------------------------------------



-----------------------------------------------



----------------------------------------------



---------------------------------------------



---------------------------------------------



---------------------------------------------



---------------------------------------------



--------------------------------------------