370 いろいろなジュリィア集合画像

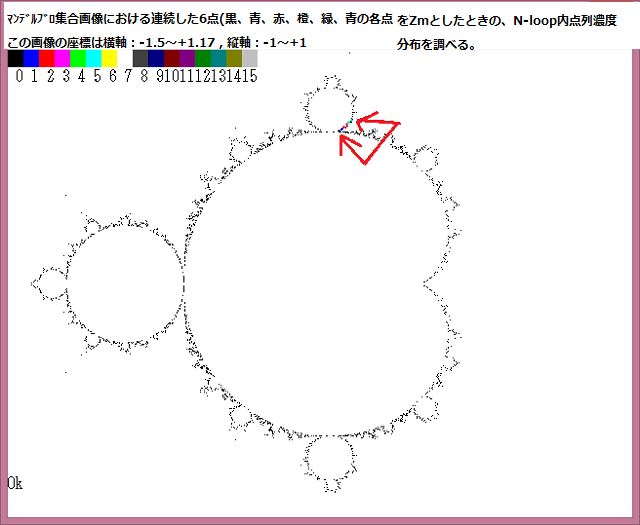
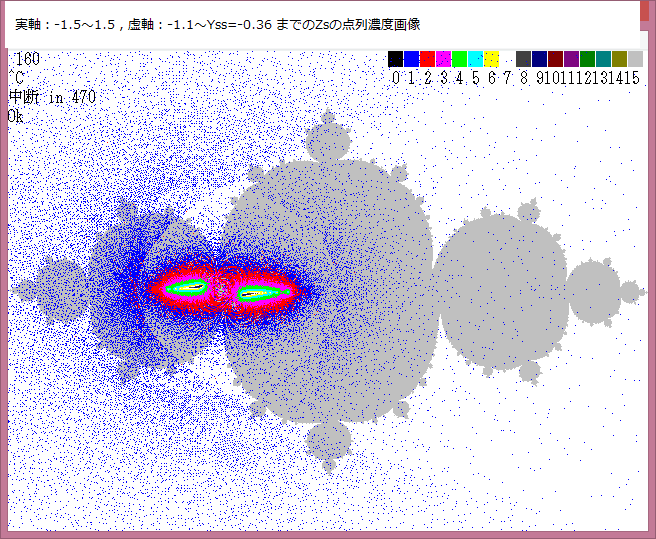
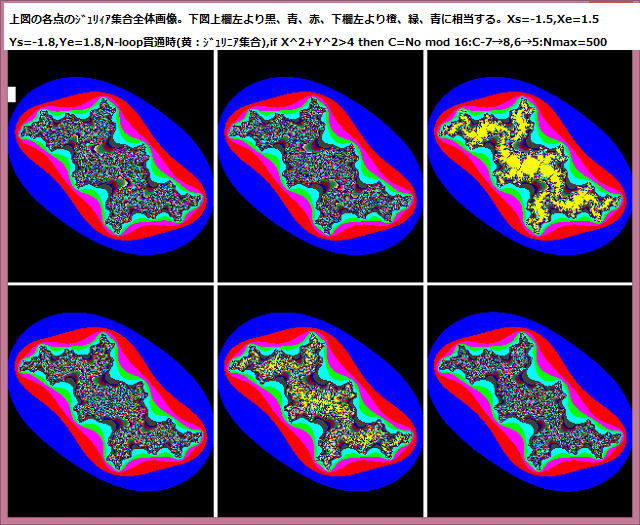
いろいろなジュリィア集合画像を示す。詳しい解説は記事367参照。　
--------------------------------------------------







--------------------------------------------------







-------------------------------------------------







-------------------------------------------------







------------------------------------------------

***





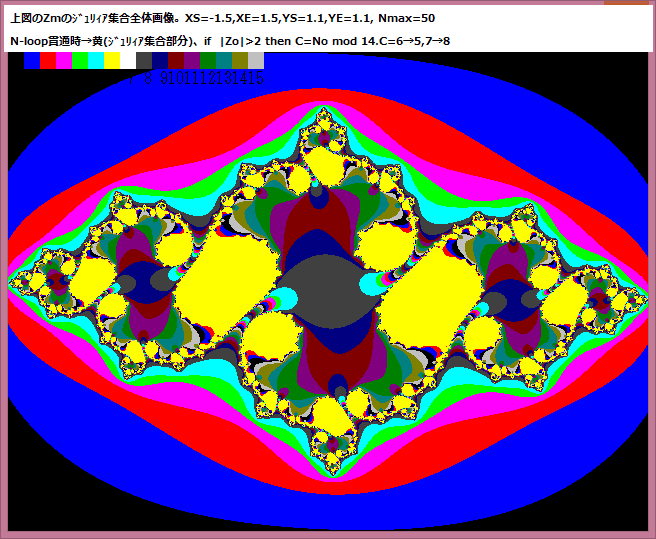
166 167 168

***

369 6連続したジュリィア集合のN-loop内での点列濃度分布

記事366の、6連続したジュリィア集合画像の、N-loop内での点列濃度分布画像を求める。
詳細な説明は記事367の解説を参照。
***
ジュリィア集合と其の点列画像を重ね描きするが、点列画像がジュリィア集合画像を覆い、その位置関係が不明になるため、ジュリィア集合に対して点列が、どのように変化していくかを見るために、今回は領域Dにおいて、実軸は -1.5～1.5 で、虚軸はパラメータ:Yssを用いて-1.8～Yss までのZs の点列濃度画像を順次示していく。Yssの最終値はYs=1.8である。

***
以下の画像より、3箇所の点列集中点(アトラクタ点)が存在することが分かる。
また其のアトラクタ点の周囲には不規則な点が存在していることが分かる。
これらの点はYssが小さい場合：(-1.8～約-0.99 )には、一種の規則性をもった点列軌道を示している。
***
また、Yss=1.8の全体画像での濃度(m)の最大値は、C=12となるから、m=e^11.5～e^12.5=98715～268337の範囲にあることが分かる(なお、このジュリィア集合画像のNmaxは500である)。

-----------------------

368 ジュリィア集合のN-loop内での点列濃度分布(その2)

この画像の詳細な説明は前記事367を参照。
***
ジュリィア集合に対して点列が、どのように変化していくかを見るために、今回は領域Dにおいて、実軸は -1.5～1.5 で、虚軸はパラメータ:Yssを用いて-1.1～Yss までのZs の点列濃度画像を示す。Yssの最終値はYs=1.1である。
***









----------------------------











-----------------------------
以上の画像から分かるように、点列濃度は、2箇所の座標点付近に大きくなっている。
これは点列軌跡が此の座標点付近を頻繁に通過していることを意味しており、一種のアトラクタとなっている。全体の点列濃度画像では、最大濃度は C=10 となっており、濃度：m=e^9.5～e^10.5=13360～36315 の範囲にあることが分かる。

また、2箇所の点列軌跡集中点以外に、画像領域：D 内で、青色(C=1)の、不規則な点と規則性をもった点が Yss=-0.56あたりから目立つようになる。

367 ジュリィア集合での点列濃度(その1)及び解説

或る与えられた複素平面領域 D の点をZsとする。また任意の複素定数をZmとする。
D の領域は実軸は　-1.5～1.5 、虚軸は　-1.1～1.1　とする。
ここで、Zsを始点とする再帰点列：Z←Z^2+Zmを考えると次の点列が得られる。

Z0,Z1,Z2,Z3,・・・,ZN,・・・　　・・・(1)

ここで、Z0=Zs^2+Zm ,Z1=Z0^2+Zm,・・・・である。

今、この点列の数の上限を設け其れをNmaxとする。

Nmax以下の或るNoで、|ZNo|>2の場合、点列は発散すると定義する。

また、Nmax以下の如何なるNでも|ZN|




















--------------------------------------------------------------------
上図から分かるように、ジュリィア集合内の全てのZsの点列の濃度は、ジュリィア集合画像の特定の部位に集中している。その最大濃度値はC=8だから、m=e^7.5～e^8.5=1807～4914の範囲にある。また点列は領域 D の全域に渡って存在している。青色の部分(C=1)の濃度は、e^0.5～e^1.5=1.6～4.5
の範囲にある。

366 連続したジュリニア集合画像 (その2)

前回の記事365とは、異なる座標値Zcに関するジュリニア集合画像である。







--------------------------------------






---------------------------------------







----------------------------------------







----------------------------------------







---------------------------------------







--------------------------------------







--------------------------------------







--------------------------------------







-------------------------------------







-----------------------------------