508 Z^Z+0.2 画像

画像の作成条件は以下のとおり。

1.複素関数：Z^Z+0.2　
2.元図のN-loop入力範囲：横軸は -4～+4 縦軸は -1.7～+3
3.N-loop脱出条件：(X^2+Y^2)＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

----------------------------------------






--------------------------------------

507 Z^Z+0.125 画像 (N-loop条件の変更)

N-loop条件を、『(X^2+Y^2)^0.5＞100 ならば脱出する』に変更した画像。

--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Z+0.1　
2.元図のN-loop入力範囲：横軸は -3.5～+3.5 縦軸は -3.5～+1.75
3.N-loop脱出条件：(X^2+Y^2)^0.5＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

------------------------------------

506 Z^Z+0.1 画像の中の部分の拡大画像(その2)

前記事にて時計方向に90度回転させた、Z^Z+0.1 画像の中の5か所の部分を拡大する。時計方向に90度回転させた画像のほうが画像構造が見やすいため、この回転画像の中の5か所の部分を選び其れを拡大して見る。

--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Z+0.1　
2.元図のN-loop入力範囲：横軸は -3.5～+3.5 縦軸は -3.5～+1.75
3.N-loop脱出条件：(X^2+Y^2)＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

-------------------------------





------------------------------

505 Z^Z+0.034 画像の中の部分の拡大画像(その2)

前記事にて時計方向に90度回転させた、Z^Z+0.034 画像の中の4か所の部分を拡大する。時計方向に90度回転させた画像のほうが画像構造が見やすいため、この回転画像の中の9か所の部分を選び其れを拡大して見る。

それらの拡大画像から分かるように、Z^Z+0.034 画像は独特な「ら線画像」が、いたる箇所に存在するフラクタル構造となっている。
--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Z+0.034　
2.元図のN-loop入力範囲：横軸は -3.5～+3.5 縦軸は -3.5～+1.75
3.N-loop脱出条件：(X^2+Y^2)＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。






-----------------

504 Z^Z+μ画像(90度回転したデカルト座標表示)その2

記事502に掲載した画像を90度時計回りに回転させた画像を示す。

--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Zμ, μ=0.034, 0.042, 0.05, 0.075, 0.1　
2.N-loop入力範囲：横軸：-3.5～+3.5, 縦軸：-3.5～+1.75
3.表示範囲(N-loop入力範囲)：(X^2+Y^2)＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

-------------------------------------

503 Z^Z+0.034 画像の中の部分の拡大画像

Z^Z+0.034 画像の中の4か所の部分を拡大する。
--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Z+0.034　
2.N-loop入力範囲：元図に書いてある。
3.N-loop脱出条件：(X^2+Y^2)＞100 ならば脱出する。Nmax=500
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。



-----------------------


------------------------

502 Z^Z+μ画像(デカルト座標表示)その1

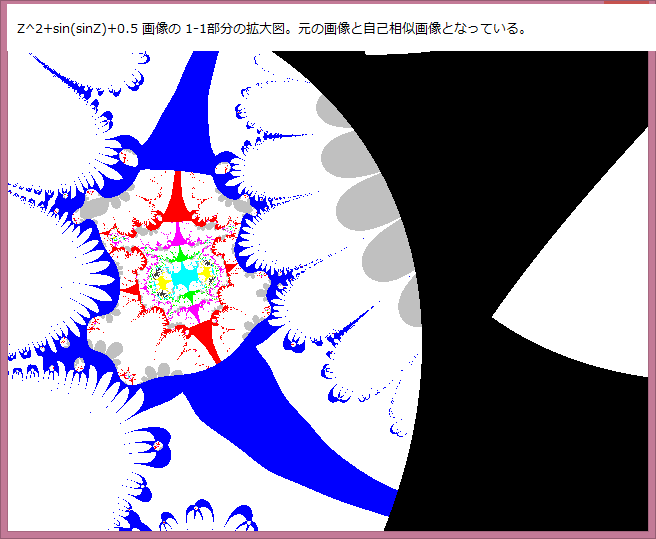
今迄、複素関数：Z^Z関連の各種の画像を調べてきた。
今回の画像は、脱出後の pset 条件を以下のように変える。
・N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。

今迄の画像においては以下のようにした。
・N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。

この条件の変化によって画像が、かなり変化する。
--------------------------------------
以下画像の作成条件は以下のとおり。

1.複素関数：Z^Z+μ　：μの値は各図に書いてある。
2.N-loop入力範囲：Xs,Xe,Ys,Ye の値は各図に書いてある。
3.N-loop脱出条件：(X^2+Y^2)＞100 ならば脱出する。Nmax=50 or 100
4.N-loop脱出後のpset条件：(|X|＜100 or |Y|＜100)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

------------------------------------
画像の最後にBASIC/98のプロクラム例を書いておく。　
注：以下の画像で　(X^2+Y^2)^0.5>100は(X^2+Y^2)>100 の誤りである。
------------------------------------








-----------------------------------













-----------------------------------------------------------------
BASIC/98での画像作成プログラム例

10 REM Z^Z+C
30 CHAIN MERGE "C:\BASIC\PRO\SUBR\KOSHIKI.BAS",40,ALL
40 CHAIN MERGE "C:\BASIC\PRO\SUBR\ARCTAN3.BAS",50,ALL
50 CHAIN MERGE "C:\BASIC\PRO\SUBR\Z^ZA.BAS",51,ALL
51 CHAIN MERGE "C:\BASIC\PRO\SUBR\ER1.BAS",60,ALL
60 ON ERROR GOTO 50000
90 CONSOLE ,,0,1
100 COLOR 0,7,,,2
110 CLS 3
120 GOSUB 10000
210 XS=-3.5 :XE=3.5
220 D=(XE-XS)/640:DX=D:DY=D:YS=-240*DY:YE=-YS
240 FOR J=0 TO 480
260 FOR K=0 TO 640
270 X=XS+DX*K
280 Y=YS+DY*J
290 FOR N=0 TO 50
300 R=SQR(X^2+Y^2)
310 GOSUB 5000
320 GOSUB 9000
330 X=ZZR+0.1
340 Y=ZZI
350 Q=X^2+Y^2
360 IF Q>100 THEN 400
370 NEXT N
380 C=15
390 GOTO 430
400 IF ABS(X)<100 OR ABS(Y)<100 THEN 410 ELSE 460
410 C=N MOD 16
420 IF C=7 THEN C=8
430 REM
440 PSET(K,J),C
450 WRITE #1,K,J,C,N
460 NEXT K
470 NEXT J
500 END

501 放散虫：Z^2+sinZ+0.5 の仲間とフラクタル性

複素関数:Z^2+f(Z)+0.5 において、f(Z)がsinに関連する関数について調べてみる。
即ち、f(Z)=sinZ, sinhZ, e^sinZ, sin(sinZ) の画像を作る。

これらの関数は、sinZ と数学的に関連があるというより、sin が当該関数に含まれているという理由だけで選んだ。しかし、画像を見てみると其の画像構成は或る類似性があり面白い。

この画像の作成条件は以下のとおり。

1.複素関数：Z^2+f(Z)+0.5 ,f(Z)=sinZ, sinhZ, e^sinZ, sin(sinZ)
2.N-loop入力範囲：Xs=-4.5,Xe=3,Ys=-2.8,Ye=2.8
3.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=50 or 100
4.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

以下に、Z^2+f(Z)+0.5 ,f(Z)=sinZ, sinhZ, e^sinZ, sin(sinZ) の画像を順に示す。各画像の中の部分も拡大してみる。

------------------------------------------------------------
・Z^2+sinZ+0.5 画像








------------------------------------------------------------
・Z^2+sinhZ+0.5 画像







------------------------------------------------------------
・Z^2+e^sinZ+0.5 画像











------------------------------------------------------------
・Z^2+sin(sinZ)+0.5 画像











---------------------------------------------------
以上の画像より部分の画像が元の画像の相似となっているフラクタル性があることが分かる。こんなところにも、という意外な箇所にも自己相似の画像が存在し驚く。そもそも此れらの画像作成プログラムは「自己回帰、即ちN-loop」が本質だから、そのようなフラクタル性は当然であるとも言える。しかし、そうであるにせよ、この自己回帰性のもつ創造性、豊潤性さには目を見張るものがある。

500 e^(Z^s)+0.5画像の s による変容画像

今回の画像は複素関数が、e^(Z^s)+0.5 のとき、s を 2→7 にしたときの画像の変容を調べる。

この画像の作成条件は以下のとおり。

1.複素関数：e^(Z^s)+0.5,s=2,3,4,5,6,7
2.N-loop入力範囲：Xs=2,Xe=2,Ys=-2.2,Ye=2.2
3.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=100
4.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
5.N-loop貫通時は、C=15とする。

--------------------------------------------------------------
下図から分かるように、e^(Z^s)+0.5 画像は放物線の図形によって見事に s 分割されている。

499 Z^s+e^sinZ+μ画像の s による変容画像

今回の画像は複素関数が、Z^s+e^sinZ+0.5 のとき、s を 2,3,4,5,6,7 にしたときの画像の変容を調べる。

この画像の作成条件は以下のとおり。
1.複素関数：Z^e^sinZ+μ,s=2, 3,4,5,6,7:μ=0.5 or 1
2.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。





下図は上図の、s=2　の場合の画像。

498 Z^s+sin(sinZ)+0.5画像の s による変容画像

今回の画像は複素関数が、Z^s+sin(sinZ)+0.5 のとき、s を 2,3,4,5,6,7 にしたときの画像の変容を調べる。

この画像の作成条件は以下のとおり。
1.複素関数：Z^s+sin(sinZ)+0.5,s=2, 3,4,5,6,7
2.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。

-----------------------------------



上図を離れて見ると・・・　




以下の画像は、s=2 及び s=3 の場合の拡大図である。　　

497 Z^s+sinhZ+0.5画像の s による変容画像(その1)

今回の画像は複素関数が、Z^s+sinhZ+0.5 のとき、s を 2→13 にしたときの画像の変容を調べる。

この画像の作成条件は以下のとおり。
1.複素関数：Z^s+sinhZ+0.5,s=2, 3,4,5,6,7,8,9,10,11,12,13
2.N-loop脱出条件：X^2+Y^2＞100 ならば脱出する。Nmax=50
3.N-loop脱出後のpset条件：(|X|＜10 or |Y|＜10)　ならばpsetする。
N-loop脱出ときのN値をNoとすると、psetの色:CはC=No mod 16 とする。
但し、C=7ならばC=8とする。
4.N-loop貫通時は、C=15とする。

496 Z^2.6画像の中の変容部分の画像のフラクタル性

Z^2.4画像における画像形態の変容画像を記事493に示した
下の画像から分かるように拡大部分の画像は、元の画像と自己相似(フラクタル)な形態となっている。更に其の中の部分も自己相似(フラクタル)な形態となっていることが分かる。このようなフラクタル性は画像を如何に拡大していっても続いているらしい。この性質は画像作成アルゴリズムが自己回帰になっているのだから当然と言える。

なお各拡大画像の相似図形において色が異なるのは、N-loop脱出のN値(Noとする)が異なるためである。色:C=No mod 16 としている。







----------------------------------





下図は1-1図の回転画像。いかにも「放散虫」らしく見える。