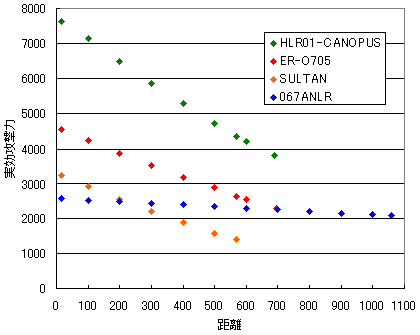
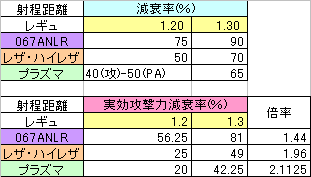
Part1レギュ1.30でのAA攻撃力計算に先立ち
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる
Part7はPart6で求めたAA攻撃力の補足事項です。ZやらBやらCやらの記号の使い方はPart6までを参照。PA満タン以外でも成立させます。
まず、予備知識として、アサルトアーマーの攻撃力が決定されるのは攻撃判定が出る直前(判定出るのとほぼ同時とも)です。PAフル時に同じ機体が大体同時にAAを発動した場合、1フレームズレると攻撃力が変わる(遅れた方が攻撃力が下がる)のは、遅れることで相手のAAによってPAが減少するからです。
この事実は、コマンド入力してAAを発動した時点では、まだ攻撃力が決定されていないという証明でもあります。
これを利用すると、PAゲージが0%状態でのアサルトアーマーの攻撃力が求められます。コマンドを入力→攻撃判定が出るまでの間に、なんらかの手段でAA使用側のPAを減衰させて0%にすればよい。PA干渉させて減衰させたり(6ヒット測定限定)、プラズマで一気にPAを剥ぐなり、AA使用者自身がコジマチャージしてAA発動中もPAを減少させ続けたり。私はコジマチャージを利用しました。
なお、AAのコマンドを入力した瞬間にジェネレータのKP出力は0になります。PAゲージ0%で測定する上でも重要ですが、これはPA崩壊→PA再展開した瞬間のAA攻撃力≒PAゲージ30%時のAA攻撃力を求める上で念頭に置かなければならないことです。PAが再展開する瞬間にAAコマンドをして攻撃力を求める場合、同時にコジマチャージをしているとKP出力が0になり、チャージでKPが消費されることでPAが減少してしまい、結果が過小評価されてしまいます。PAゲージ30%になるべく結果を近づけるには、他に余計なことはせずにKP出力が低いジェネレータでAAするのが賢明でしょう。
PAゲージ30%を測る理由は、0%と100%の間にひとつ測定点を加えることで、近似直線(もしくは曲線)の振る舞いがどうなっているか確認するためです。0と100だけでは信頼性に欠ける。
とりあえず、今回はPAについて見るだけなので、AA攻撃力/OBはKRB-SOBREROの4000で固定。式の大まかな形は分かっているのでこの数値まで変える必要は現時点では無い。不都合が出てから初めて変更すればよい。
AAを当てる対象はEN防御最低機体(EN防御3828)。最大誤差を減らすためのお決まりの方法。EN攻撃力=ENダメージ/(1-EN防御/13000)で攻撃力算出。
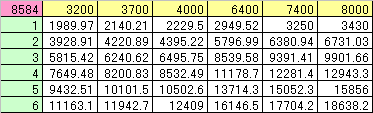
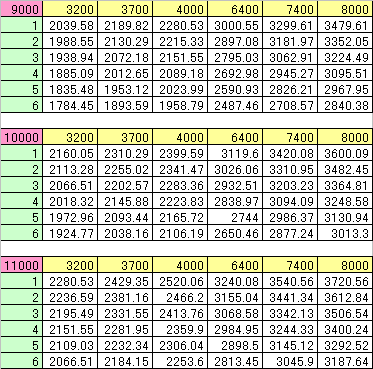
PAゲージ0%時の総合AA攻撃力(6ヒット)の実測値
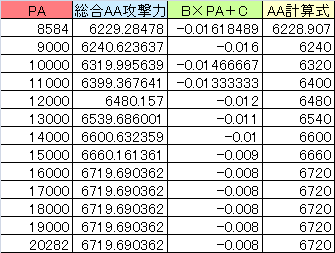
PA:測定した機体のPA
総合AA攻撃力:実測して算出、誤差は
B×PA+C:Part6まで使ってきた式、
AA攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA
のB×PA+Cの部分の値。
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
より算出。
AA計算式:これより後で求めますが、分割するのめんどくさいので載せておく。実測値との誤差が全て1.41736(EN防御最低機体のAP1のズレで生じうる最大誤差)以内なのでまあ一致している。
まず、PAに対する総合AA攻撃力(PAゲージ0%時)の実測値ですが、

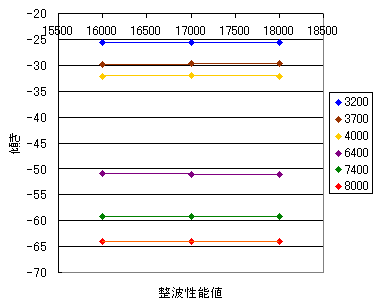
どこかで見覚えのある形になりました。ここで、B×PA+Cを計算した図を示します。

領域こそ異なるものの、傾向は全く同じと言ってもよいでしょう。
PAゲージが0%のときの6ヒットの総合AA攻撃力について、各領域(PA≦9000、9000≦PA≦12000、12000≦PA≦16000、16000≦PA)の近似直線(AA計算式)を求めます。
まず、16000≦PAについては、実測値が6719.69≒6720。AA計算式=6720の定数と言ってさしつかえないでしょう。
12000≦PA≦16000では、PAが1000変わると実測値がほぼ60変化しています。傾きは60/1000=3/50と言えます。ここから切片は5760、近似直線は
AA計算式=3/50×PA+5760。
9000≦PA≦12000では、PAが1000変わると、実測値はほぼ80変化しています。傾きは80/1000=2/25、切片は5520、近似直線は
AA計算式=2/25×PA+5520。
PA≦9000ですが、PA8584とPA9000の二つだけでは範囲も500以内と狭く、いまいちよくわかりません。しかしながら、先ほど、B×PA+Cと傾向が同じだろうと述べました。これを利用してみましょう。Bの値がちょうど傾きと同じ意味ですからBを比べます。
12000≦PA≦16000では 1.0×10^(-6)。
9000≦PA≦12000では 2/15×10^(-5)で12000≦PA≦16000における数値の4/3倍。
PA≦9000では、2/45×10^(-5)で9000≦PA≦12000における数値の1/3倍。
AA計算式の方の傾きも、実は9000≦PA≦12000における数値(2/25)の1/3倍の2/75ではないか、という推測がなされます。
試しに2/75を代入してみると、切片は6000。2/75×PA+6000という式になります。これはPA8584、PA9000の両方について見たところ、実測値との大きな誤差はありません。この式で問題無いようです。
一方、Part6までの総合AA攻撃力の式は、
総合AA攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA]
でした。
ここで、0.12×PAを0にしてみた、
Z×{(Z-1)(B×PA+C)/2+0.30}×AA
を計算してみましょう。Z=6、AA=4000で、各PA領域でのBとCを用います。
「計算結果」とでもすると、

コピペではないです。まったく同じになりました。
これが6ヒット限定のものではないという一例として、PA15000について、PAゲージ0%での1~6ヒット全てについて軽く見てみましょう。計算ってついていないのは実測値から求めたもの、ついているのは計算して求めたもの。

最大誤差以内で一致します。
どうやらこの式で問題ないようです。PAゲージが0%のとき、
総合AA攻撃力=Z×{(Z-1)(B×PA+C)/2+0.30}×AA
0%のときに青式のようになったということは、PAゲージの割合によって、
今まで0.12×PAとしていた項が変化していると考えられます。
0%のときに0。100%のときに初期PAそのままが計算に関与するということは、
0.12×PA×PAゲージの割合
ではないか、という推測が出来ます。100%なら割合は1.00、50%なら0.50といったように。
この推測を裏付けるために、0%と100%の間の、何か特定のPA割合について調べてみると安心があります。0、1.00以外で分かりやすいポイントはPA再展開の瞬間(PAゲージの割合≒0.30)しかありません。これを調べましょう。
いったんPAを剥がしたあと、PAが再展開する瞬間にAAという手法です。どうしても人の手による関係で、PAが再展開してからAAが発動するまでの間にごくわずかながらPAが30%より多くなる→AA攻撃力が多少大きく評価されます。そのため、細かいことはさておき、0%と100%の攻撃力を結んだ直線上におおむね値が乗っていれば良いと考えます。要は、変な曲線にさえなっていなければいい。
各PA領域から1例ずつ測定(水色枠はPA値)。0%と100%は計算値で30%のだけ実測値。


直線上に乗っているようなのでとりあえず問題ないとみなします。体感で0.1~0.2秒ずれると20~40ぐらいの攻撃力の差が出ます。こだわる必要もないしそんなに頑張って測っていないです。ある程度の過大評価は構わない、過小評価が出なければとりあえずよい。
計算値は左からそれぞれ8083.05、8776、9900、10824です。
直線上に乗っていることが言えたので、単純な割合で計算できることがわかりました。
ということで、改めて、
段数=Z (1~6の整数値)、初期整波性能値=PA、AA攻撃力/OB=AAとして、初期PAによって値のとり方の異なる定数B、C、PAゲージの割合(0~1)を用いると、
アサルトアーマー攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA×PAゲージの割合
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
P-MARROW装備時はAA→AA×2.00になる(レギュ1.30現在)
多段ヒットの場合、
総合アサルトアーマー攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA×PAゲージの割合]
ただし、ダメージが2倍になる現象等は未発生とし、水平面でのみ保証されるものとする。
PAゲージの割合≒(現在PA-初期PA×0.777)/(初期PA×0.223)より、
0.12×PA×PAゲージの割合≒0.12×(現在PA-初期PA×0.777)/0.223
に近似されるが、式が複雑になるため、普通に割合で考えた方がいいと思います。
Part216000≦PAのAA攻撃力式
Part312000≦PA≦16000のAA攻撃力式
Part49000≦PA≦12000のAA攻撃力式
Part5PA≦9000のAA攻撃力式
Part6AA攻撃力計算式まとめ
Part7PA満タン以外でも計算式を成立させる
Part7はPart6で求めたAA攻撃力の補足事項です。ZやらBやらCやらの記号の使い方はPart6までを参照。PA満タン以外でも成立させます。
まず、予備知識として、アサルトアーマーの攻撃力が決定されるのは攻撃判定が出る直前(判定出るのとほぼ同時とも)です。PAフル時に同じ機体が大体同時にAAを発動した場合、1フレームズレると攻撃力が変わる(遅れた方が攻撃力が下がる)のは、遅れることで相手のAAによってPAが減少するからです。
この事実は、コマンド入力してAAを発動した時点では、まだ攻撃力が決定されていないという証明でもあります。
これを利用すると、PAゲージが0%状態でのアサルトアーマーの攻撃力が求められます。コマンドを入力→攻撃判定が出るまでの間に、なんらかの手段でAA使用側のPAを減衰させて0%にすればよい。PA干渉させて減衰させたり(6ヒット測定限定)、プラズマで一気にPAを剥ぐなり、AA使用者自身がコジマチャージしてAA発動中もPAを減少させ続けたり。私はコジマチャージを利用しました。
なお、AAのコマンドを入力した瞬間にジェネレータのKP出力は0になります。PAゲージ0%で測定する上でも重要ですが、これはPA崩壊→PA再展開した瞬間のAA攻撃力≒PAゲージ30%時のAA攻撃力を求める上で念頭に置かなければならないことです。PAが再展開する瞬間にAAコマンドをして攻撃力を求める場合、同時にコジマチャージをしているとKP出力が0になり、チャージでKPが消費されることでPAが減少してしまい、結果が過小評価されてしまいます。PAゲージ30%になるべく結果を近づけるには、他に余計なことはせずにKP出力が低いジェネレータでAAするのが賢明でしょう。
PAゲージ30%を測る理由は、0%と100%の間にひとつ測定点を加えることで、近似直線(もしくは曲線)の振る舞いがどうなっているか確認するためです。0と100だけでは信頼性に欠ける。
とりあえず、今回はPAについて見るだけなので、AA攻撃力/OBはKRB-SOBREROの4000で固定。式の大まかな形は分かっているのでこの数値まで変える必要は現時点では無い。不都合が出てから初めて変更すればよい。
AAを当てる対象はEN防御最低機体(EN防御3828)。最大誤差を減らすためのお決まりの方法。EN攻撃力=ENダメージ/(1-EN防御/13000)で攻撃力算出。
PAゲージ0%時の総合AA攻撃力(6ヒット)の実測値

PA:測定した機体のPA
総合AA攻撃力:実測して算出、誤差は
B×PA+C:Part6まで使ってきた式、
AA攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA
のB×PA+Cの部分の値。
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
より算出。
AA計算式:これより後で求めますが、分割するのめんどくさいので載せておく。実測値との誤差が全て1.41736(EN防御最低機体のAP1のズレで生じうる最大誤差)以内なのでまあ一致している。
まず、PAに対する総合AA攻撃力(PAゲージ0%時)の実測値ですが、

どこかで見覚えのある形になりました。ここで、B×PA+Cを計算した図を示します。

領域こそ異なるものの、傾向は全く同じと言ってもよいでしょう。
PAゲージが0%のときの6ヒットの総合AA攻撃力について、各領域(PA≦9000、9000≦PA≦12000、12000≦PA≦16000、16000≦PA)の近似直線(AA計算式)を求めます。
まず、16000≦PAについては、実測値が6719.69≒6720。AA計算式=6720の定数と言ってさしつかえないでしょう。
12000≦PA≦16000では、PAが1000変わると実測値がほぼ60変化しています。傾きは60/1000=3/50と言えます。ここから切片は5760、近似直線は
AA計算式=3/50×PA+5760。
9000≦PA≦12000では、PAが1000変わると、実測値はほぼ80変化しています。傾きは80/1000=2/25、切片は5520、近似直線は
AA計算式=2/25×PA+5520。
PA≦9000ですが、PA8584とPA9000の二つだけでは範囲も500以内と狭く、いまいちよくわかりません。しかしながら、先ほど、B×PA+Cと傾向が同じだろうと述べました。これを利用してみましょう。Bの値がちょうど傾きと同じ意味ですからBを比べます。
12000≦PA≦16000では 1.0×10^(-6)。
9000≦PA≦12000では 2/15×10^(-5)で12000≦PA≦16000における数値の4/3倍。
PA≦9000では、2/45×10^(-5)で9000≦PA≦12000における数値の1/3倍。
AA計算式の方の傾きも、実は9000≦PA≦12000における数値(2/25)の1/3倍の2/75ではないか、という推測がなされます。
試しに2/75を代入してみると、切片は6000。2/75×PA+6000という式になります。これはPA8584、PA9000の両方について見たところ、実測値との大きな誤差はありません。この式で問題無いようです。
一方、Part6までの総合AA攻撃力の式は、
総合AA攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA]
でした。
ここで、0.12×PAを0にしてみた、
Z×{(Z-1)(B×PA+C)/2+0.30}×AA
を計算してみましょう。Z=6、AA=4000で、各PA領域でのBとCを用います。
「計算結果」とでもすると、

コピペではないです。まったく同じになりました。
これが6ヒット限定のものではないという一例として、PA15000について、PAゲージ0%での1~6ヒット全てについて軽く見てみましょう。計算ってついていないのは実測値から求めたもの、ついているのは計算して求めたもの。

最大誤差以内で一致します。
どうやらこの式で問題ないようです。PAゲージが0%のとき、
総合AA攻撃力=Z×{(Z-1)(B×PA+C)/2+0.30}×AA
0%のときに青式のようになったということは、PAゲージの割合によって、
今まで0.12×PAとしていた項が変化していると考えられます。
0%のときに0。100%のときに初期PAそのままが計算に関与するということは、
0.12×PA×PAゲージの割合
ではないか、という推測が出来ます。100%なら割合は1.00、50%なら0.50といったように。
この推測を裏付けるために、0%と100%の間の、何か特定のPA割合について調べてみると安心があります。0、1.00以外で分かりやすいポイントはPA再展開の瞬間(PAゲージの割合≒0.30)しかありません。これを調べましょう。
いったんPAを剥がしたあと、PAが再展開する瞬間にAAという手法です。どうしても人の手による関係で、PAが再展開してからAAが発動するまでの間にごくわずかながらPAが30%より多くなる→AA攻撃力が多少大きく評価されます。そのため、細かいことはさておき、0%と100%の攻撃力を結んだ直線上におおむね値が乗っていれば良いと考えます。要は、変な曲線にさえなっていなければいい。
各PA領域から1例ずつ測定(水色枠はPA値)。0%と100%は計算値で30%のだけ実測値。


直線上に乗っているようなのでとりあえず問題ないとみなします。体感で0.1~0.2秒ずれると20~40ぐらいの攻撃力の差が出ます。こだわる必要もないしそんなに頑張って測っていないです。ある程度の過大評価は構わない、過小評価が出なければとりあえずよい。
計算値は左からそれぞれ8083.05、8776、9900、10824です。
直線上に乗っていることが言えたので、単純な割合で計算できることがわかりました。
ということで、改めて、
段数=Z (1~6の整数値)、初期整波性能値=PA、AA攻撃力/OB=AAとして、初期PAによって値のとり方の異なる定数B、C、PAゲージの割合(0~1)を用いると、
アサルトアーマー攻撃力={(Z-1)(B×PA+C)+0.30}×AA+0.12×PA×PAゲージの割合
B×PA+C
=2/45×10^(-5)×PA-0.020 (PA≦9000)
or
=2/15×10^(-5)×PA-0.028 (9000≦PA≦12000)
or
=1.0×10^(-6)×PA-0.024 (12000≦PA≦16000)
or
=-8.0×10^(-3) (16000≦PA)
P-MARROW装備時はAA→AA×2.00になる(レギュ1.30現在)
多段ヒットの場合、
総合アサルトアーマー攻撃力=Z×[{(Z-1)(B×PA+C)/2+0.30}×AA+0.12×PA×PAゲージの割合]
ただし、ダメージが2倍になる現象等は未発生とし、水平面でのみ保証されるものとする。
PAゲージの割合≒(現在PA-初期PA×0.777)/(初期PA×0.223)より、
0.12×PA×PAゲージの割合≒0.12×(現在PA-初期PA×0.777)/0.223
に近似されるが、式が複雑になるため、普通に割合で考えた方がいいと思います。