Part0PA減衰量を調べるにあたっての方針とか。
Part1PA減衰量について大まかな傾向とか
Part2PA減衰量の距離減衰とか。
手間ヒマと誤差を考えるとPA減衰量について言えるのはここまででしょうか。
今回は、特定のPA減衰抵抗、PA整波性能でのPA減衰量の傾向を見ます。具体的には、PA減衰抵抗は100刻み、PA整波性能は1000刻みで、下限や上限に突入するならキリがいいところとかでやめ。
繰り返しになりますが、距離16程度という近距離かつ、PA減衰量は距離減衰前ならばパーツスペックに表示されているPA減衰力に比例することから、使用武器はTRESORのみ。条件は基本的にこれまでと一緒。
さっさと実測関連いきましょう。小数点以下も計算されていてグラフには反映されているけれど、下の表は列幅の関係で整数値のみ記載。表まわりの線は消すのめんどいのでそのまま。表の見方はPart1と同じです。
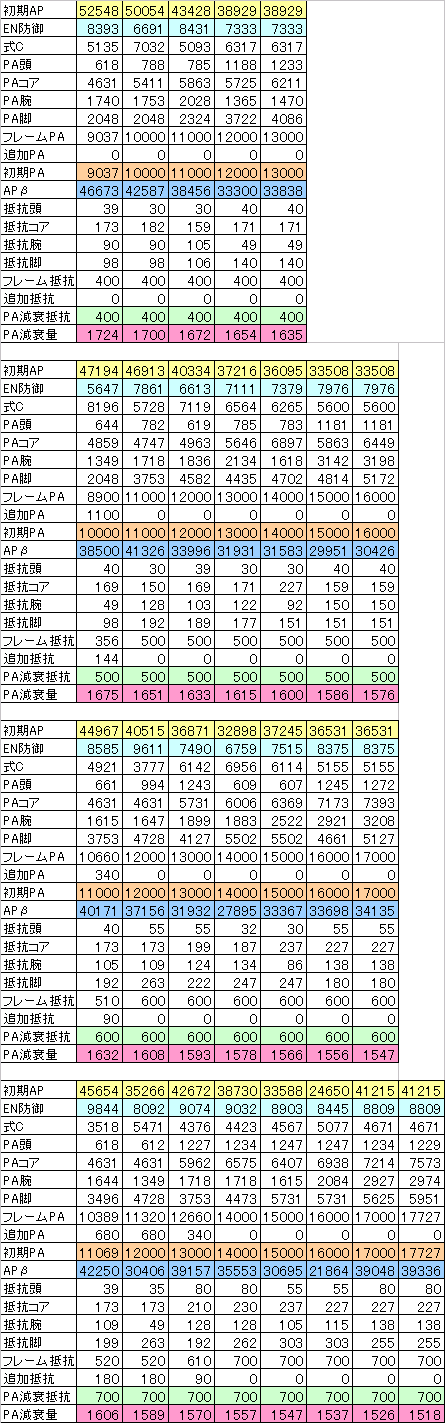
使用したフレームを知りたければ上記の数値を元に探してください。全部書くのめんどい。
測定用機体を作る時間>>Excel編集しつつ記事書く時間>>>>越えられない壁>>>測定時間っていう現実。
ちなみに、与ダメージが1変わるだけで、PA減衰量の値はおおむね4~8程度前後します。PA減衰量の測定誤差はそのぐらいあるものと考えてください。
PA減衰量部分のみ抜粋すると、
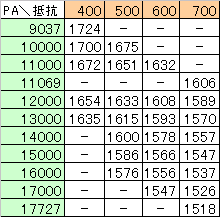
PA整波性能を横軸、PA減衰量を縦軸としてプロットしたものに近似曲線を書き入れると、
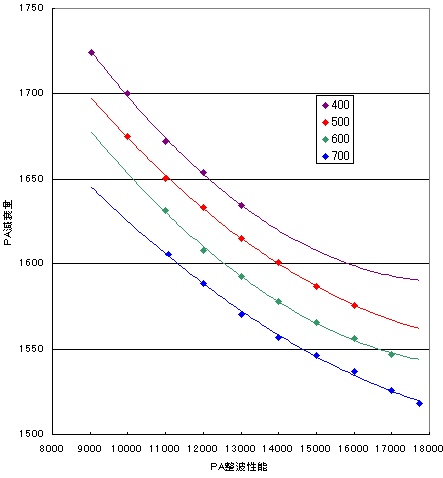
PA整波性能を変数とした場合、そのグラフは二次曲線に近似されると読み取れます。ただ、PA減衰量のプロット値がどれかひとつが少しでも変わるだけで(APβが1変わるだけで)二次曲線の式も結構動くので具体的にどういう式であるかって残念ながら断言できません。
近似曲線の一例として、PA減衰抵抗500についてのものを挙げると、
PA減衰量 =0.00000109×PA^2-0.04478974×PA+2013.06285434
R^2=0.99932283
になります。
少なくとも一次式では無いことは確定気味です。二次曲線の軸は、個人的予想では最大PA、あるいはそれ以上付近に来るとは思うのですがどうだろう?いろいろ試してみたけれど元データが安定していないから難しい。
別の視点で見てみましょう。PA減衰抵抗を横軸にした場合↓近似直線を作る際、3点以上プロット出来るPA整波性能値についてのみ記載。
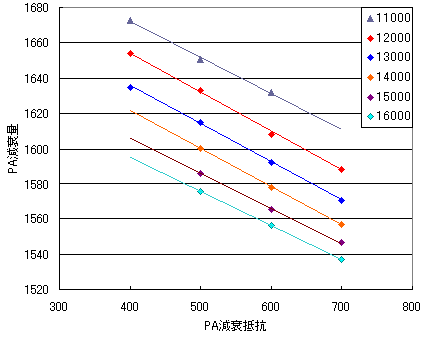
PA減衰抵抗を変数にした場合、どうやら傾きが同程度の一次直線になるようです。やはり測定誤差の大きさのせいで安定しなくてムカつく。傾きが同程度といっても誤差のせいでそれなりには値は異なるんだけれど、大丈夫だろうか。上の二次方曲線の方は二次係数がけっこう変動しているからもしかしたら一次直線じゃないかもしれない。怪しい。
---------------
以下単なる雑記。
PA10000以下の低PA領域等一部除いて誤差が6以内に収まり、なおかつ定数が比較的簡潔な式の例として、
PA減衰量=PA減衰力×1/4×{(-9/8×10^(-4)×PA減衰抵抗)+4/9×10^(-9)×(PA整波性能-22000)^2+8/9}
とかあります。これはよく分からない定数部分を勝手に決め付けたものであり、決して正確な式では無いですが、おおむねこれに類した式になると思います。
コジマチャージとかで、チャージ消費KPと同じKP出力に設定してPAが見かけ上増減しなくなるようにする手法も考えましたが、実際やってみるとチャージ開始時にほんのわずかですがPAが減少してしまって×。(肩のPA供給装置と時間差で合わせれば可能かも)
PA減衰抵抗とPA整波性能の両方を高めることで、相乗効果でPAが減衰しにくくなる上、PA整波性能そのものが高いと、PAゲージのPA量が増えるので(見かけの長さは変化しない)、PA消滅に至りにくくなる。JADOREとかEUPHORIAとか載せると効果的ってことだけれど整波装置のEN消費はいかがなるものか。パージ出来ないんだから低負荷でいいと思うんだけれど。バランスを間違えるといろいろ問題があるものの、一度は思い切って超高性能化されてもバチは当たらないと思います。
Part1PA減衰量について大まかな傾向とか
Part2PA減衰量の距離減衰とか。
手間ヒマと誤差を考えるとPA減衰量について言えるのはここまででしょうか。
今回は、特定のPA減衰抵抗、PA整波性能でのPA減衰量の傾向を見ます。具体的には、PA減衰抵抗は100刻み、PA整波性能は1000刻みで、下限や上限に突入するならキリがいいところとかでやめ。
繰り返しになりますが、距離16程度という近距離かつ、PA減衰量は距離減衰前ならばパーツスペックに表示されているPA減衰力に比例することから、使用武器はTRESORのみ。条件は基本的にこれまでと一緒。
さっさと実測関連いきましょう。小数点以下も計算されていてグラフには反映されているけれど、下の表は列幅の関係で整数値のみ記載。表まわりの線は消すのめんどいのでそのまま。表の見方はPart1と同じです。

使用したフレームを知りたければ上記の数値を元に探してください。全部書くのめんどい。
測定用機体を作る時間>>Excel編集しつつ記事書く時間>>>>越えられない壁>>>測定時間っていう現実。
ちなみに、与ダメージが1変わるだけで、PA減衰量の値はおおむね4~8程度前後します。PA減衰量の測定誤差はそのぐらいあるものと考えてください。
PA減衰量部分のみ抜粋すると、

PA整波性能を横軸、PA減衰量を縦軸としてプロットしたものに近似曲線を書き入れると、

PA整波性能を変数とした場合、そのグラフは二次曲線に近似されると読み取れます。ただ、PA減衰量のプロット値がどれかひとつが少しでも変わるだけで(APβが1変わるだけで)二次曲線の式も結構動くので具体的にどういう式であるかって残念ながら断言できません。
近似曲線の一例として、PA減衰抵抗500についてのものを挙げると、
PA減衰量 =0.00000109×PA^2-0.04478974×PA+2013.06285434
R^2=0.99932283
になります。
少なくとも一次式では無いことは確定気味です。二次曲線の軸は、個人的予想では最大PA、あるいはそれ以上付近に来るとは思うのですがどうだろう?いろいろ試してみたけれど元データが安定していないから難しい。
別の視点で見てみましょう。PA減衰抵抗を横軸にした場合↓近似直線を作る際、3点以上プロット出来るPA整波性能値についてのみ記載。

PA減衰抵抗を変数にした場合、どうやら傾きが同程度の一次直線になるようです。やはり測定誤差の大きさのせいで安定しなくてムカつく。傾きが同程度といっても誤差のせいでそれなりには値は異なるんだけれど、大丈夫だろうか。上の二次方曲線の方は二次係数がけっこう変動しているからもしかしたら一次直線じゃないかもしれない。怪しい。
---------------
以下単なる雑記。
PA10000以下の低PA領域等一部除いて誤差が6以内に収まり、なおかつ定数が比較的簡潔な式の例として、
PA減衰量=PA減衰力×1/4×{(-9/8×10^(-4)×PA減衰抵抗)+4/9×10^(-9)×(PA整波性能-22000)^2+8/9}
とかあります。これはよく分からない定数部分を勝手に決め付けたものであり、決して正確な式では無いですが、おおむねこれに類した式になると思います。
コジマチャージとかで、チャージ消費KPと同じKP出力に設定してPAが見かけ上増減しなくなるようにする手法も考えましたが、実際やってみるとチャージ開始時にほんのわずかですがPAが減少してしまって×。(肩のPA供給装置と時間差で合わせれば可能かも)
PA減衰抵抗とPA整波性能の両方を高めることで、相乗効果でPAが減衰しにくくなる上、PA整波性能そのものが高いと、PAゲージのPA量が増えるので(見かけの長さは変化しない)、PA消滅に至りにくくなる。JADOREとかEUPHORIAとか載せると効果的ってことだけれど整波装置のEN消費はいかがなるものか。パージ出来ないんだから低負荷でいいと思うんだけれど。バランスを間違えるといろいろ問題があるものの、一度は思い切って超高性能化されてもバチは当たらないと思います。
























