
おはようございます、こんにちは、こんばんは。ちみかなです。
次号の数独通信への投稿締め切りが10月末日だと知ってちょっとしょんぼりしています。
もっと先だと思ってました。まぁ、問題も作れていないので次々号に向けて、今からゆっくり
作っていきたいと思います。
さて、話はかわって。最近、疑問に思っていることが一つあるので、ここで吐露して、
あわよくば皆さんからご意見を伺いたいな、と……。
ゲーム理論の初歩でよく出てくるお話に、「海賊と金貨の問題」というのがあります。
問題は以下のようなもの。(問題はここから引用)
5人の海賊が戦利品の金貨100枚を山分けすることになりました。この海賊たちには
親分から下っぱまで身分の違いがあって、山分けにあたって次のようなルールがありま
す。
まず親分が5人それぞれの取り分を提案します。全員の多数決で少なくとも半数以上の
賛成があればその提案のとおりに山分けがされますが、賛成が半数に満たなければ、そ
の提案者(親分)はその場で殺されて同じことのやり直しとなります。(親分が殺され
た場合は次はNo.2が提案をすることになります)
こうして山分けの案がまとまるまでこのルールは繰り返されます。さて親分であるあな
たはどのような山分け案を提案したらよいでしょうか。
もちろん、海賊同士は相談や共謀をすることはできませんし、皆、論理的かつ貪欲で誰
も死にたくないと思っています。
=引用ココマデ=
明文はされていませんが、
身分の低い者は、
現提案者の山分け案でもらえる取り分>それ以降にもらえそうな取り分:賛成
現提案者の山分け案でもらえる取り分≦それ以降にもらえそうな取り分:反対
と判断するものします。
一般的には以下のように考えることで、解答を得ます。
=解答=
身分の高いほうからA,B,C,D,Eとする。
まず、なんらかの理由によりA~Cの山分け案が否決され、D,Eだけが残った場合を考
える。このとき、D:E=100:0という山分け案を提案すれば、Eは反対するであろうが、
D自身は賛成するため、この案は必ず可決される。よってD,Eが残れば、必ずD:E=100:0
という提案が可決する。
C,D,Eについて考える。Cが山分け案を提示するため、Cを除くとDかEのうち一人が
賛成にまわればよい。ところでそれぞれを賛成させるには上記より、Dならば101枚
以上、Eならば1枚以上のコインを分け与える必要がある。Cは金に貪欲であるため、
分け与えるコインが少なくてすむように動く。つまり、Eに対して(最小限で賛成にまわ
る)1枚を与える。Dには反対されてもよく、反対の者に分け前を与える必要もないの
で0枚でよい。
よって、C:D:E = 99:0:1
B,C,D,Eについて考える。Bの山分け案が可決されるには、C,D,Eのうち一人が賛成に
まわらなければならない。同様にして考えると、賛成にまわる最低金額はCが100枚、
Dが1枚、Eが2枚である。この中ではDを賛成にまわらせるのが、もっともBにとって
支出が少なくてすむ。よってB:C:D:E=99:0:1:0
では、Aの場合の山分け案について考える。5人のうち半数以上の賛成を得るには3人の
賛成が必要である。提案者のAは賛成にまわるとして、残り2人。前述と同様に考え
るとBは100枚、Cは1枚、Dは2枚、Eは1枚で賛成にまわる。
ゆえに、A:B:C:D:E=98:0:1:0:1 という山分け案を提案すればよい。A,C,Eは賛成し、
B,Dが反対することで可決されるはずである。
=解答ココマデ=
最初きいたときは、そんな馬鹿な、と思いました。なんだかAが得をしすぎている気がし
て。でも、反論できない。だから、納得してきました。やがて、時がたち、これが正解なん
だと思ってきました。
ただ、最近、ふと疑問に思ったんです。
果たして、こんな状況は起こりえるのだろうかと。
上記の説明は獲得硬貨枚数が3枚以上ならば何枚であっても成り立ちます。つまり、B~Eの
取り分はコインの枚数の多少にかかわらず0枚か1枚なんです。
そして、海賊メンバーは全員「論理的」な思考ができるので、自分の取り分が0枚/1枚であ
ることをB~Eは舟を襲う前には知っています。
海賊行為によって捕まるかもしれない、逆襲にあって殺されるかもしれない、よしんば獲物
が得られても自分の取り分は0枚/1枚……。
「貪欲」で「死にたくない」と思っているはずのB~Eが海賊行為に参加するのは論理的行動
でしょうか。
そういった理由で「5人の海賊が戦利品の金貨100枚」を得ること自体が矛盾しているように
思います。
勿論、「貪欲であるけどそれ以上にこの海賊に対する愛が深かったんだよ」みたいな反論は
あるかもしれません。ただ、そういった文言は問題文に書かれていません。
こういった場合、問題文に書いてあることを事実として受け止め、解答にあるような答をす
るのがいいんでしょうか。
自分はそこらへん、詳しくないのでよく分かりません。
……とか、書いているうちにもう2時過ぎ!? もう寝なきゃ。お、おやすみなさいー(汗
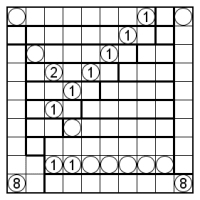
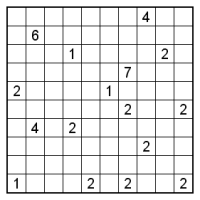
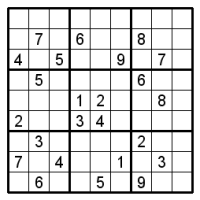
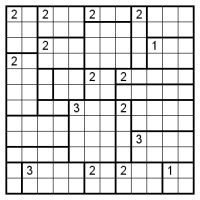
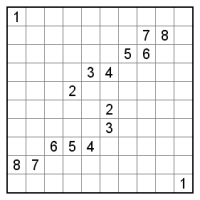
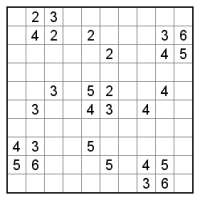
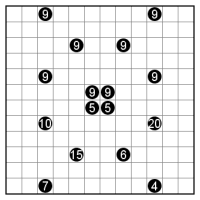
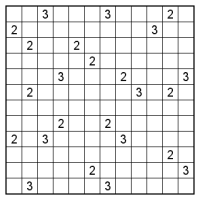
さて、画像はひとりにしてくれです。カンペンはこちら。
次号の数独通信への投稿締め切りが10月末日だと知ってちょっとしょんぼりしています。
もっと先だと思ってました。まぁ、問題も作れていないので次々号に向けて、今からゆっくり
作っていきたいと思います。
さて、話はかわって。最近、疑問に思っていることが一つあるので、ここで吐露して、
あわよくば皆さんからご意見を伺いたいな、と……。
ゲーム理論の初歩でよく出てくるお話に、「海賊と金貨の問題」というのがあります。
問題は以下のようなもの。(問題はここから引用)
5人の海賊が戦利品の金貨100枚を山分けすることになりました。この海賊たちには
親分から下っぱまで身分の違いがあって、山分けにあたって次のようなルールがありま
す。
まず親分が5人それぞれの取り分を提案します。全員の多数決で少なくとも半数以上の
賛成があればその提案のとおりに山分けがされますが、賛成が半数に満たなければ、そ
の提案者(親分)はその場で殺されて同じことのやり直しとなります。(親分が殺され
た場合は次はNo.2が提案をすることになります)
こうして山分けの案がまとまるまでこのルールは繰り返されます。さて親分であるあな
たはどのような山分け案を提案したらよいでしょうか。
もちろん、海賊同士は相談や共謀をすることはできませんし、皆、論理的かつ貪欲で誰
も死にたくないと思っています。
=引用ココマデ=
明文はされていませんが、
身分の低い者は、
現提案者の山分け案でもらえる取り分>それ以降にもらえそうな取り分:賛成
現提案者の山分け案でもらえる取り分≦それ以降にもらえそうな取り分:反対
と判断するものします。
一般的には以下のように考えることで、解答を得ます。
=解答=
身分の高いほうからA,B,C,D,Eとする。
まず、なんらかの理由によりA~Cの山分け案が否決され、D,Eだけが残った場合を考
える。このとき、D:E=100:0という山分け案を提案すれば、Eは反対するであろうが、
D自身は賛成するため、この案は必ず可決される。よってD,Eが残れば、必ずD:E=100:0
という提案が可決する。
C,D,Eについて考える。Cが山分け案を提示するため、Cを除くとDかEのうち一人が
賛成にまわればよい。ところでそれぞれを賛成させるには上記より、Dならば101枚
以上、Eならば1枚以上のコインを分け与える必要がある。Cは金に貪欲であるため、
分け与えるコインが少なくてすむように動く。つまり、Eに対して(最小限で賛成にまわ
る)1枚を与える。Dには反対されてもよく、反対の者に分け前を与える必要もないの
で0枚でよい。
よって、C:D:E = 99:0:1
B,C,D,Eについて考える。Bの山分け案が可決されるには、C,D,Eのうち一人が賛成に
まわらなければならない。同様にして考えると、賛成にまわる最低金額はCが100枚、
Dが1枚、Eが2枚である。この中ではDを賛成にまわらせるのが、もっともBにとって
支出が少なくてすむ。よってB:C:D:E=99:0:1:0
では、Aの場合の山分け案について考える。5人のうち半数以上の賛成を得るには3人の
賛成が必要である。提案者のAは賛成にまわるとして、残り2人。前述と同様に考え
るとBは100枚、Cは1枚、Dは2枚、Eは1枚で賛成にまわる。
ゆえに、A:B:C:D:E=98:0:1:0:1 という山分け案を提案すればよい。A,C,Eは賛成し、
B,Dが反対することで可決されるはずである。
=解答ココマデ=
最初きいたときは、そんな馬鹿な、と思いました。なんだかAが得をしすぎている気がし
て。でも、反論できない。だから、納得してきました。やがて、時がたち、これが正解なん
だと思ってきました。
ただ、最近、ふと疑問に思ったんです。
果たして、こんな状況は起こりえるのだろうかと。
上記の説明は獲得硬貨枚数が3枚以上ならば何枚であっても成り立ちます。つまり、B~Eの
取り分はコインの枚数の多少にかかわらず0枚か1枚なんです。
そして、海賊メンバーは全員「論理的」な思考ができるので、自分の取り分が0枚/1枚であ
ることをB~Eは舟を襲う前には知っています。
海賊行為によって捕まるかもしれない、逆襲にあって殺されるかもしれない、よしんば獲物
が得られても自分の取り分は0枚/1枚……。
「貪欲」で「死にたくない」と思っているはずのB~Eが海賊行為に参加するのは論理的行動
でしょうか。
そういった理由で「5人の海賊が戦利品の金貨100枚」を得ること自体が矛盾しているように
思います。
勿論、「貪欲であるけどそれ以上にこの海賊に対する愛が深かったんだよ」みたいな反論は
あるかもしれません。ただ、そういった文言は問題文に書かれていません。
こういった場合、問題文に書いてあることを事実として受け止め、解答にあるような答をす
るのがいいんでしょうか。
自分はそこらへん、詳しくないのでよく分かりません。
……とか、書いているうちにもう2時過ぎ!? もう寝なきゃ。お、おやすみなさいー(汗
さて、画像はひとりにしてくれです。カンペンはこちら。












※コメント投稿者のブログIDはブログ作成者のみに通知されます