数学って何だ・・・・・数学における美意識と有用性・・・・・

Photo: Kashiharajingū-mae Station


本文は数学に馴染みのない人向けのおさらいです。一方加筆した部分では、数学者でも多くの方が意識していない、よりクリエイティブな面に触れています。

１．算数から数学へ


ちょっと数学についておさらいします。
◎数量分野：数と代数
　小学の算数では数とその四則演算を学びます。中学数学で著しいのは、数の代わりに文字を使うことです。たとえば

ab+ac+ad ＝ a(b+c+d)

を知っていると、a, b, cがとても大きい数であるとき掛け算の多い左辺よりも右辺のほうが早く計算できるでしょう。でも文字導入の効用は、そんな効率的な公式の暗記に便利というようなことにとどまりません。一つは、未知の数 x を既知の量のように扱うことによって、その持っている性質を導き、そこから x の候補を絞ってゆくという方程式の手法です。２倍して３を引くと5になる数は何かというような問題です。2x－3 ＝ 5 と方程式を書けばあまり考えないで済みます。
さらに数学というのは数という対象をさらに進めて、例えば

ab+ac+ad ＝ a(b+c+d), 　　ab ＝ ba

のような形式そのものに興味を移します。個別の数を扱う算数から、一般化された数である文字とそれに加える操作の法則が数学の対象となるのです。今の場合は法則は分配則と交換則です。このような数に適用する演算法則を抽象して代数学が出来上がります。
数学は算数が何をやっているかを考えるメタ算数なのです。だから 1+1 ＝ 0 となる算数から見れば外道の数学さえあります。これは偶数０を奇数を１と読めばよいのです。四則演算ができる「数」のようなものが出来ます。同様に 1+1+1 ＝ 0 となる数学もあります。

ならび飛ぶ蛾の一群の増えゆきて頬を掠める翅音ベウベウ

◎図形分野：幾何学
図形分野の方では、長さや面積、体積の公式が実用上重要です。これも、早くから一般化された公式が発達しました。図形はとてもとっつきやすいのですが、一般化された結果を納得するには、それが普遍的に成立することを証明せねばなりません。まず概念を抽象して表わし、論理を用いて示すのです。
論理とは、仮に「阪神ファンはみな納豆がキライ」が正しいとしても、「納豆がキライな奴はみな阪神ファンや」ということは出てこないといったことです。もう少し数学らしい例で言うと「正四面体は４つの面積の比が1：1：1：1である」が「４つの面積の比が1：1：1：1の四面体は正四面体であるか」というのは正しいでしょうか。これはうっかりすると正しいように見えますが、次の図に見るように、そうではありません。これらは逆命題は必ずしも正しくないという例です。あたりまえのことですが、日常の込み入った議論をよく見るとこんなおかしな理屈を用いてることがしばしばあります。(＊)




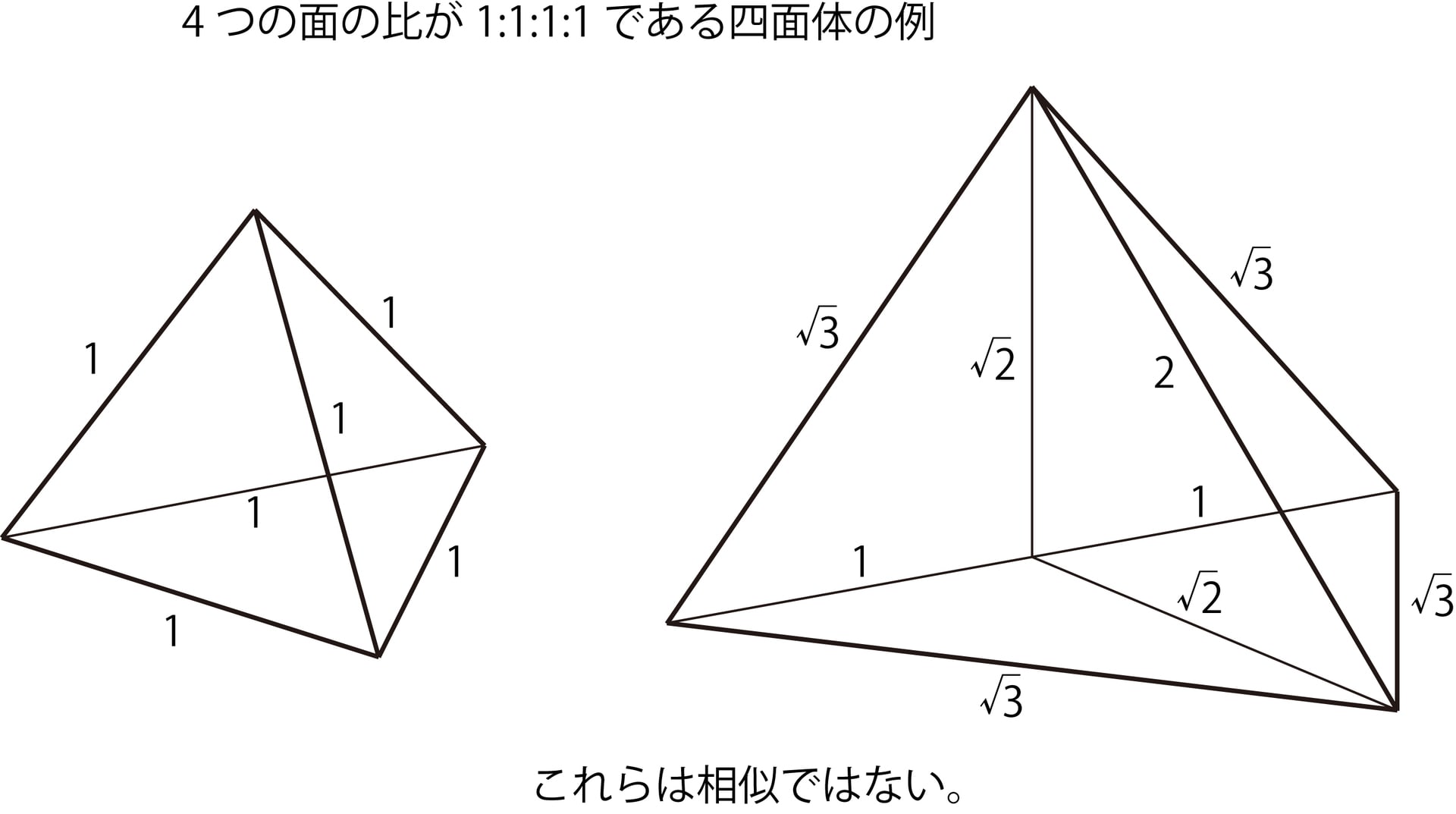
ユークリッド幾何の完全な解答を練習していると、何を前提とするか、そこからどういう推論が許されるかということに敏感にならざるを得ません。数学は論理学と不離のものといえます。
それと反対のようなことですが、図形は直感力を必要とします。空間感覚と呼ばれます。例えばいい補助線を見つけるというようなこと。ある程度生まれつきの才能です。幾何学的審美眼は導きの糸で「いい数学」を教えてくれます。またこれがないと、人にそれが良い結果であるという感覚を呼び起こさないのです。

外套のポケットの内へと身を投じ世界を捩じるクライン・ボトル

◎無限の分野：解析学　高校数学で劇的に登場するものは微分、積分です。まず変数 x にいろいろな値を取らせて変化させるとき、それに応じて変化する数 y を考え、これを x の関数と言います。xy 平面にグラフで表わされるものです。一般に x や y は無限個の値を取ります。微分とは x がある値の近くでちょっと動くとき y がその何倍動くかという比、つまりグラフの勾配のことです。ニュートンやライプニッツが物の運動を表現するために考えだしたものです。かくして初期には、微分学、積分学はニュートンの力学と不離のものでした。しかし今の高校では、「入試範囲」の関係でできるだけ分離されています。とても不自然です。

光河より Harley-Davidson 流し来る頭蓋にあおき萍つけて



２．数学の有用性


曽野綾子に次のような有名な言葉があります。中学教科書において必修とされていた２次方程式の解の公式を指して、作家である自分は「二次方程式を解かなくても生きてこられた」「二次方程式などは社会へ出て何の役にも立たないので、このようなものは追放すべきだ」（この後、夫・三浦朱門が教育課程審議会で削除を主張し、中学課程で「二次方程式の解の公式」は必修事項から削られたのです。今は復活しているようです。）たしかに店頭の計算や家計簿のレベルでは、２次方程式もピタゴラスの定理も要りません。実用の範囲を述べているのです。
しかしこの公式を「平方完成」を通じて導くことは、数学の面白さへのとても良い入り口と思います。曽野さんは「学校教育の場では『日の丸』を掲揚し、『君が代』をきちんと歌わせる」べしとも述べているから、実用に徹しているわけではありません。任せておくと『君が代』を歌わないと生きていけないという処世術が流行るようになるかもしれません。
次は２次方程式よりはるかに厄介な５次方程式の話です。

x⁵ + 3x³ - 2x + 6 ＝ 0

のようなものです。エヴァリスト・ガロアは一般の５次方程式にたいしては「四則演算と累乗根を取る有限回の操作では根は表せない」というアーベル--ルフィニの定理の証明の簡略化のために群論を創出したのです。つまり群論は非常に純粋に理論的な動機で生まれたのです。群論は代数学のうちで構造としてはもっとも基本的なものです。もっとも単純だからもっとも一般的なものです。
群はのちのレヴィ・ストロースの文化人類学的考察に登場した「構造」で、構造主義流行の出発点と言われています。オーストラリアのカリエラ族は4つのグループに分かれていて、子供が何処に属するかという規則と、婚姻規則を併せるとクラインの４元群が現れてくる。それが自然にインセスト・タブーに合致しているというような説です。この４元群とは1, i, j, k の４個の元からなり、次の法則を満たす積×が定義されたものです。

1×i ＝ i×1 ＝ i, 　　1×j ＝ j×1 ＝ j, 　　1×k ＝ k×1 ＝ k,
　　i×i ＝ 1, 　　　j×j ＝ 1,　　　k×k ＝ 1,
i×j ＝ j×i ＝ k,　　 j×k ＝ k×j ＝ i, 　　k×i ＝ i×k ＝ j 　

これぐらいでは、理論ではあっても、あまり実用的ではない話と思われるかもしれません。しかしいまや群論は計算機科学や理論物理の基本的な言語となっています。
群論に限らなければ、科学と名のつくもので数学を用いないものを挙げることが困難でしょう。たとえば、僕の若かった頃は生物の分類なんてものは、素朴な形態学で、数学から非常に遠く見えましたが、今や分子系統学と言って高度の数理的な解析が行われているようです。有用性は枚挙に暇がありません。また先程述べた論理性を身につけると、いろいろな場面で無駄が無くなるでしょう。数学の成果は世の中を覆っています。数学は役に立たないと言いながら、メールを使ったり電車に乗っているのは罰当たりなことです。言われるほど無用なものではないのです。
そういう有用性を認めると、数学を生業とするものの間では、数学の中での有用性というものも生じます。他の数学の進展に役立つということです。さらに数学を用いる人間を育てるためにも、数学を学び伝承する必要が生じます。２次的必要性です。
といっても、むろん人には持ち場というものがありますし、文明不要という立場もありますから、全員に数学を学べと言うつもりはありません。
ただ、「この売場で1億円のアタリが出たから、ここで買おう」なんて言い草は、数学的に言えば「ここで大きなアタリが出たから、ここではもうアタラン」というのと同程度に、非合理なのです。でも人によっては験を担いで安心を得るということはのこるでしょう。実は僕自身も験を担ぐこと皆無とはいえません。例えば幾本か並んだ柱の間を通って入りまた出るとき、同じところを通って軌跡が柱に絡まないようにするほうが気分がいいとか。
数学はどの科学に比べても一番間違いのないものです。というよりも、間違いのない推論を集めたものです。一段一段本当に当たり前のことで成り立っているのです。それが積み重なると解らないものになる、0と1を並べた計算機のやることも似たことです。

葦の州に伏したる身より羽化を遂げ沖に渦なす群れに向へり
　　　　　


３．数学における美


数学は実用を目指してるのか、と言われると多数の数学者は否と応えるでしょう。学者にかぎらず、数学を好む人はある種の審美眼を持っています。「直角三角形の直角を挟む２辺の長さの２乗の和は斜辺の長さの２乗に等しい」というピタゴラスの定理を見たとき、美しいと感じるでしょう。自分でそんなものを発見したいと思います。朔太郎や谷川俊太郎のような詩を書きたいと思うのと変わりません。世の中に認められたいという野心もあるでしょう。
どんな数学が美しいのでしょうか。数学を生業（なりわい）とする者の間でよく賞賛されるのは、まったく論理的でなくこれ自体美的でもありませんが、列挙してみると次のようなことがあるでしょう。
◎一般的である。その理論がいろいろなところに適用できるということです。このために数学者は必要な条件をできるだけ減らし、結論が成立する範囲を増やそうとします。
◎簡潔である。上のピタゴラスの定理などは申し分のない短さで、しかも整った感じを受けます。これも前提条件が少ないから一般的であるということになります。
◎飛躍がある。結果が必要な条件から想像しにくいことであれば感激します。そしてそこから引き出されるものも多くなります。代数学と解析学と幾何学をいっぺんに結びつけるような定理が素晴らしいのです。
ただし論証には、飛躍があってはならないことが大切です。一見とても素晴らしい発見が、論理に飛躍があって取り下げられることはしょっちゅうあります。数学には間違いがないといいましたが、新しい数学理論を作る手前で誤りがいくつも生起します。僕の習った溝畑先生の言葉に「よく間違えるときが一番前進しているときです」というのがあります。
僕は完成した後も、夜中に「しまった」と言って目をさますことが何度かありました。１０年も前に成し遂げて論文にしたことに誤りがあったと気がついたからです。飛び起きてチェックするとたいてい思い過ごしであることが判明します。論文作成中はよく見えているから存外うまくやっているのです。小さな傷が残っていることはあります。たまには大きな傷も。傷があってもあまり指摘されず通用していることさえあると聞きます。

しかし美をむやみに敷衍して神秘化するのも困ったことです。僕が数学者と知ると、しばしば岡潔さんの言う「情緒」について同意を求められます。面白いことにそういうことを言うのはほとんど数学を扱わない文学的な人が多いのですが。「情緒とは感情や感覚と異なるもので、日本人が特に持っているもの」と言われているそうです。情緒を解することは結構ですが、一律に外国人に優位を感じたり、ものをはっきりいう人に情緒がないと言うのは賛成ではありません。アンチ・ラディカリズムの標語にもなっている気がします。特に数学の新しい装置は、しばしばドライに見え、それまでの手作り的な方法の方が情緒があって良いと言う感じがするのです。しかしその新しい道具に慣れてくると、その方が自然になってくることが多いのです。新しい方法とは、例えば縦横に並べられた柿を、端から数えるのではなく、縦かける横の掛け算で計算するようなものです。でも僕が新しい道具に強いというわけではなく、むしろ逆なのですが。

しかし、僕も岡さんの数学そのものには恩恵を受け、画期的なものだと思っています。難攻不落であった多変数関数論、ひいては代数幾何学を動かす数歩を進めた人です。「不定域イデアル」というアイデアが大切だったのですが、これを用いる議論はかなり煩雑でした。メモリーが小さい頭には収まりきりません。Henri Cartan,　Hans Grauert,　Reinhold Remmert や、トポロジストの「層」による綺麗な整理を得て、やっと頭に入るようになったのでした。
しかしこの層というものでも、抽象的で厄介です。上の柿を数える例で言えば九九を憶えるような努力が要ります。しかし覚えた後は幾何学化され安定した便利な概念となります。だから僕はこの「層の概念には情緒がない」などと言うべきではないと思っています。その層が岡さんの不定域イデアルという画期的で飛躍した概念から始まったことも事実です。
数学において美は重要で、しばしば導きの糸となります。しかしそれは、個性や、段階により変わるものです。どちらかと言うと格好構わずのたうち回るうちに掴むものであり、あまりアプリオリに目標とすべきものではないと思います。
岡さん自身においても、その修羅の一端が下のコメントで引いた動画からうかがえると思います。

創造というものは飛躍した発想がいるものです。考えの幅が広いことがその飛躍を助ける面はあると思います。その「教養」を情緒という言葉でくくることは無理です。ぶっ飛んだ発想をする僕の友人の場合、その能力は頻発するダジャレと関係があるように見えます。また「考えの幅」にはガロアの「革命」さえも含めるべきです。

茄子紺の海を吊るせる綱一本うねり高まる沖つ海坂
　　　　　


４．数学研究の可能性（僕の経験から）


僕が２０才の頃、数学史で高名なK先生の授業で、数学は「若い才能が大切である。２０歳になって何かの結果を出していないようでは絶望だ」という話を聞いたことがあります。嫌な気分でしたが、僕は執着を変えられませんでした。後年、大学で同級であり、数理生物学に進んで成果を上げ、さる大学の副学長まで勤めた女性の友人がいました。あるとき彼女に「数学に進んだ人たちは自信が強いね。K先生のあんな話を聞いていながら。私は諦めた。」と言われました。それでも数学の多くの友人は、K先生の話とうらはらにどんどん仕事を仕上げていきました。

しかし僕はそうは行きませんでした。数学で何かの新しい命題を得ようとするなら、ある程度今の水準を知らねばなりません。理論展開を独力でやろうとすれば、最低でも歴史が要したのと同じ時間がかかってしまいます。だから先行する人の仕事を用いるのです。でもその主張を読み解くだけでも時間がかかります。活用するためにはその意味を深く理解しなければならないからです。しかし調べようとして手にした論文の参考文献を見ると、その数が１００を超えることもあります。その一つを取るとまた多くの論文が用いられています。強烈なねずみ算です。若いころはそれを見て絶望的になりました。指導教授に研究を止めるように勧告を受け、４０才を過ぎるまでまともな結果を出せず、不甲斐なさにつらい思いをしました。K先生の言われるように絶望でした。

一つ大切なことは、良い問題を掴むことです。通常は指導教授に頂くのですが、僕は記憶力が極端に無く学習能力も低くて、課題をこなせなかったのです。それでも僕のモラトリアム性もあって、大学におり続け、「関数の位数」という自分にわかる素朴なものにしがみついていました。関係ありそうな話を求めて、よく分からぬ代数幾何学という分野の話も聞きに出掛けました。そこで当時の院生、泊正孝さんの話を聞いて、それまで１０年ほど考えて絶望的になっていた問題の解き方が閃いたのです。それを元に新しい理論を構築して一挙に視野が開けました。セレンディピティです。つまり探し求めて苦労していると、思いがけないチャンスがつかめることがある、ということです。４０代に入っていました。大学に居続けられたのは、時代が許した幸運です。
このときもう一つ気がついたことがあります。実は先人の仕事を全部完全にチェックしなくてもよいということです。広中平祐さんの特異点解消の論文は電話帳と呼ばれる分厚いものです。とても広範な応用があるのですが、元の論文を証明まで理解して用いている人は少ないと思います。僕も証明を読み通さず度々用いています。独自の問題意識を持ち、幾つかの良い論文を踏破しておけば、他の論文をある程度見極める力がつくのではないかと思います。この要領を掴まなければ、学習能力の低い僕は泥沼から抜け出せなかったでしょう。
随分前のことですが、岡潔さんが「現代の数学は勉強することが多くなっているから４０代ぐらいにならんと成果は挙げられない」といった趣旨の発言をされたそうです。まったくそう思います。しかしいまは大学院で幾つかの論文を書くくらいでないと研究職に残れないでしょう。K先生の言われたことに近づいた恐ろしい時代です。

よく「数学にはいまでも新しい発見があるのか」という質問を受けます。むろん、数学自身にはいくらでも可能性が残っていて、雑誌は新しい結果を得た投稿者で溢れかえっているほどです。また数学者はまだ人工知能にも負けていません。
しかし手っ取り早い研究では結果も浅くなるでしょう。現役教員は教育と宣伝、書類作成でとても忙しいのです。良い研究がアマチュアや退職者からも出る時代が来るかもしれません。先端文献はネットで取れるし、あと必要なものは本と計算機ぐらいです。いちばん大切なのは暇だと思うのです。でももう一つ、できればほしいものがあります。人の交流を保証する旅費です。これは職についてないといただけません。

ところで一つの理論を取り上げて、実際的なことに役立つかと言えば、先程も申し上げたように、大方の数学研究者は「実用を目指しているのではないのでわからない」と言うでしょう。これまでの数学を取り巻く歴史と自分の経験を見ていると、好きなことをやっているからこそ、予想外の応用も生まれてくる可能性もあると感じるのです。これは理学というものの性格で、ノーベル賞の大隅さんの言われることもそんなことだと思います。僕は自分のやったことはいつか役に立つかもしれない。しかしそんな日が来るより早く人類が滅びているかもしれないというような気持ちでやっています。

高層の窓に依りたる身体が分子になってほどけているよ　　




(*) (2016/12/26 加筆)
論理性は数学を語るとき定番の言葉である。なぜなら数学は演繹的な論理そのものといえるものだからだ。数学を理解し、用いる場面では正しい推論は決定的に大切である。しかしこれは数学の面白さを言い得てはいないと感じる。この退屈さはなぜだろうと考えていた。

最近 Facebook の垂水源之助氏の記事で「アブダクション (abduction)」と言う語を教えていただいた。
「土が湿っている。雨がふると、土が湿る。つまり雨が降ったに違いない」
というような推論であるという。パース (C.S.Peirce)が考え出し強調したと言う。推論には演繹、帰納、アブダクションの３種があるというのである。理論を作り出す場面ではアブダクションがもっとも働くという。われわれ一般の数学者はアブダクションを用いながらも、この概念を意識していないのだろう。

この推論はもっともクリエイティブであるが、もっとも誤りを導くものでもある。「前へ進むとき、誤りが頻発する」という溝畑先生の言葉はこういう文脈で了解される。しかし裁判でアブダクションだけを用いれば冤罪が頻発するであろう。数学においてもアブダクションで掴んだ事柄は、必ず論理的に証明しなければならないこと、言うまでもない。

要するに、このアブダクションという概念は、僕の話題を結びつけ、ある種の退屈さから救ってくれもののようだ。詳しくは次の書にある。未読であるが、ポリアの発見的推論ももう一歩進めればアブダクションに到達するという。
米盛裕二著　勁草書房, 2007, ISBN 978-4-326-15393-0　３０２４円

--------------------------------------------------
北村虻曳: 神戸を中心とする詩人グループ「Melange」での談話(2016/11/20)に加筆
短歌は北村の旧作

Melangeの方から要望がありましたので、上の話に関連する書物、動画を下にコメントとして挙げておきます。