簡単な図式解法
算数の計算の殆どは、簡単な図式解法があります。数学的に高度に考えない方法として、小学生にも解りやすい計算法です。
ピタゴラスの定理も殆どの皆様が、直角三角形の各辺に対応した正方形の面積として、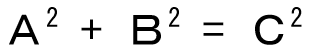
の式で学んだと思います。
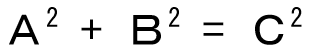の式で学んだと思います。ここに解説している暗算法も、同様に２つの数字の掛け算も以下のように図で計算する方法（面積式・直線式）があります。
23 × 45 という２桁の掛け算について説明してみましょう。
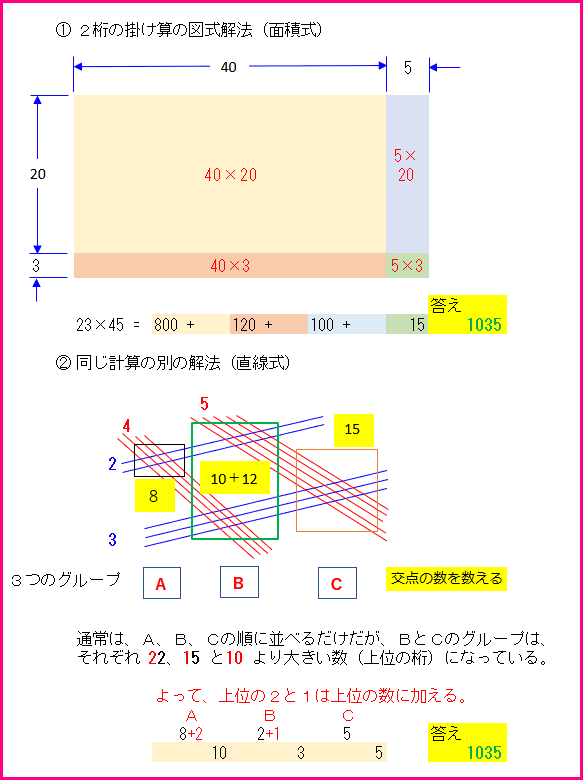
直線式で計算する場合、この図では数だけ合わせたいい加減な直線を
引いていますが、実際には、対角線を結んだ線が直交する横長の◇型
になるように作図した方が、上下の位置関係（位取り）を間違わずに
計算することができます。必ず左側、上側が上位の数字を示します。
× 11 の計算法の続き
昨日学んだように、最下位と最上位の数字は基本的に不変です。が、最上位の数字と中間の数字は、直線式解法からも解るように隣接する2つの数字の和が10を超える場合、10なら１、20なら２･･･と上位に繰り上がります。
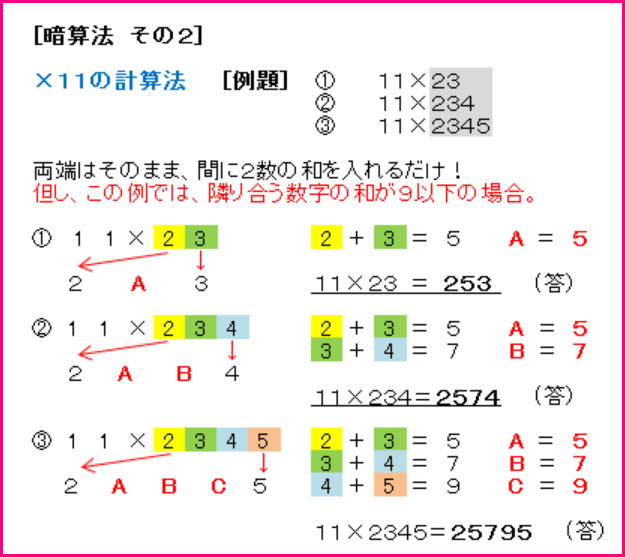
同じ計算を直線式で解いてみてください。繰り上がりが無いのでより簡単ですね。以下の例（その３）は、隣接する2つの数字の和が 10 を超える（繰り上げが必要）例です。
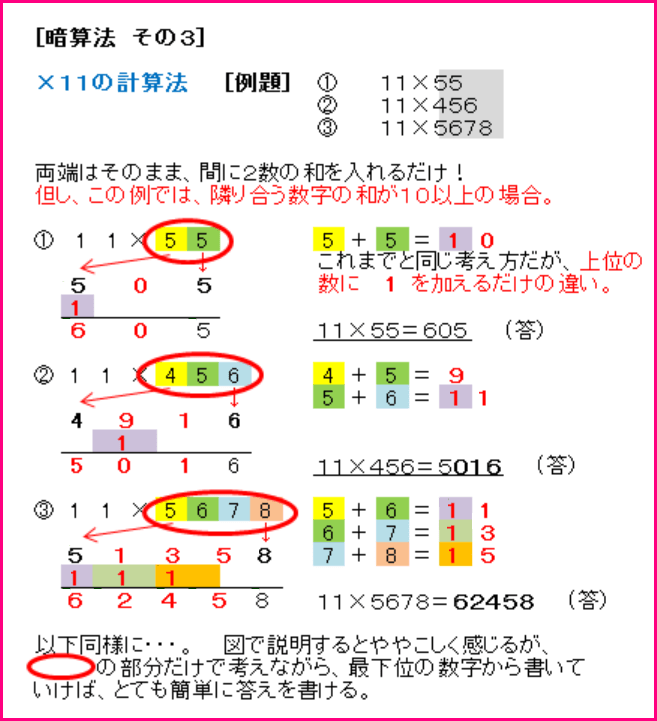
昨日も書きましたが、答えは上位側からでも下位側からでも構いませんが、基本的には隣接する数字の和が「９」以下であれば上位から、それ以外は下位側から書いた方が間違いが少ないです。（予期せぬ繰り上がりがあるため）
このシリーズは10回以上続きます。
どれか一つ覚えておくだけでとても役に立ちます。
本日もご来訪いただきありがとうございました。
スマホでどうぞ 
暗算の仕組みはそうなっているのですね。
説明されると理解できるのですが、私などは暗算のできる人を超能力者のように思っていました。
あらためて「う～ん」「う～ん」と頷く自分に気づきました。
いつもご訪問・コメントをありがとうございます。
暗算の手法も特技の一つとして、数ある中からどれか一つだけでも知っていることで、人生のいろんな場で役立つことが多いで、ご活用ください。
話題が尽きたとき、余興の一つとしてするとき、子供を良い意味で驚かせるときなど、活用の場は様々です。
「何もいい年をしてこんなことを覚えなくても･･･」という方もおられるでしょう。
でも、「知識」はいくら知っていても管理費がかかる訳ではなく、知っているだけその人が得をすることが多いものです。