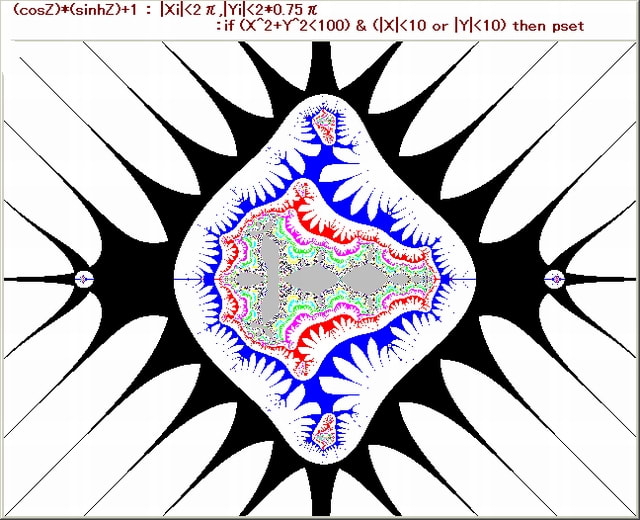
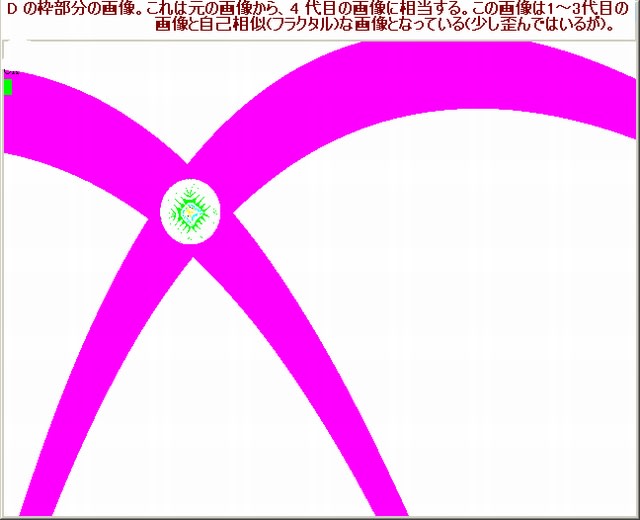
前記事の、ひ孫1画像の”噴煙”部分は、どうなっているのか?
それを調べるために、今回は、ひ孫1画像の”噴煙”部分の一部を拡大してみる。
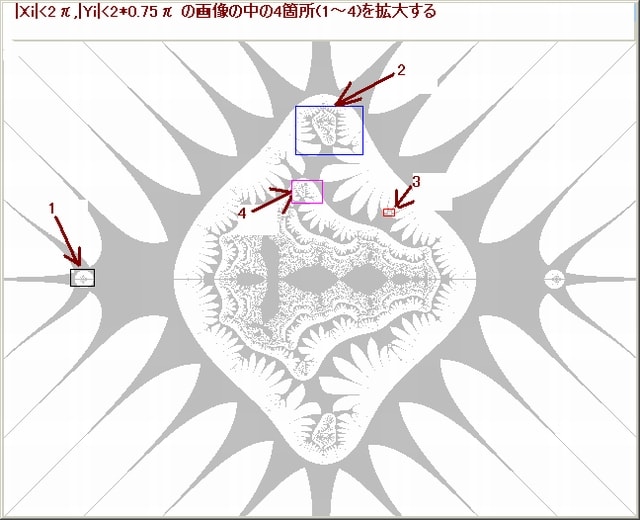
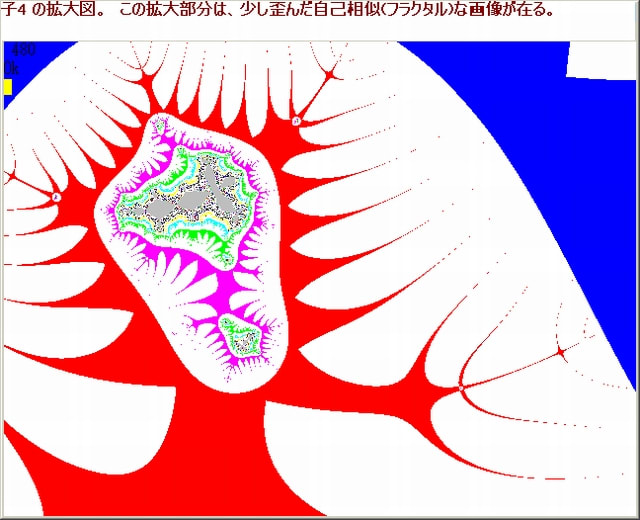
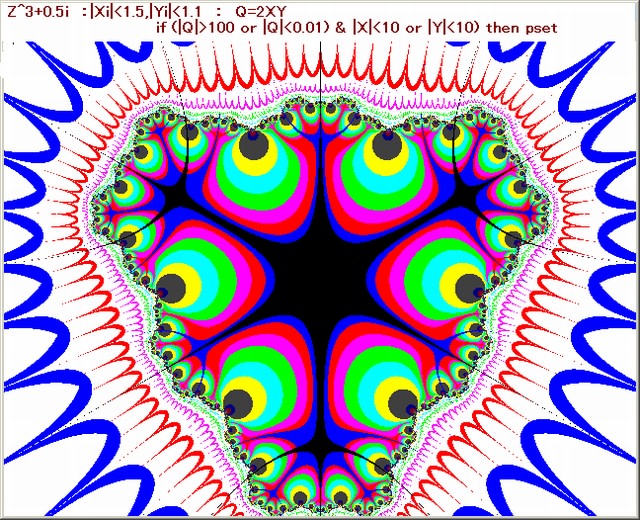
下図は、ひ孫1の画像である。この画像のモヤモヤとした黒い”噴煙”の中の一部を拡大する。

下図の中の 1 の枠部分を拡大する。( 2 の枠部分の拡大は実行していない。
その理由は、Nmax=500であるため実行時間が余りに膨大となるため実行を断念した。)
なお、拡大枠を明確にするため、ひ孫1画像の”噴煙”部分の色は黒→黄色に変更してある。


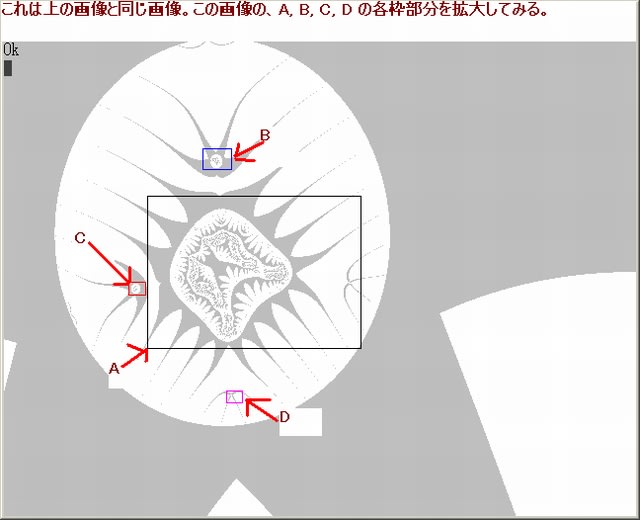
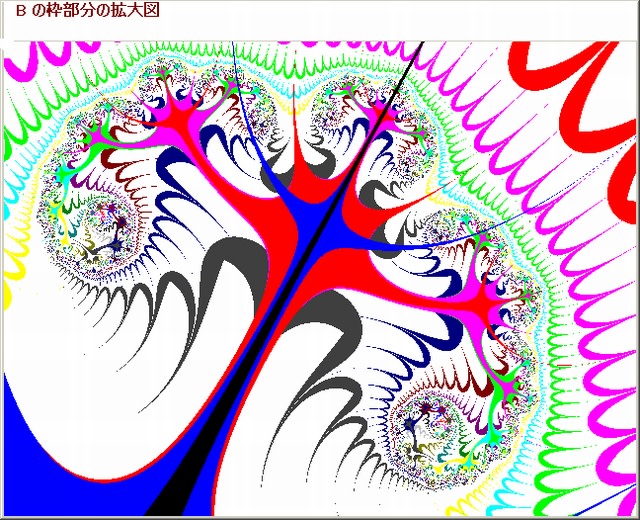
下図が 1 の枠部分の拡大図でである。ひ孫1画像の”噴煙”部分の中に見られる不規則に散在している点は、このように拡大してみても一塊りの大きさをもったモノとはなっていない。相変わらず不規則な点が散在している。

上図より分かることは『”噴煙”部分の中の不規則な点の散在』も自己相似(フラクタル)な画像となっていることだ。
しかも、弓状の線も存在している。この図の場合、この線の色は、暗い黄色のみである。
このことは此の弓状の線は14の整数倍(但し500以下)のN値で、N-loopを脱出していることを意味している。
また上図にランダムに散在する点は、よく見ると、白色が圧倒的に多い。
上図では其れは確認しずらいが、オリジナル画像で見ると其れが確認できる。
これらの点が白色だということは或るN値でN-loopを脱出しているが、しかし画像作成条件のpset条件を満足していない点であることを意味している。
***
ここで、少し整理すると以下のように言えると思われる。
1. (sinZ)^2 +0.5 画像の、黒いモヤモヤとした”噴煙”は、N-loopを脱出出来ず、N-loopを貫通してしまうような、N-loopの入力点(Xi,Yi)の集合である。
ここでNmax=500である。(前記事の最後で述べたように、これらは、ある意味で「発散しない」点の集合と言える。)
2. ”噴煙”の中に点在する白い点は、N-loopを或るN値(<=500)で脱出するが、pset条件を満足しない(即ち、N-loop脱出時のX,Yが『|X|<10 or |Y|<10』を満足しないような)、N-loopの入力点(Xi,Yi)の集合である。
3. ”噴煙”の中に点在する点で白色でない点は、その色に相当するN値でN-loopを脱出して、かつ、pset条件を満足するN-loopの入力点(Xi,Yi)の集合である。(ここで、色C=N MOD 16である。)
4. ”噴煙”の中に点在する点も自己相似(フラクタル)な画像となっている。
5. (sinZ)^2 +0.5 画像に弓状に走る線については其の性質は、よく分からないが、少なくとも”噴煙”部分を拡大しても存在している。
以上である。