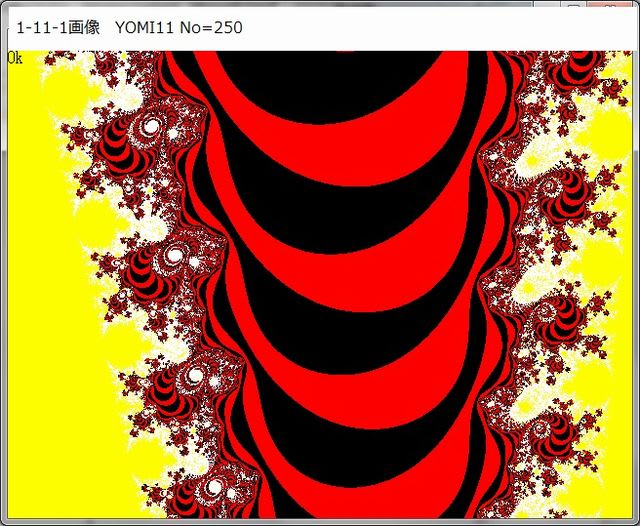
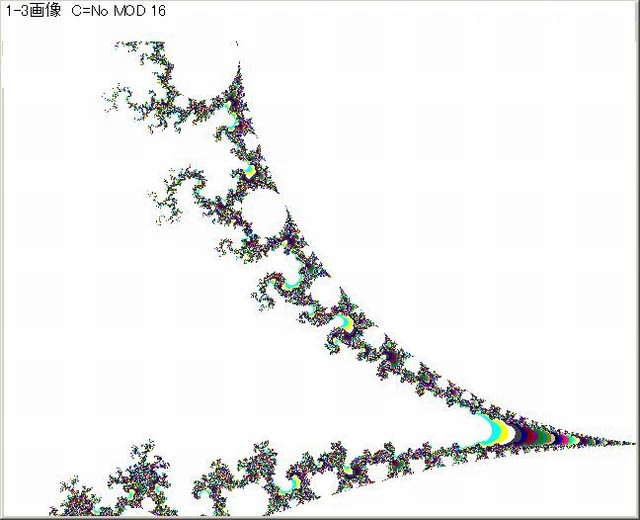
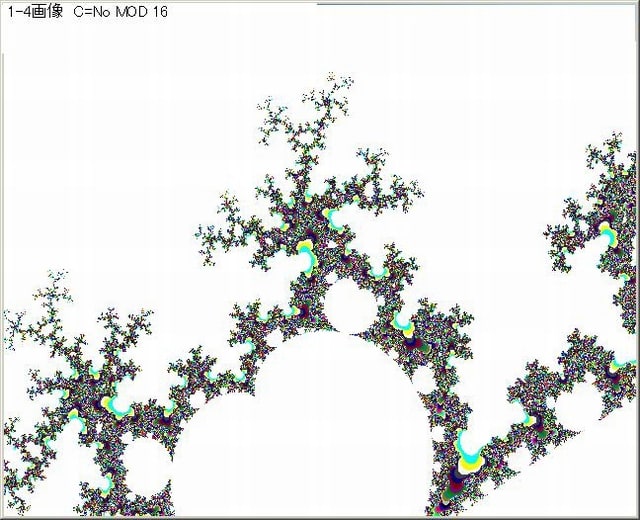
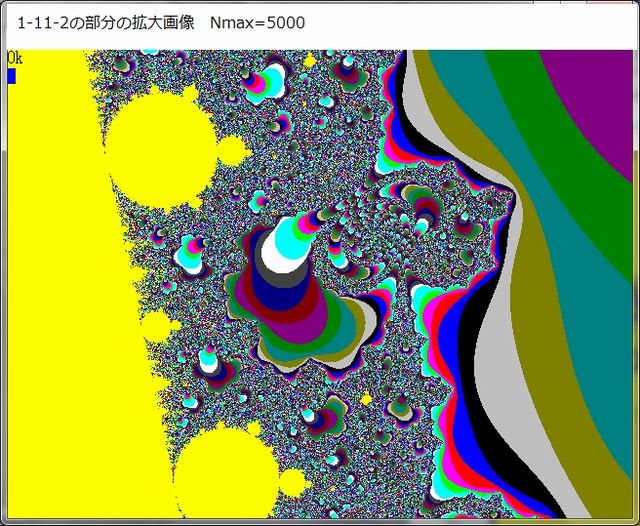
前記事262記載の1-11-2画像は特に面白い画像であった。
下図は、その画像である。


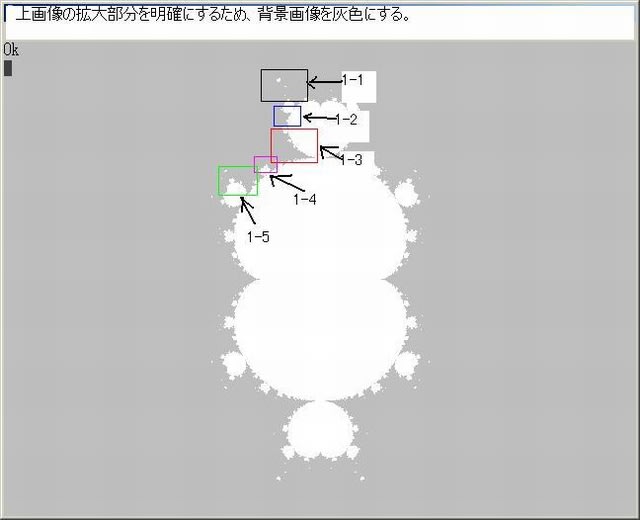
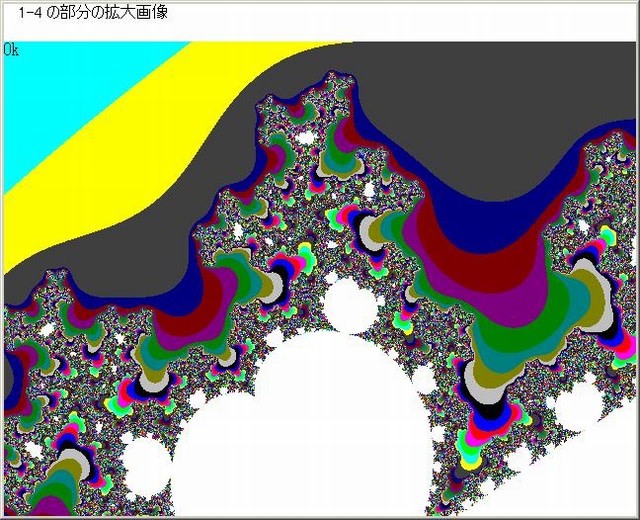
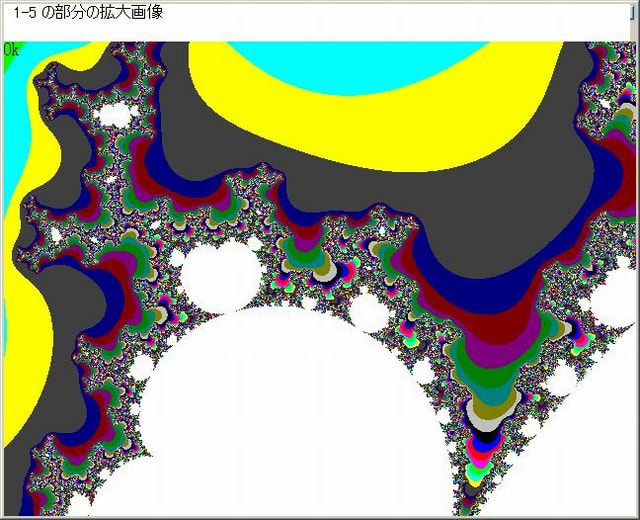
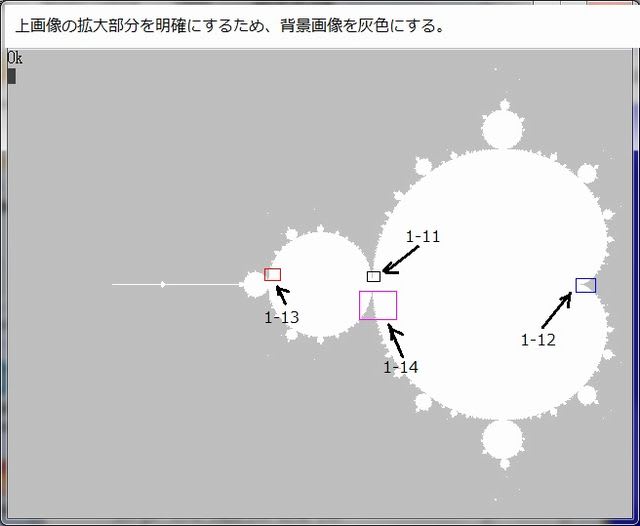
ここで、下図のように1-11-2画像の中の4個所の部分を選ぶ。


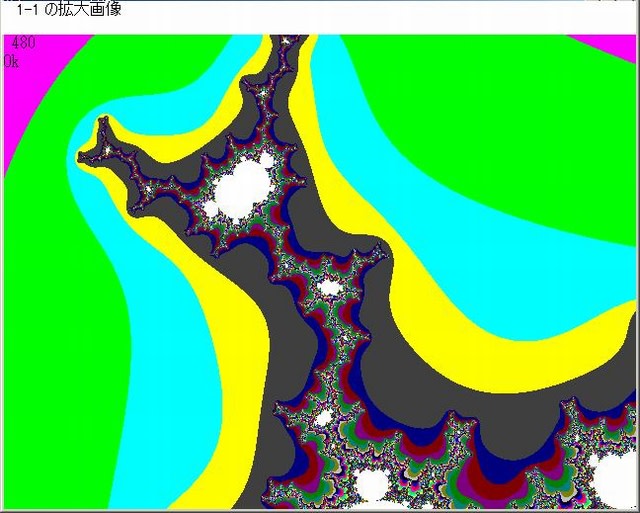
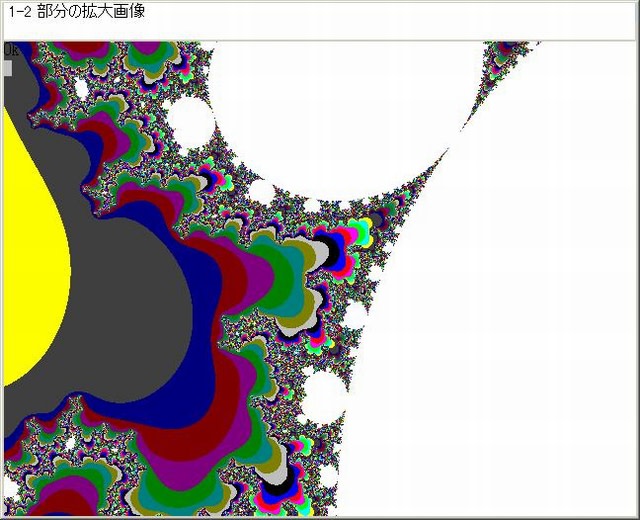
下図はそれらの各拡大画像である(1-11-2-1~1-11-2-4)。
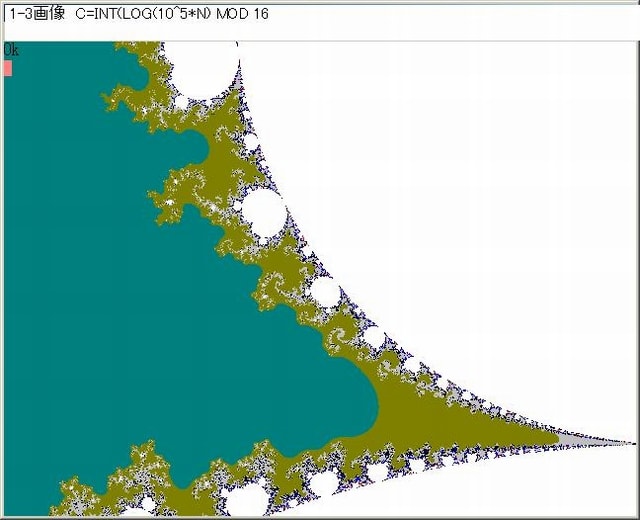
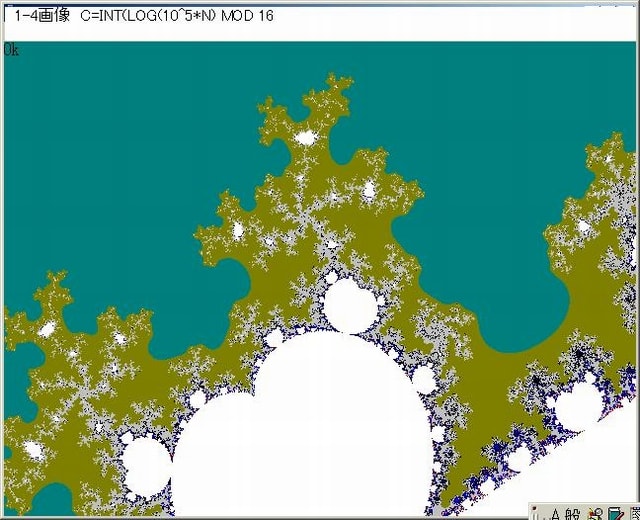
ここで、各画像において、オリジナル画像(C=No MOD 16)とLOG(No)画像と赤黒縞模様画像を並べて表示する。赤黒縞模様画像を以後便宜上『縞蛇画像』と名付ける。
縞蛇画像は、Noが偶数の時は赤、奇数の時は黒としている。また、NaをNmax以下のNoとして、NoがNa以上の場合は表示していない。そうすることによって、縞蛇の画像の構成が分かりやすくなる。
1-11-2-1 画像


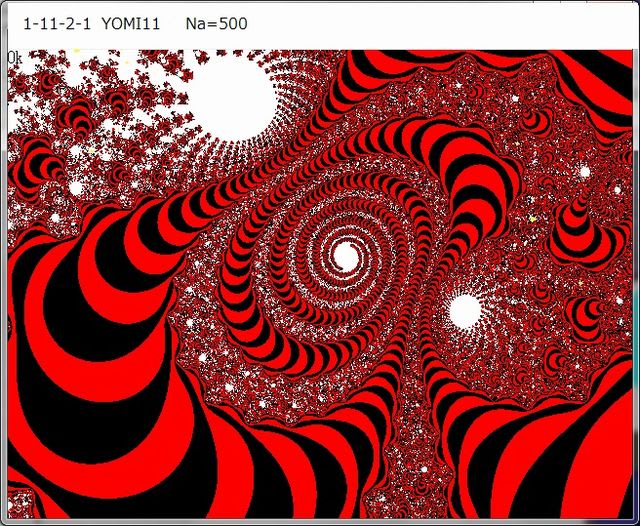
-----------------------------------------------------------
1-11-2-2 画像

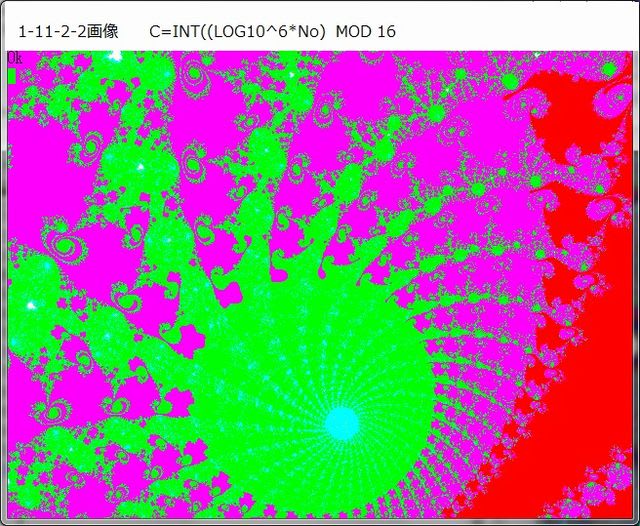
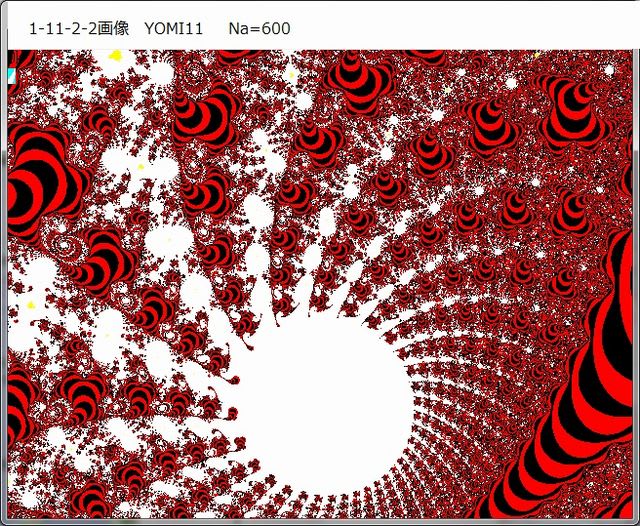
----------------------------------------------------------
1-11-2-3 画像



----------------------------------------------------------
1-11-2-4 画像

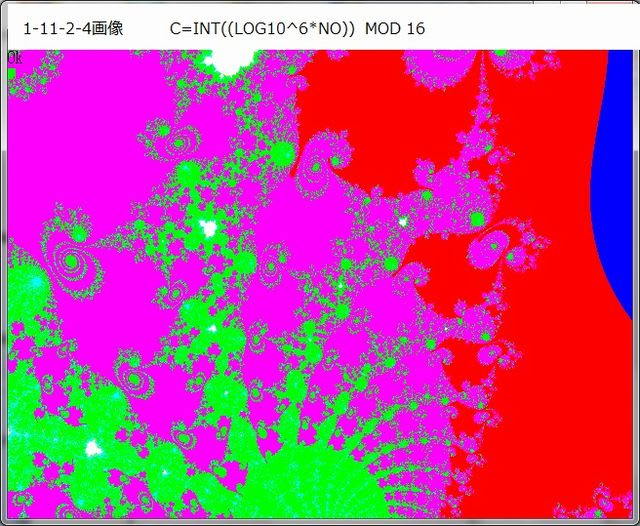

-----------------------------------------------------------
以上の画像から分かることは、これらの画像には特異点らしきものが存在するということ。その特異点とは、特に縞蛇画像で見られるように、縞蛇が画像のある一点へと収束していて、その収束の仕方は少なくとも2種類存在する。
その一つは一匹の縞蛇の『尾』が『ら線』状に、ある一点へと巻き付いて接近していく、ということ。
もう一つの収束の仕方は複数の縞蛇の各々『尾』が『環』状になって、ある一点へと接近していくということ(画像から見るとアメーバー状に見え、それらが縮んでいくように見える(特にLOG(No)画像において)。
渦巻状とアメーバー状の画像は、画像の随所に見られる。
またLOG(No)画像のアメーバー状模様は、あたかも水滴が落下して散乱した模様にも似ている。あるいは、窓硝子へ当たった雨水の滴(しずく)にも似ている。
これらの画像をザックリと見ると、細かい構造は違うが共通した画像構造が存在するように見えて面白い。
この構造は画像の大きさには関係ないらしい。
下図は、その画像である。



ここで、下図のように1-11-2画像の中の4個所の部分を選ぶ。


下図はそれらの各拡大画像である(1-11-2-1~1-11-2-4)。
ここで、各画像において、オリジナル画像(C=No MOD 16)とLOG(No)画像と赤黒縞模様画像を並べて表示する。赤黒縞模様画像を以後便宜上『縞蛇画像』と名付ける。
縞蛇画像は、Noが偶数の時は赤、奇数の時は黒としている。また、NaをNmax以下のNoとして、NoがNa以上の場合は表示していない。そうすることによって、縞蛇の画像の構成が分かりやすくなる。
1-11-2-1 画像



-----------------------------------------------------------
1-11-2-2 画像



----------------------------------------------------------
1-11-2-3 画像



----------------------------------------------------------
1-11-2-4 画像



-----------------------------------------------------------
以上の画像から分かることは、これらの画像には特異点らしきものが存在するということ。その特異点とは、特に縞蛇画像で見られるように、縞蛇が画像のある一点へと収束していて、その収束の仕方は少なくとも2種類存在する。
その一つは一匹の縞蛇の『尾』が『ら線』状に、ある一点へと巻き付いて接近していく、ということ。
もう一つの収束の仕方は複数の縞蛇の各々『尾』が『環』状になって、ある一点へと接近していくということ(画像から見るとアメーバー状に見え、それらが縮んでいくように見える(特にLOG(No)画像において)。
渦巻状とアメーバー状の画像は、画像の随所に見られる。
またLOG(No)画像のアメーバー状模様は、あたかも水滴が落下して散乱した模様にも似ている。あるいは、窓硝子へ当たった雨水の滴(しずく)にも似ている。
これらの画像をザックリと見ると、細かい構造は違うが共通した画像構造が存在するように見えて面白い。
この構造は画像の大きさには関係ないらしい。