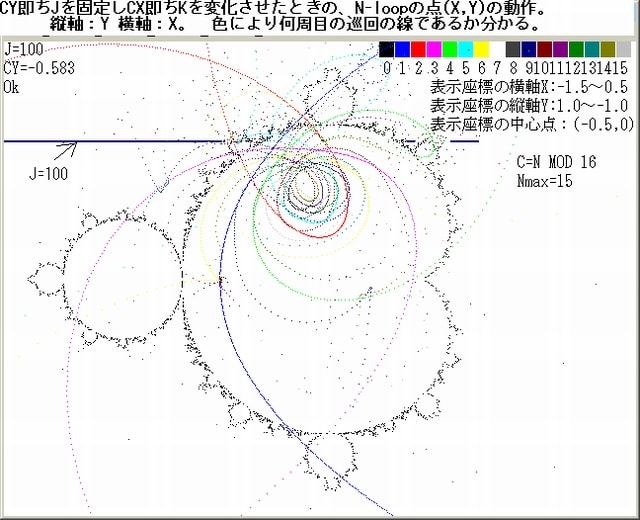
前記事の画像で、J=100以下では、ある種の規則性が見られたが、J=120では一変して画像が無秩序になっている。今回は、この変化の様子をみてみよう。
***
先ず、今までの画像について復習しよう。
***
1.画像表示の領域:Dの一点Z0を考える。
***
2.この点Z0の座標を極座標で表し、Z0(R,θ)とする。
***
3.ここでRはDの中心(-1.4,0)・・・これはマンデルブロ集合の重心でもある・・・からの距離とし、θは原点からの角度とする。
***
4.ここで、先ずRを固定して、θ=0度の点Z0を始点としてN-loopでの点列:Z0,Z1,Z2,・・・Zn,・・・,Zmaxを計算し表示していく。
ここで計算が終了したら、次の始点Z0(R,θ+dθ)に移り、再度、点列:Z0,Z1,Z2,・・・Zn,・・・,Zmaxを計算し表示していく。
( ここで点列計算での初期値:X,Yは0に戻しておく )
***
5.上記計算の場合、N-loopの巡回回数を0~15としておく。即ち、点列は
Z0,Z1,Z2,・・・Zn,・・・,Z15 ・・・・・・・・・・・・・・・(1)
となる。ここで各点列に色:Cをつける。C=Nとする。(下記の注を参照)
6.上記4項を、θ→360度になるまで繰り返す。
--------------------------------------------------------
ここまでの画像は以下を表している。
即ち『Rが一定で、θ=0度→360度にしていったときの各θの点列(1)が重なった画像である。』
***
そして、『同じ色の点は、各点列において同じn番目のZnであることを表している。
同じ色の点が連続した軌跡となっているのは、各θ値でのZnが連続していることを意味している。』
***
Rが小さい場合は( 例えば、J=40(R=0.22) )、この色の配置はある規則性をもっている。
( 色を見れば、各θでのZnの動作(振動して小さくなっていく等の)が分かる。)
***
以下の画像は、J=100(R=0.57)~J=120(R=0.68)の画像である。J→大程画像が『無秩序』になっていくが、その『無秩序』の一つの内容は、『各θでのZnに相互関連性がなくなっていく』ということであり、それが軌跡の色の混乱(無秩序)として表れている、とも言えそうだ。
***
この無秩序性はRに依存しているから、Rをパラメータとして、この『無秩序性』の別の表現はあるだろうか?
(注:下図において、Nmax=16としているが、N-loopは、N=0から始めているのでNmax=15とすべきであったが、画像そのものには、本質的にはあまり影響はないと思う。)
-----------------------------------------------------------------









***
先ず、今までの画像について復習しよう。
***
1.画像表示の領域:Dの一点Z0を考える。
***
2.この点Z0の座標を極座標で表し、Z0(R,θ)とする。
***
3.ここでRはDの中心(-1.4,0)・・・これはマンデルブロ集合の重心でもある・・・からの距離とし、θは原点からの角度とする。
***
4.ここで、先ずRを固定して、θ=0度の点Z0を始点としてN-loopでの点列:Z0,Z1,Z2,・・・Zn,・・・,Zmaxを計算し表示していく。
ここで計算が終了したら、次の始点Z0(R,θ+dθ)に移り、再度、点列:Z0,Z1,Z2,・・・Zn,・・・,Zmaxを計算し表示していく。
( ここで点列計算での初期値:X,Yは0に戻しておく )
***
5.上記計算の場合、N-loopの巡回回数を0~15としておく。即ち、点列は
Z0,Z1,Z2,・・・Zn,・・・,Z15 ・・・・・・・・・・・・・・・(1)
となる。ここで各点列に色:Cをつける。C=Nとする。(下記の注を参照)
6.上記4項を、θ→360度になるまで繰り返す。
--------------------------------------------------------
ここまでの画像は以下を表している。
即ち『Rが一定で、θ=0度→360度にしていったときの各θの点列(1)が重なった画像である。』
***
そして、『同じ色の点は、各点列において同じn番目のZnであることを表している。
同じ色の点が連続した軌跡となっているのは、各θ値でのZnが連続していることを意味している。』
***
Rが小さい場合は( 例えば、J=40(R=0.22) )、この色の配置はある規則性をもっている。
( 色を見れば、各θでのZnの動作(振動して小さくなっていく等の)が分かる。)
***
以下の画像は、J=100(R=0.57)~J=120(R=0.68)の画像である。J→大程画像が『無秩序』になっていくが、その『無秩序』の一つの内容は、『各θでのZnに相互関連性がなくなっていく』ということであり、それが軌跡の色の混乱(無秩序)として表れている、とも言えそうだ。
***
この無秩序性はRに依存しているから、Rをパラメータとして、この『無秩序性』の別の表現はあるだろうか?
(注:下図において、Nmax=16としているが、N-loopは、N=0から始めているのでNmax=15とすべきであったが、画像そのものには、本質的にはあまり影響はないと思う。)
-----------------------------------------------------------------