300 Z^2マンデルブロ集合画像とブッダブロ集合画像を重ねた画像

下図はZ^2マンデルブロ集合画像の近似境界(赤線)と、記事294の最後のブッダブロ集合画像を重ね合わせた画像である。それらの画像の位置関係が分かる。

(注：『記事294の最後のブッダブロ集合画像』は、Z^2マンデルブロ集合内の全ての点を始点とした場合のlog画像である。詳細は記事294を参照。)

299 Z^2マンデルブロ集合におけるブッダア゛ロ点列について(その4)

前記事において、問題は両プログラムにおける次のコマンドにあるのではないかと書いた。
即ち、　Q=X^2+Y^2:IF Q>4 THEN ***
巡回ループ脱出条件である。両プログラムにおいて、X,Yの僅かな差が巡回ループを巡回するとき増幅されて、上の脱出条件に差が出ることは考えられることである。
***
次のプログラムを作って、それを確認してみた。
***
10 REM マンデルブロ集合画像作成プログラムと点列表示プログラムのQの差
20 REM DATA3Zはンデルブロ集合の尻の座標データ
190 CONSOLE ,,0,1
210 COLOR 0,7,,,2
230 CLS 3
240 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",242,ALL
242 ON ERROR GOTO 50000
248 REM マンデルブロ集合画像作成プログラム
250 CXS=-1.5:CXE=0.5:DX=(CXE-CXS)/480:M=0:V=0
270 CYS=-1:CYE=1:DY=(CYE-CYS)/480
390 OPEN "C:\BASIC1\TEST\DATA3Z.DAT" FOR INPUT AS #1
400 OPEN "C:\BASIC1\TEST\Q1.DAT" FOR OUTPUT AS #4
410 INPUT #1,X,Y,K,J,N
430 IF EOF(1) THEN 2030
450 PSET (K,J),0
570 CX=CXS+DX*K
580 CY=CYS+DY*J
1430 X=0:Y=0
1450 FOR N=0 TO 500
1470 XX=X^2-Y^2+CX
1490 Y=2*X*Y+CY
1510 X=XX
1530 Q1=X^2+Y^2
1531 V=V+1:LOCATE 0,0:PRINT V
1540 WRITE #4,Q1
1550 NEXT N
1858 GOTO 410
2030 CLOSE
2040 '
3000 REM 点列の表示プログラム
3010 CXS=-1.5:CXE=0.5:DX=(CXE-CXS)/480
3012 CYS=-1:CYE=1:DY=(CYE-CYS)/480
3130 OPEN "C:\BASIC1\TEST\DATA3Z.DAT" FOR INPUT AS #1
3140 OPEN "C:\BASIC1\TEST\Q2.DAT" FOR OUTPUT AS #4
3160 INPUT #1,X,Y,K,J,N
3170 IF EOF(1) THEN 3620
3200 PSET (K-50,J),0
3210 CX=CXS+DX*K
3220 CY=CYS+DY*J
3270 X=0:Y=0
3280 FOR N=0 TO 500
3290 XX=X^2-Y^2+CX
3300 Y=2*X*Y+CY
3310 X=XX
3320 Q2=X^2+Y^2
3321 M=M+1
3322 LOCATE 0,1:PRINT M
3330 WRITE #4,Q2
3360 NEXT N
3470 GOTO 3160
3620 CLOSE
3640 END
***
1530行のQと3320行のQとの差の最大値を以下のプログラムで求めてみた。
***
10 REM マンデルブロ集合画像作成プログラムと点列表示プログラムのQの差
20 REM DATA3Zはンデルブロ集合の尻の座標データ
190 CONSOLE ,,0,1
210 COLOR 0,7,,,2
230 CLS 3
240 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",242,ALL
242 ON ERROR GOTO 50000
400 OPEN "C:\BASIC1\TEST\Q1.DAT" FOR INPUT AS #1
404 OPEN "C:\BASIC1\TEST\Q2.DAT" FOR INPUT AS #2
406 QMAX=0
440 INPUT #1,Q1
444 IF EOF(1) THEN 530
450 INPUT #2,Q2
452 LOCATE 0,0:PRINT Q1
454 LOCATE 0,1:PRINT Q2
500 Q=ABS(Q1-Q2)
510 IF Q>QMAX THEN QMAX=Q
520 GOTO 440
530 LOCATE 0,10
540 PRINT "Qmax=";QMAX
550 CLOSE
600 END
***
上のプログラムの実行結果は、Mmax=0
であった。両プログラムにおいて、『Q=X^2+Y^2:IF Q>4 THEN ***』は全く問題ないという結果になった。

さてさて、ますます問題は混迷してきた・・・

(本件の問題は今回で中止することにする。)

298 Z^2マンデルブロ集合におけるブッダブロ点列について(その3)

Z^2マンデルブロ集合の『尻』部分の画像と、その画像作成プログラムを下に再掲する。





問題は、上のプログラムの始点入力の与え方が、点列集合画像の始点入力の与え方との若干の差にありそうだ、と先に記事に書いた。そこで、始点の与え方を両プログラムで全く同一にした。
下図が点列表示プログラムである。



上のプログラム結果は下図であるが、始点入力の与え方を変えないときの画像と全く同じ結果となった。『マンデルブロ画像の始点にブッダブロ点列の始点がある』という問題の理由は始点の与え方ではなかった。





そもそも問題は、『この記事の一番上のマンデルプロ画像の座標点が、『尻』画像プログラムの巡回ループ貫通するのに、その同一座標の点が、『点列表示』プログラムの巡回ループを脱出する』ということであった。

さて、次に問題となってくるのは脱出条件、
『Q=X^2+Y^2
IF Q＞2 THEN ***』
である。BASIC/98では、特に指定しない変数は倍精度実数型で処理する仕様になっている。

ここらあたりが、両プログラムで、異なって結果を生じさせている・・・ということも考えられる。果たしてそうだろうか?

果たして問題はそこまで発展するのだろうか。混迷は深み始めた。

297 Z^2マンデルブロ集合におけるブッダブロ点列について(その2)

もう一度画像を描いて再確認してみた。

Z^2マンデルブロ集合全体の点について再確認にするのは時間がかかるから、ブッダブロ点列が存在するZ^2マンデロブロ集合の『尻』部分のみ再確認することにした。

下図はその再確認の部分である。座標はパラメータ:K,Jで表現して、点(416,115)と点(416,367)を結ぶ線の右側のみとする。
(注:下図のX,YはそれぞれK,Jの記載ミスである。)





---------------------------------
下図が上図の『尻』画像の座標を始点とした点列集合画像である。
やはりブッダブロ点列集合が現れている。



-----------------------------------------
下図は、『尻』部分の画像及び、その座標(K,J)の始点データのファイル保存プログラムである。

(注:下図のプログラムにおいて、#1のOPENコマンドは書き忘れの記載ミスである。実際に実行したプログラムには記載している。)



----------------------------------------
下図は上図のプログラムで保存された座標データを読み込み、点列表示するプログラムである。




これらのプログラムから『同一な』座標が、『尻』表示プログラムでは巡回ループを貫通しているのに、点列表示プログラムでは巡回ループを脱出しているのである。これは矛盾である。

ここらから問題の原因が見えてきた、『同一な』座標は実は同一ではないのである。
即ち同一な点(K,J)でも、それが点(X,Y)に変換されるとき同一ではなくなっているのであろう。

つまり、二つのプログラムにおいてDXとDYが厳密には異なっている。
その微妙な違いが画像の差になっていると思われる(未確認だが)。

つまり、それほど、『尻』部分の座標の差は微妙で、それが巡回ループを脱出させたり貫通ざたりしていると思われる。

296 Z^2マンデルブロ集合におけるブッダブロ点列について。

Z^2マンデルブロ集合の点座標を始点とした点列に、ブッダブロ点列が現れるか否か、再度、マウス・クリックで再確認した。始点をマウスでクリックして与える方法である。点列が青色になればブッダブロ点列である。赤色になれば貫通点列である。マンデルブロ集合の『尻』部分にブッダブロ点列が現れることは前より分かっていた。そこで、その確認もした。以下の結果の画像である。









---------------------------------------------------
記事264の結果(マンデルブロ集合の点を始点とする点列にブッダブロ点列が存在すること)と上図の一番上の図とは矛盾はしていない。マンデルブロ集合座標の『尻』部分の座標値を始点とする点列は確かにブッダブロ点列となっている。しかし、これはどうも納得できない。
そこで初めに戻って少し整理てみよう。私は何か勘違いていないか。

***

いま、複素平面において画像を表示したい複素座標をD(X,Y)とする。Xは実軸上の値、Yは虚軸上の値とする。ここで、Dの中の点Z(X,Y)とし、次の巡回式を考える。
巡回式: Z(X,Y)←Z(X,Y)^2+Z0(X0,Y0)・・・・・・・・・・・・・・(1)
ここでZ0(X0,Y0)はD内の固定値(定数)とする。
また変数:X,Yの初期値は共に0とする。
また巡回式の最大巡回回数も決めておき、それをNmaxとする。

***

X,Yの初期値は共に0だから、Z(X,Y)^2=0 故、(1)より複素平面上に以下の点列が得られる。
Z0,Z1,Z2,・・・・,ZNmax・・・・・・・・・・・・・・・・・・・・・・・・・・・・(2)

***
マンデルブロ集合とは、Nmax→∞の場合でも『発散しない』ような点Z0の集合である。

***
ここで、(2)の点列で、|Zn|=(X^2+Y^2)^0.5＞2 ・・・・・・(3)
となったとしよう。その場合は『発散した』とする。

***
そこでマンデルブロ集合とは、(3)を満足しないD内の点Z0の集合とする。
( ここで、(2)の点列を新たに求めるときは、即ち、Z0を変える場合は、
変数:X,Yの初期値は0にする。)

***
次に、ブッダブロ点列とは、以下のように定義する。

点列(2)が、Znで(3)を満足したとき、以下の点列をブッダブロ点列とする。
Z0,Z1,Z2.・・・,Zn・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・(4)
***
ブッダブロ集合とは、(4)となるD内の全ての点Z0の集合:Aとする。
ブッダブロ画像とは、Aの全ての点列(4)の集合画像を言うものとする。

***
貫通点列とは、以下のように定義する。
点列(2)において、(3)を満足しないとき、(2)の点列を貫通点列と定義する。
貫通集合とは、(2)となるD内の全ての点Z0の集合:Bとする。
貫通画像とは、Bの全ての点列(2)の集合画像とする。

-----------------------------------------------------------------------

上の定義からすれば、マンデルブロ集合を始点とする点列は貫通点列しか存在しえない。
しかし画像結果は『マンデルブロ集合を始点とする点列にブッダブロ点列が存在していた。
のみならず、その点列集合は明らかにブッダブロ画像となっていた→記事295の結果。
ということは、結局、私の画像作成プログラムにバグというよりプロミングミスがあることしか考えられない。

****

記事292,293の『マンデルブロ集合の縁(ふち)の画像』結果については上記した点列定義と矛盾していない。

問題があるとしたら、記事295の、マンデルブロ集合との与え方と、それによる点列画像プログラムに不具合があることしか考えられない。

295 Z^2マンデルブロ集合の全ての点(K,J)を始点とする点列の集合(その2)

前回の記事では、マンデルブロ集合の全ての点(K,J)を始点とする点列の集合には、ブッダブロ点列の集合も含まれていることを書いた。そして、その集合を画像化してみると、ブッダブロー画像になることも確認した。

***
以下にマンデルブロ集合画像と、その画像の全てを始点とする点列を求めるプログラムを再掲しておく。




---------------------------
上記プログラムのN-loopの後の貫通点列をデータ・フアイルに書き込み、そのデータを読み出して、LOG(m)化表示したのが下図である(上記プログラムの生データは紛失してしまった)。

下図が、貫通点列のLOG(m)の集合画像であるが、ここで m は貫通点列が同一座標になる回数(濃度)で、色:C=LOG(m)で表している。この図で分かるように画像の中央部近辺が m が大きいことが分かる。色から判断して、C=7.5～8.5 即ち、m=e^7.5 ～e^8.5=1800～4900程度だと分かる。



----------------------------
以前の記事286で『ループ内画像』を紹介した。この画像の詳細は、記事286をみていただくとして、この画像を下に再掲しておく。



-----------------------------
この『ループ内画像』と『貫通点列』画像は酷似している。画像の中央部あたりが若干違う程度である。これらの画像の定義からして酷似するのは当然であるが、それよりも私が疑問に思っているのは、前回の記事264で書いたこと、即ち、『マンデルブロ集合の全ての点(K,J)を始点とする点列の集合』に、なぜ、ブッダブロ点列があるか?　という疑問である。果たして、これは事実なんだろうか?

294 Z^2マンデルブロ集合の全ての点を始点とする点列の集合画像(その1)

前記事ではマンデルブロ集合の縁(ふち)の画像の全ての点(K,J)を始点とする点列の集合画像を求めた。この縁は厳密には真の縁ではなく、真の縁の外側の画像であるため、得られた画像はブッダブロ点列のみの集合画像であることも確認した。

***
では、マンデルブロ集合の全ての点(K.J)を始点とする点列の画像は、どのような画像になるのだろうか。今回はそれを調べる。

***
そもそもマンデルブロ集合とは巡回ループを脱出しない点の集合である。従って、マンデルブロ集合の全ての点(K.J)を始点とする点列は、上の定義上、ブッダブロ点列は存在しないはずである。存在するのは貫通点列の集合画像となるはずである。

***
下図はマンデルブロ集合画像(緑色)と、その画像作成プログムである。





---------------------------------------------------

下図はマンデルブロ集合の全ての点を始点とする点列の集合画像を求めるプログラムと、その実行結果である。『貫通点列』は赤色、『ブッダブロ点列』は青色で描くようにしている。また各点列は、それぞれ別のデータファイルに保存するようにしてある。





---------------------------------------------------
上図から分かるように、予想の反して、ブッダブロ点列(青色)も存在している!!??
赤色、即ち貫通点列が圧倒的に多いのは当然だとしても、青色、即ちブッダブロ点列が存在するのは意外であった。(参照としてマンデルブロ集合の縁を赤線で示してある。)
各点列のデータ容量は、貫通点列(赤色)は、546,585KB。ブッダブロ点列(青色)は、3,879KB
であった。

***
上図においては、赤色(貫通点列集合)が青色(ブッダブロ点列集合)をマスクしている可能性がある。そこで、ブッダブロ点列集合(青色)のみを表示させてみた。その結果が下図である。





-------------------------------------------------------------
上図に示すように、なんと驚くべき画像が現れた。これはブッダブロ画像ではないか!!!

ブッダブロ点列の集合だからブッダブロ画像となる、と言えばそれのでだが、しかし、この点列の始点はマンデルブロ集合そのものなのである。マンデルブロ集合の内部(と断言するのは危険だが)に実はブッダブロ点列が内在しているのだ!!!

***
そう言えば、マンデルブロ集合の縁画像をクリックして調べているとき、マンデルブロ集合の『尻』
近辺にブッダブロ点列が多く見られた。(記事259の最後の図を参照)

上図においても、その現象が見られる(LOG(m)画像参照)。
また、始点とは全く異なる座標が点列が同時発生する現象も見てきた。
これらの点も『マンデルブロ集合を始点とする点列にブッダブロ点列がある』ということの一理由かもしれない。

***
『マンデルブロ集合を始点とする点列にブッダブロ点列がある』ということは、知る人は知っているあたりまえのことかも知れないが、私は驚いた。と同時に、マンデルブロ画像の奥行の深さを
思い知らされた。
***
では、貫通点列の画像はどうなるだろうか？

貫通点列(赤色)は、546,585KB　もある。このデータを読み出すのも一苦労である。このデータ結果をみて、『マンデルブロ集合を始点とする点列にブッダブロ点列がある』ということを調べてみよう。

293 Z^2マンデルブロ集合の縁の座標dataの読み出しによる点列画像

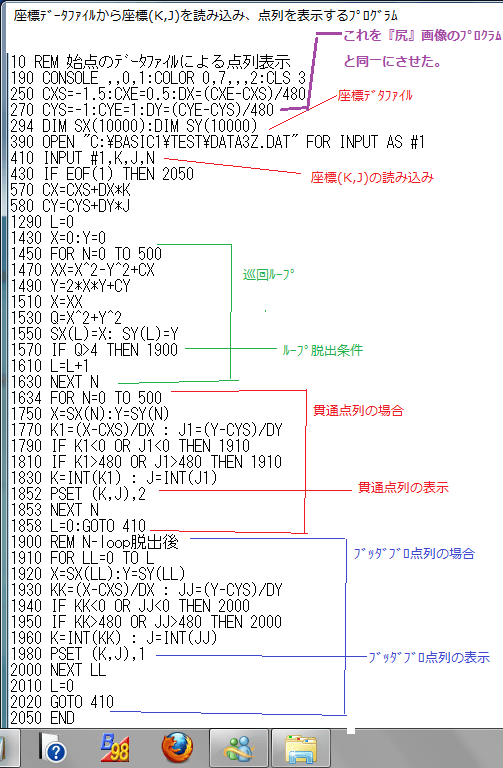
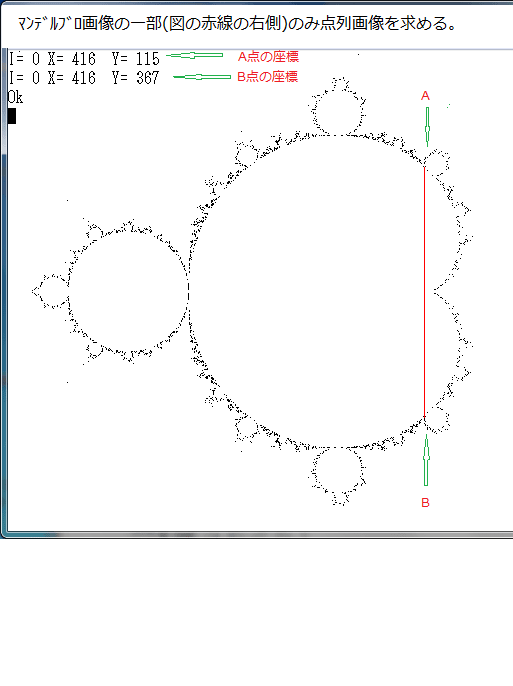
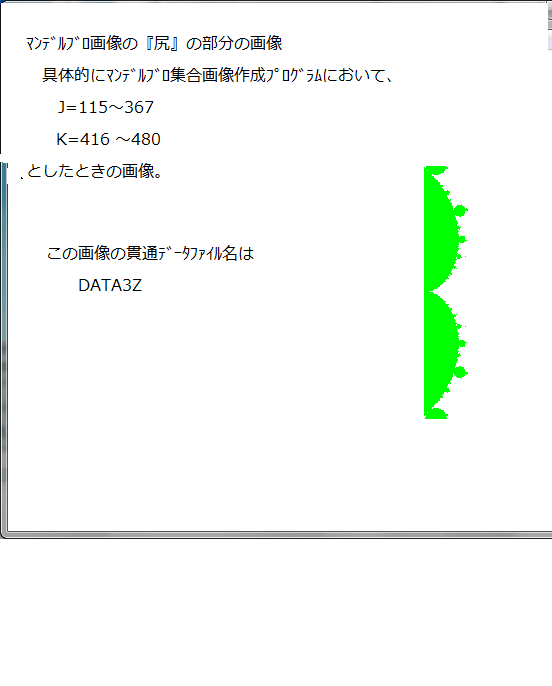
前記事262で、マンデルブロ集合の縁の画像を求める一例を説明した。
この方法での縁の座標データをdata file化しておき、それを順次読みだして点列画像を求めるプログラムを作り、画像を求めた。

***
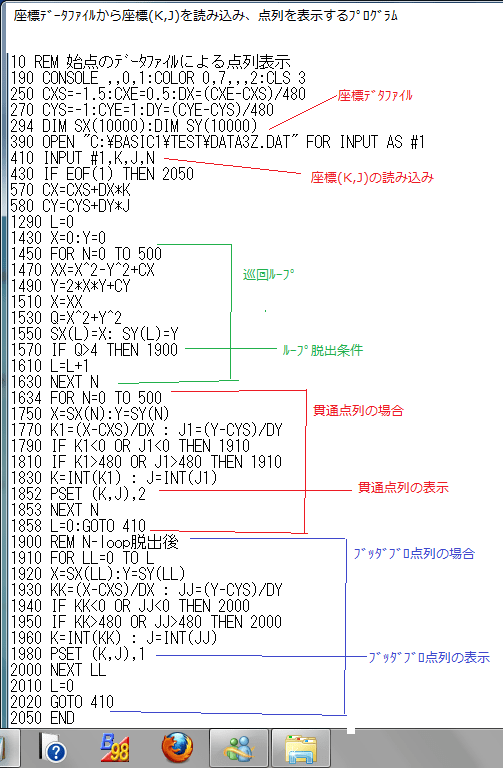
このプログラムは最後に参考として書いておくが、要点だけ先に説明しておく。

要するに、巡回ループを貫通してしまう場合は、その時点の過去の点列は赤く表示する(『貫通点列』)。また、巡回ループを脱出する場合は、その時点の過去の点列を青く表示する(『ブッダブロ点列』。



***

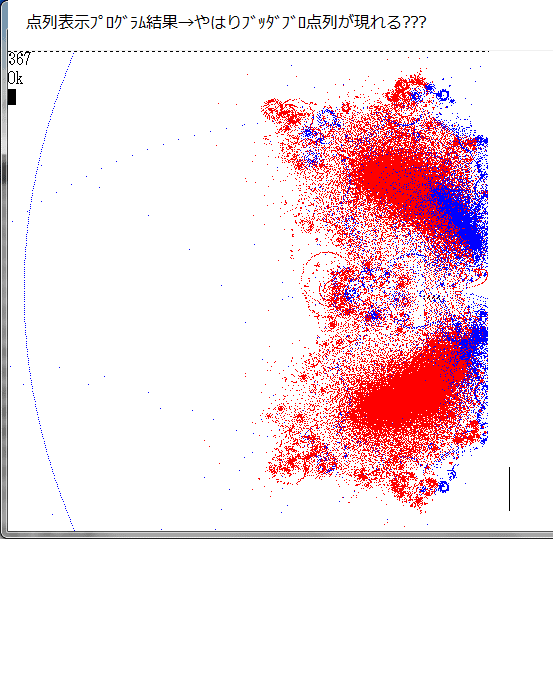
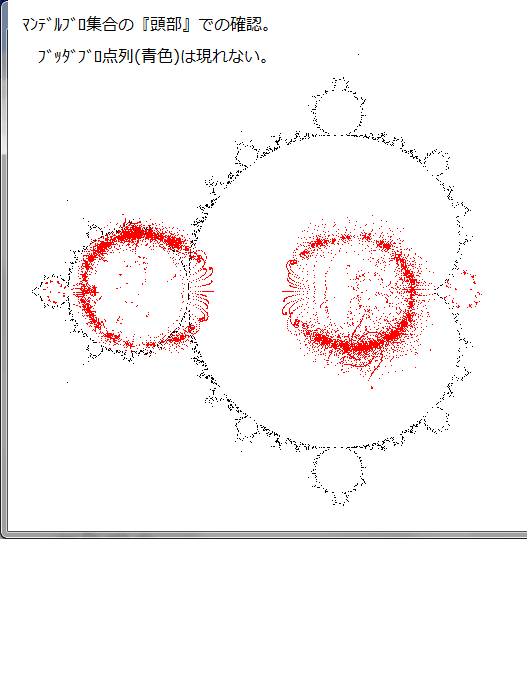
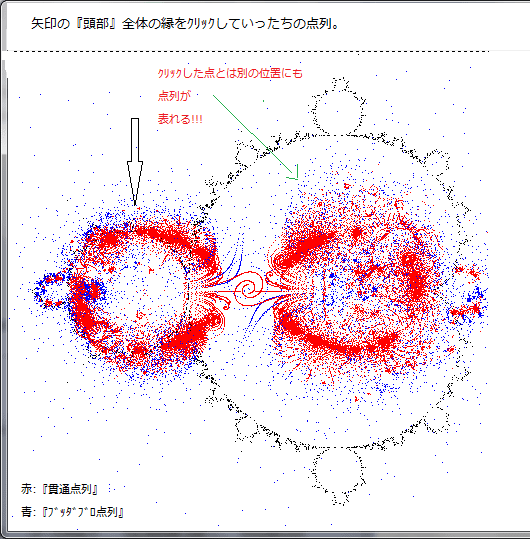
下図が、このプログラムの実行結果である。





------------------------
上図から分かるように、表示されたのは青い『ブッダブロ点列』のみである。
赤い『貫通点列』は一つも見いだせない。

***
前記事にも書いたように、この画像で使用したマンデルブロ集合の縁画像は真のマンデルブロ集合の縁の外側にある。

***
マンデルブロ集合の真の縁とは数学的には巡回ループを脱出するには無限回の巡回を必要とする点(K,J)の集合だろう。

そのような真の縁を具体的に実現するのは不可能だが、可能だとして、その理想化された点(K,J)では点列は、やはり『ブッダブロ点列』を示すと思われるが、もし、その理想化された点(K,J)に対して点(K-ε,J-ε)では『貫通点列』となるのだろうか?
(ここで、εは任意の小さな数である)

***
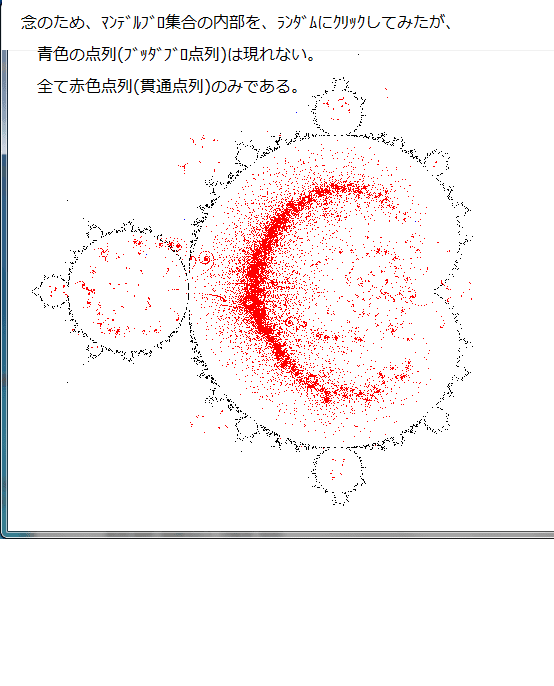
実はマデルブロ集合内部でも、『ブッダブロ点列』自体は存在する。
そもそも『ブッダブロ画像』とは、その典型である。
下図はその一例である。始点は乱数で与えている。そもそもブッダブロ画像はマンデルブロ集合内部の点列の画像でもあるのだから。



***

問題は、『ブッダブロ点列』を生成する始点がマンデルブロ集合内(縁も含めて)に存在するのか、ということである。

定義からして、『ブッダブロ点列』とは巡回ループを脱出した始点での過去の点列であり、マンデルブロ集合とは巡回ループを脱出しない始点の集合であるから、存在しないように思える。あたりまえのことか!?

***
以下は参考のために、ここで使用したBASIC/98のプログラムを下記しておく。
***
10 REM マンデルブロ集合の縁(ふち)data file:DATAマンデルAを順次読みだして
12 REM 点列を求める。重ね描きする。
14 RRM 『貫通点列』→赤、『ブッダブロ点列』→青　とする。
190 CONSOLE ,,0,1
210 COLOR 0,7,,,2
230 CLS 3
250 CXS=-1.5:CXE=0.5:DX=(CXE-CXS)/480
270 CYS=-1:CYE=1:DY=(CYE-CYS)/480
290 I=0:II=0:N1=0:NN=0
294 DIM SX(10000):DIM SY(10000):DIM Z1(480,480):DIM Z2(480,480)
330 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",350,ALL
350 ON ERROR GOTO 50000
370 REM マンデルブロ集合の縁(ふち)の表示
390 OPEN "C:\BASIC1\TEST\DATA3B.DAT" FOR INPUT AS #1
392 OPEN "C:\BASIC1\TEST\DATAK.DAT" FOR OUTPUT AS #2
394 OPEN "C:\BASIC1\TEST\DATAD.DAT" FOR OUTPUT AS #3
410 INPUT #1,KK,JJ,K,J
430 IF EOF(1) THEN 2030
440 LOCATE 0,0:PRINT USING "###";K
441 LOCATE 0,1:PRINT USING "###";J
450 PSET (K,J),15
570 CX=CXS+DX*K
580 CY=CYS+DY*J
610 '
1270 REM 画像の作成
1290 L=0
1410 REM N-loopの計算
1430 X=0:Y=0
1450 FOR N=0 TO 500
1470 XX=X^2-Y^2+CX
1490 Y=2*X*Y+CY
1510 X=XX
1530 Q=X^2+Y^2
1550 SX(L)=X: SY(L)=Y
1570 IF Q>4 THEN 1900
1610 L=L+1
1630 NEXT N
1634 FOR N=0 TO 500
1750 X=SX(N):Y=SY(N)
1770 K1=(X-CXS)/DX : J1=(Y-CYS)/DY
1790 IF K1<0 OR J1<0 THEN 1910
1810 IF K1>480 OR J1>480 THEN 1910
1830 K=INT(K1) : J=INT(J1)
1832 Z1(K,J)=Z1(K,J)+1
1836 WRITE #2,K,J,Z1(K,J)
1852 PSET (K,J),2
1853 NEXT N
1858 L=0:GOTO 410
1900 REM N-loop脱出後
1910 FOR LL=0 TO L
1920 X=SX(LL):Y=SY(LL)
1930 KK=(X-CXS)/DX : JJ=(Y-CYS)/DY
1940 IF KK<0 OR JJ<0 THEN 2000
1950 IF KK>480 OR JJ>480 THEN 2000
1960 K=INT(KK) : J=INT(JJ)
1970 '
1974 Z2(K,J)=Z2(K,J)+1
1978 WRITE #3,K,J,Z2(K,J)
1980 PSET (K,J),1
2000 NEXT LL
2010 L=0
2020 GOTO 410
2030 CLOSE
2040 LINE(0,0)-(480,0),0,,2
2050 END

292 マンデルブロ画像の縁(ふち)の画像について。

今まで、各点列を調べる場合に、マンデルブロ集合の縁(ふち)画像を重ね描きしてきた。
この縁周辺の点列が特に面白い画像を生成するから、マウスで始点を選ぶ場合もこの、マンデルブロ集合の縁(ふち)画像の縁を主にクリックして点列を求めた。

***
しかし、この場合、この縁部分(マンデルブロ集合画像の周囲線)は、かなり微妙でその点のとりかたの、わずかな違いで、点列の有無、その形、その種類がまるで違ってくることが分かった。

***
ということで、今回、 マンデルブロ画像の縁(ふち)の画像について見直した。

291 マウスのクリック点での点列画像(その2)

マンデルブロ集合画像の縁(ふち)をマウススでクリックして始点を与えた場合の、『貫通点列』(赤色)と『ブッダブロ点列』(青色]の他の画像例を以下に示す。クリックした点とは全く別の位置に点列が現れる場合がある。







上の画像でも分かるように、マンデルブロ集合画像の『頭部』周辺に『貫通点列』が多く現れることが分かる。この場合でも、『頭部』周辺をクリックして始点にしたにも関わらず、全く別の個所(『腹部』にも同時に点列が現れる。

***
実は、画像の参照として表示したマンデルブロ集合の縁(ふち)は、マンデルブロ集合の真の境界ではない。真の境界よりもが外部の点なのである。現在、調査中であるが、真の境界より少しでも外部に外れた点は、『ブッダブロ点列』となるらしい。また少しでも、真の境界より内部に
ずれた始点のみが『貫通点列』となるらしい
。
***
これは当然なことに思えるが、現在、調査中のプログラム実行結果はこのことを明確に示した結果となっている。

290 マウス・クリックでの点列画像：復習(その1)

ここで少し点列画像の補足説明(復習)をしておこう。
***
複素平面での画像表示座標を適当に選ぶ。
ここでは実軸:-1.5＜X＜0.5,虚軸:-1＜Y＜1とする。
この画像表示座標の一点Zoを任意に選ぶ。

***
ここで、Z(X,Y)←Z(X,Y)^2+Zo の巡回計算を行う。但し、変数:X,Yの初期値はOとしておく。従って巡回の初回計算での右辺は、Z(0,0)^2+Zo=Zo (∵Z(0,0)=0)
従って左辺は、Zoとなる。従って巡回計算初回目で点はZoとなる。

***
次回の計算の右辺は、Z(Zo)^2+Zoとなり、この値が左辺:Z(X,Y)となり、これをZ1で表す。次次回の計算の右辺は、Z(Z1)^2+Zoとなり、この値が左辺となり、これをZ2で表す。この巡回計算を繰り返すと、点列:Zo,Z1,Z2,・・・が得られる。この点列は複素平面上の点列として表せる。

***
この点列において、点の座標原点からの距離:|Z|＞2となった時点で巡回計算を終わらせる。ここで巡回の回数の上限を決めておき、それをNmaxとする。

***
Nmaxまでに、点列の点ZNmaxが|ZNmax|＞2にならないとき、その点列:Zo,Z1,Z2,・・・,ZNmaxを『貫通点列』と名付ける。

***
Nmax以前のNmで点列の点Zmが|Zm|＞2となったとき、巡回計算を終了し、その場合の点列Zo,Z1,Z2,・・・,Zmを『ブッダブロ点列』と名付ける。

***
次に、画像表示座標の他の任意の一点Zoを選んで、上記した計算手順を繰り返せば、
その点Zoに対応した『貫通点列』ないし『ブッダブロ点列』が生成される。

***
下図はマウスをクリックすることで、点Zoを選んだときの『貫通点列』(赤色)と『ブッダブロ点列』(青色)の画像である。点Zoは、マンデルブロ集合の各『こぶ』の縁(ふち)を選んでいる。

















---------------------------------------------------------

『貫通点列』ないし『ブッダブロ点列は、Zoの位置によって大きく変化する。ちょっとクリック点を変えただけで、点列が出たり出なかったりする。出る場合でもちょっとしたクリック点のズレだけで点列の形は大きく変わる。

***
上図でのマンデルブロ集合の上下の対応した『こぶ』で点列を求めたが、それらの点列の形は同一にはならなかった。もしかしたら、厳密に対応点を選べば点列の形は相似になるのかも知れない。しかし、ならないのかも知れない。

***
いずれにしても、マウスでクリックしてZoを選ぶのは厳密さに欠けるが、点列の様子の概要は分かると言えよう。

289 マウスをクリックして始点を選ぶ方法

ブッダブロ点列 (巡回ループを脱出した時点で過去全ての点列)と貫通点列 (巡回ループを脱出できず貫通した時点で過去全ての点列)の画像作成時の始点は、いままで乱数を使うか、あるいは表示座標を全て順次与えていく方法であった。

***
この方法では調べたい点での、それらの点列の様子を調べるには不便であり、始点と、点列の関係もよく分からない。

そこで、あらかじめマンデルブロ集合の縁(ふち)を表示しておき、その縁ないしマンデルブロ集合内部の点を、マウスを使って自由に選び、その点での点列を表示させるプログラムを作った。

***
以下の画像は、そのプログラムによる点列画像である。
表示範囲は実軸:-1.5＜X＜0.5,虚軸:-1＜Y＜1である。最大巡回回数は500とした。
赤色の点列は貫通点列で、青色の点列はブッダブロ点列である。









-----------------------------------------------------------
この方法で分かったことは、マウスでクリックした点とは全く別の座標に点列が
表れる場合が多いということ。

***
当然なことではあるが、マンデルブロ集合部ではブッダブロ点列を生成する始点よりも、貫通点列を生成する始点のほうが圧倒的に多いということ。

そもそも、マンデルブロ画像の内部ないし縁(ふち)は、巡回ループを脱出しない点、ないしは巡ループを脱出するのに巡回回数が無限大となる点の集合だから、ループを貫通してしまうのは当然である。即ち、貫通点列となるのは当然である。

***
しかし、たまにはブッダブロ点列を生成する点もある。比較的に、それが多いのは上図の最後の画像で示しているように、マンデ゛ルブロ集合の『尻』の辺りの点である。理由はよく分からない。

***
参考に、BASIC/98で作った、このプログラムを下記しておく。

10 REM 始点をマウスで入力:マンデルブロ+ブッダブロの点列の表示
90 REM 始点のマウス入力はマウスの左ボタンをクリック。
110 REM 始点の入力の終わりにはキーF1を押す。行82
130 REM 表示座標点→行112,114
150 REM 表示座標→行250,270:変えた場合はマンデルブロ集合画像の縁(ふち)画像も変えること。
190 CONSOLE ,,0,1
210 COLOR 0,7,,,2
230 CLS 3
250 CXS=-1.5:CXE=0.5:DX=(CXE-CXS)/480
270 CYS=-1:CYE=1:DY=(CYE-CYS)/480
290 I=0:II=0:N1=0:NN=0
294 DIM SX(10000):DIM SY(10000)
330 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",350,ALL
350 ON ERROR GOTO 50000
370 REM マンデルブロ集合の縁(ふち)の表示
390 OPEN "C:\BASIC1\TEST\DATAマンデルA.DAT" FOR INPUT AS #1
410 INPUT #1,K,J,C
430 IF EOF(1) THEN 490
450 PSET (K,J),0
470 GOTO 410
490 CLOSE #1
492 ON KEY GOSUB *KEY1
494 KEY(1) ON
500 ON MOUSE(2) GOSUB *M1
510 MOUSE (2) ON
520 '
530 DO:AA=AA:LOOP
540 '
550 *M1
560 A=MOUSE(4,1):B=MOUSE(5,1)
570 CX=CXS+DX*A
580 CY=CYS+DY*B
610 PSET (A,B),2
620 GOSUB 1270
650 RETURN
1270 REM 画像の作成
1290 L=0
1330 K=0:J=0
1410 REM N-loopの計算
1430 X=0:Y=0
1450 FOR N=0 TO 500
1470 XX=X^2-Y^2+CX
1490 Y=2*X*Y+CY
1510 X=XX
1530 Q=X^2+Y^2
1550 SX(L)=X: SY(L)=Y
1570 IF Q>4 THEN 1900
1610 L=L+1
1630 NEXT N
1634 FOR N=0 TO 500
1750 X=SX(N):Y=SY(N)
1770 K1=(X-CXS)/DX : J1=(Y-CYS)/DY
1790 IF K1<0 OR J1<0 THEN 1910
1810 IF K1>480 OR J1>480 THEN 1910
1830 K=INT(K1) : J=INT(J1)
1852 PSET (K,J),2
1853 NEXT N
1858 GOTO 2020
1900 REM N-loop脱出後
1910 FOR LL=0 TO L
1920 X=SX(LL):Y=SY(LL)
1930 KK=(X-CXS)/DX : JJ=(Y-CYS)/DY
1940 IF KK<0 OR JJ<0 THEN 2000
1950 IF KK>480 OR JJ>480 THEN 2000
1960 K=INT(KK) : J=INT(JJ)
1970 C= M MOD 16
1980 PSET (K,J),1
2000 NEXT LL
2010 L=0
2020 RETURN
2030 *KEY1
2040 LINE(0,0)-(480,0),0,,2
2050 END

288 Z^2マンデルブロ集合画像において、巡回ループを貫通する場合の点列の画像

複素画面(実軸:|X|＜2,虚軸:|Y|＜2)の任意の点が与えられると、巡回ループ内で、Z←Z^2+C の巡回計算が行われる。ここで、C は複素平面の任意の点で定数とする。

巡回計算の初期値は、X=0:Y=0であるが巡回するにつれて変化していく。巡回回数の上限を500としたときでも、X^2+Y^2＜4の場合は、そのループを貫通するものとする。

***
このような場合、巡回ループでの点Z(=X+iY)の軌跡はどうなるだろうか？

それを画像化したのが下図である。参照のため、マンデルブロ集合の縁(ふち)も同じ座標で重ね描きしてある。

***
画像結果は、前記事257でのブッダブロー画像と似た画像となった。

巡回ループを脱出できない(つまり、X^2+Y^2＞4 とならない)場合でも特別変わった画像にはならないらしい(但し、画像の形はブッダブローと同様に変化に富んだ画像となっている)。

***
但し、もっとよく調べてみれば、何か特別な規則が見つかるかも知れない。

287 ブッダブロ画像作成時の点列の画像

ブッダブロ画像は、巡回ループを脱出する点Zn(X,Y)があったとき、その点の過去の点、即ち、Z0,Z1,Z2,・・・,Znを全て表示する画像であった。この場合、始点Z0は任意の点として与えられる。

***
以下の図は、画像表示範囲を実軸:|X|＜2,虚軸:|Y|＜2としたとき、任意の始点Z0を500個与えたときの、点列Z0,Z1,Z2,・・・,Znの画像である。参照のため、マンデルブロ集合の縁(ふち)も同一座標で表示している。

***
以下の画像から分かるように、点列が形成されるのは、始点Z0がマンデルブロ集合付近内に限ることが分かる。他の始点の場合は一点Z0で巡回ループを脱出してしまい点列が形成されず、画像の中に孤立した点として残っている。

***
同じ始点から出来る点列は同じ色にしている。但し、色は15色しか使えないから、与える始点の順序をMとすると、色C=M MOD 16としている。

***
点列が形成されるとき、与えられた始点Z0の位置によって、点列の形が
変化している。その形はそれぞれ個性的で面白い。