下図の緑色の集合がZ^2マンデルブロ集合である。

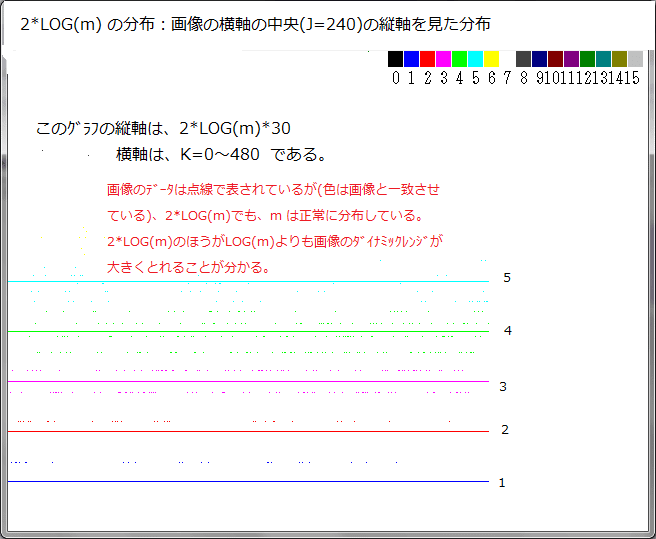
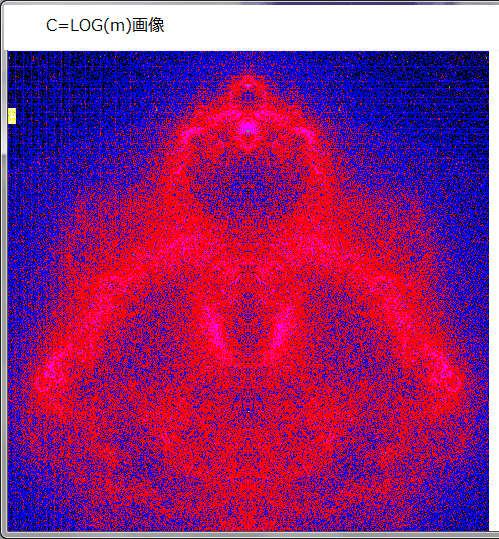
下図は、発散しない点C全てにおける、巡回計算過程での点Z(X,iY)の集合濃度画像である。ここで点Zが同一座標になる場合の回数(濃度)をmとし、BASIC/98での色コードをCCとすると、CC=LOG(m)で表現した。(参考:画像データは下に書いたプログラム1のDATA2に相当する。)
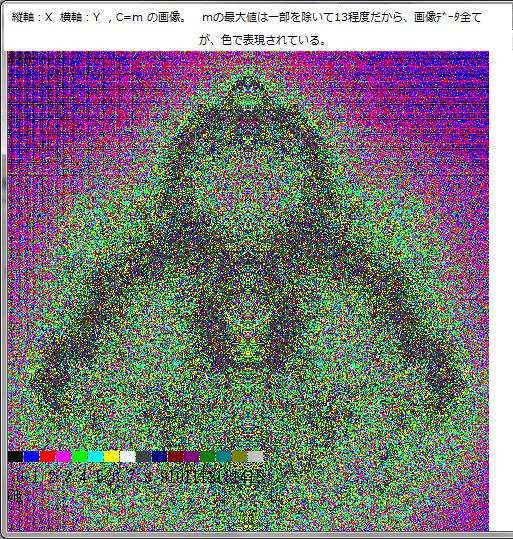
下図の下に、CCの色コードを示してあるから、点(X,iY)が同一座標となる濃度の形態が分かる。例えば、色が緑(CC=5)の場合、その点での濃度は、e^5=148となる。また下図においてマダラに見える黒部分はCC=0故、LOG(m)=0となり、m=1 となる。
但し、m=0 の場合は非表示(空白)とした(参考:下のフログラム3の行511)。
下図の左部分の空白は点(X,iY)が存在しない部分であるが、画像中の白スジ線の存在理由は不明である。

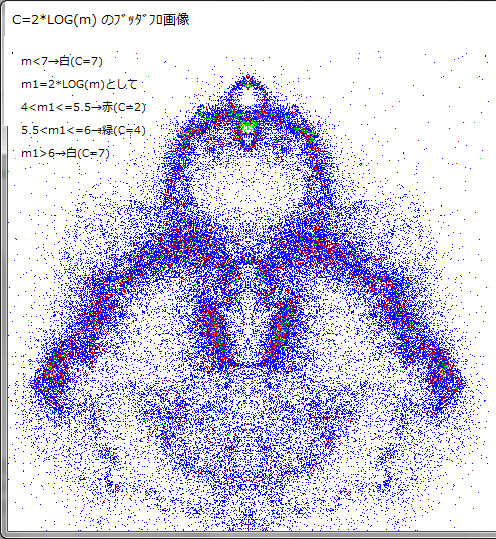
下図は上図に、マンデルブロ集合の境界線(白い線で示した)を重ね描きした画像である。
点(X,iY)の集合は、マンデルブロ集合より、一回り大きく、ぼやけてはいるが外形は似ているのが面白い。マンデルブロ集合の中央部と、左側の「こぶ」あたりに、点(X,iY)の濃度も大きくなっていることが色で分かる。

---------------------------------------------------------------
以下、画像作成のBASIC/98フログラムを示す。基本的に三つのプログラムから構成されている。
・プログラム1→発散しない点C全てにおける、巡回計算過程での点(X,Y)及び当該(K,J)をfile:DATA2に保存する。
10 REM マンデルブロー N-loopの内外保存
12 REM N-loopを脱出したデータ→DATA1
14 REM N-loopを脱出しない全データ→DATA2
16 REM N-LOOPを貫通したデータ→DATA3
20 REM 横軸(K):640 dots、縦軸(J):480 dots
30 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ARCTAN3.BAS",40,ALL
40 CHAIN MERGE "C:\BASIC1\PRO\SUBR\TAN.BAS",50,ALL
50 '
60 CHAIN MERGE "C:\BASIC1\PRO\SUBR\KOSHIKI.BAS",70,ALL
70 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ZFZ.BAS",80,ALL
80 CHAIN MERGE "C:\BASIC1\PRO\SUBR\FGZ.BAS",90,ALL
90 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER1.BAS",100,ALL
100 ON ERROR GOTO 50000
110 CONSOLE ,,0,1
120 COLOR 0,7,,,2
130 CLS 3
140 GOSUB 10000
150 OPEN "C:\BASIC1\RUN\DATA1.DAT" FOR OUTPUT AS #1
152 OPEN "C:\BASIC1\RUN\DATA2.DAT" FOR OUTPUT AS #2
154 OPEN "C:\BASIC1\RUN\DATA3.DAT" FOR OUTPUT AS #3
160 OPEN "C:\BASIC1\RUN\親DATA.DAT" FOR OUTPUT AS #4
170 REM 親DATAの設定(随時変更)
180 CXS=-2.5 :CXE=0.5
190 DX=(CXE-CXS)/640 :DY=DX:CYS=-240*DY
200 WRITE #4,CXS,CXE,CYS,CYE,DX,DY
210 CLOSE #4
220 FOR J=0 TO 480
230 LOCATE 0,0:PRINT J
240 FOR K=0 TO 640
260 CX=CXS+DX*K
270 CY=CYS+DY*J
272 X=0:Y=0
280 FOR N=0 TO 500
290 XX=FNR2(X,Y)+CX
300 Y=FNI2(X,Y)+CY
310 X=XX
320 Q=X^2+Y^2
330 IF Q>4 THEN 380
336 WRITE #2,X,Y,K,J,N
340 NEXT N
342 WRITE #3,X,Y,K,J,N
360 GOTO 420
380 WRITE #1,X,Y,K,J,N
420 NEXT K
430 NEXT J
440 END
・フログラム2→ DATA2の(X,Y)の表示座標系(K,J)への変換し(行170)、同一座標値の濃度を求める(行150~240)。その場合、行200より濃度は+1余計加算されている。また表示座標系(K,J)での各点(X,Y)の最大濃度を求め(行250-300)、file:DAT2Aに保存する(行280)。
10 REM DATA2のX,YのKK,JJ化と、点(KK,JJ)の濃度をZ(KK,JJ)に
12 REM 保存していき、(KK,JJ,Z(KK,JJ))のデータ:DATA2Aを求める。
14 CHAIN MERGE "C:\BASIC1\PRO\SUBR\ER2.BAS",16,ALL
16 ON ERROR GOTO 50000
20 OPEN "C:\BASIC1\TEST\DATA2A.DAT" FOR OUTPUT AS #2
30 OPEN "C:\BASIC1\TEST\DATA2.DAT" FOR INPUT AS #1
40 CONSOLE ,,0,1
50 COLOR 0,7,,,2
60 CLS 3
70 CXS=-2.5:CXE=0.5:DX=(CXE-CXS)/640:DY=DX
80 CYS=-240*DY:CYE=-CYS:M=0
90 DIM Z(640,480)
100 FOR I=0 TO 480
110 FOR II=0 TO 640
120 Z(KK,JJ)=0
130 NEXT II
140 NEXT I
150 INPUT #1,X,Y,K,J,N
160 IF EOF(1) THEN 242
170 KKK=(X-CXS)/DX: JJJ=(Y-CYS)/DY
180 KK=INT(KKK):JJ=INT(JJJ)
190 IF KK>640 OR JJ>480 THEN 240
191 IF KK<0 OR JJ<0 THEN 240
200 Z(KK,JJ)=Z(KK,JJ)+1
202 C=Z(KK,JJ) MOD 16:PSET(KK,JJ),C
212 M=M+1:LOCATE 0,0:PRINT M
240 GOTO 150
242 CLS 3
250 REM KK,JJ,Z(KK,JJ)の保存→DATA*A
260 FOR JJJ=0 TO 480
270 FOR KKK=0 TO 640
271 IF Z(KKK,JJJ)=0 THEN 290
280 WRITE #2,KKK,JJJ,Z(KKK,JJJ)
282 CC=Z(KKK,JJJ) MOD 16:PSET (KKK,JJJ),CC
290 NEXT KKK
300 NEXT JJJ
410 END
・フログラム3 →DATA2A(濃度データ)の表示。
10 REM 画像表示
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR左下表示.BAS",55,ALL
55 OPEN "C:\BASIC1\RUN\DATA2A.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
80 REM Zによる色の区別:サブルーチン
90 GOSUB 500
100 PSET (K,J),C
110 GOTO 60
120 CLOSE #1
130 GOTO 600
500 REM Zによる色の区別:最初からZは1加算されているから補正をする
510 Z=Z-1
511 IF Z=0 THEN 550
520 C=LOG(Z)
550 RETURN
600 GOSUB 3000
610 END
・フログラム4 →画像表示及びマンデルブロ集合の境界線の表示
10 REM 画像表示及びマンデルブロ集合の境界線の表示
30 CONSOLE ,,0,1
40 COLOR 0,7,,,2
50 CLS 3
51 CHAIN MERGE "C:\BASIC1\PRO\SUBR\COLOR左下表示.BAS",52,ALL
55 OPEN "C:\BASIC1\RUN\DATA2A.DAT" FOR INPUT AS #1
60 INPUT #1,K,J,Z
62 LOCATE 0,0:PRINT USING "###";J
64 LOCATE 0,1:PRINT USING "###";K
70 IF EOF(1) THEN 120
80 REM Zによる色の区別:サブルーチン
90 GOSUB 500
100 PSET (K,J),C
110 GOTO 60
120 CLOSE #1
130 GOTO 600
500 REM Zによる色の区別:最初からZは1加算されているから補正をする
510 Z=Z-1
511 IF Z=0 THEN 550
520 C=LOG(Z)
550 RETURN
600 GOSUB 3000
610 REM 旧data1からマンデルブロ画像の境界付近の画像の読み込み
620 OPEN "C:\BASIC1\RUN\DATAmandel.DAT" FOR INPUT AS #1
630 INPUT #1,K,J,N
640 IF EOF(1) THEN 670
650 PSET (K,J),0
660 GOTO 630
670 CLOSE
680 END