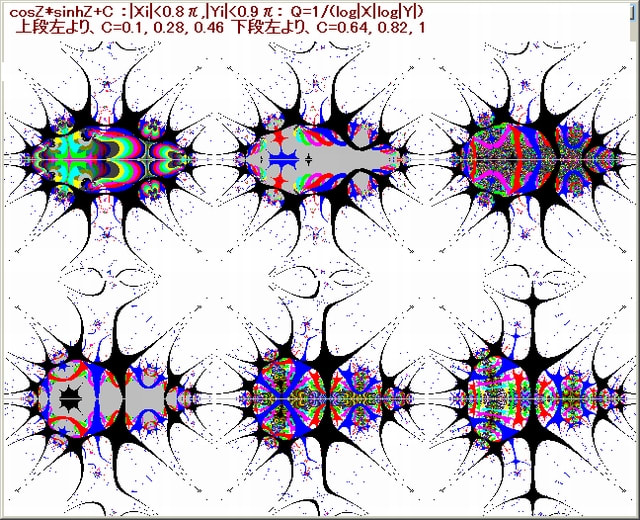
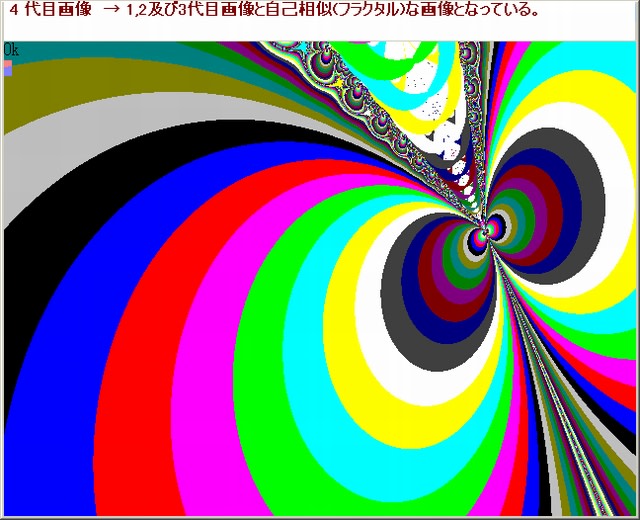
今回の画像は前の記事(122)での画像:Z^5+0.53616 の中の 4 箇所の部分を拡大して見る。
下図は前の記事(122)での画像:Z^5+0.53616 である。

---------------------------------------


---------------------------------------




-----------------------------------------
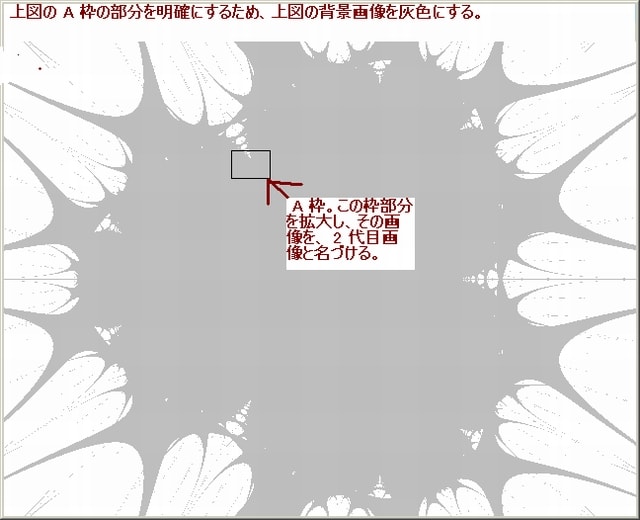
上図(A,B,C)の中央あたりに在る円状の黒い部分は、N-loopを貫通してしまうような座標 (Xi,Yi)点の集合である。ここで、Nmax=500→1000 に変えた場合の A 画像が下図である。

上図から分かるように「中央あたりに在る円状の黒い部分」は小さくなっている。即ち、Nmaxを増加したためN-loopを貫通せず脱出するような座標 (Xi,Yi)点が増加していることを意味している。換言すれば、N-loopを貫通するような座標 (Xi,Yi)点が減少していることを意味している。
当然、Nmax を更に増加すれば「中央あたりに在る円状の黒い部分」は更に小さくなっていくだろう。
おそらく、Nmax→無限大にすると「中央あたりに在る円状の黒い部分」は或る1点に収束していくと思われる。そういう意味での特異点が「中央あたりに在る円状の黒い部分」に存在すると思われる。そういう特異点は、画像:Z^5+0.53616 には何個存在するのか? これも興味ある問題である。